金属中纵向电磁振荡的特性及其在平面和球面的激发

背景

飞秒激光脉冲照射平面金属表面通常会形成激光诱导的周期性表面结构 (LIPSS) [1]。除了 LIPSS，还观察到称为高空间频率 LIPSS (HSFL) 的超精细波纹 [1, 2]。 HSFL的空间周期明显小于照射波长λ 0. 例如，对于铝，这个周期估计在 λ 处为 20 到 200 nm 0=0.8 μ 米 [2, 3]。虽然普通 LIPSS 中波纹的方向垂直于激光偏振，但 HSFL 的方向通常垂直，有时平行于偏振。在透明电介质、半导体和金属的表面上形成了类似的 HSFL。 HSFL的起源可以用不同的机制来解释，例如二次谐波的产生、特定类型等离子体模式的参与、自组织以及介电材料非均匀击穿过程中的局部场增强[2, 3]。

本研究的目的是寻找一种可以产生短周期Λ形态的波动过程 ≪λ 0. 我们研究了金属中纵向 (L) 电磁波的特性，也称为等离子体波。我们的研究包括以下新步骤。首先，我们从定义介电常数的空间分散开始我们的研究。如下所示，如果所研究的介质不是均匀和无限的，那么通用定义是没有用的。因此，我们提出了空间色散介电函数ε的新概念 .此函数建立两个向量场之间的正比例关系，E (r ,ω ) 和 D (r ,ω )，但不是振幅 E (k ,ω ) 和 D (k ,ω ) 的平面波。因此，量 ε 取决于波数的平方，k ² ，电场矢量亥姆霍兹方程的参数E (r ,ω )，但不是波矢量 k 的平面波。然后，为了推导出这样一个新颖的函数，我们通过求解以弛豫时间近似编写的玻尔兹曼传输方程来确定传导电子对电磁模式的响应。获得了所谓的横向和纵向 Lindhard 介电函数。此外，我们发现纵向 Lindhard 和更简单的流体动力学函数在很宽的参数范围内都很接近。为了说明该理论，考虑了银和金纳米球的消光。我们首次证明非局域 Mie 理论解释了随着贵金属纳米球尺寸减小而观察到的等离子体共振的蓝移、展宽和最终消失。最后，应用新开发的理论模型来检验纵模参与激光诱导表面结构形成的可能性。为此，我们在考虑透射纵波的情况下修改了菲涅耳理论。

方法

为了确定分段均匀介质中的电磁场，应用了经典电磁理论。电场E 在异质介质的每个均匀域中，假设为向量亥姆霍兹方程 (VHE) 的解：

其中Δ 是拉普拉斯算子。

像往常一样，电 E 的切向分量 和磁性 H 跨媒体边界的领域是连续的。此外，我们考虑到电子被限制在金属中；因此，电流密度的法向分量 j 的以下附加边界条件 (ABC) 在金属表面S 被使用：(j n )| r ∈S =0。

为了确定金属中的传导电流，我们求解了以弛豫时间近似表示的玻尔兹曼传输方程 (BTE)：

其中 f 是相空间中的单粒子分布函数 (r , v ), v 是微观电子速度，e 和 m 分别是电子电荷和质量，B 是磁感应强度，f 0 是均衡分布函数，τ 是放松时间。

下面，我们推导出空间色散介电函数的公式。然后，我们用它们来研究平面金属表面的光反射和贵金属纳米球上的光散射。

结果与讨论

ε 的空间离散 在异质介质中

在文献中，空间色散介电函数ε 通过以下关系[4-6]定义：

其中 ε 0 是电常数，D (ω , r ) 是角频率 ω 的位移矢量振荡幅度 在 r 点 , 和 E (ω , r ^′ ) r 点的电场振荡幅度 ^′ .等式的傅立叶变换。 (3) 给出方程

其中空间分散的 ε (ω , k ) 取决于波矢量 k 平面电磁波。在我们看来，方程。 (3) 不仅在无限同质体积中是模糊的，而且我们处理分段异构系统，其中应考虑边界和 k 在不同的媒体中是不一样的。

我们的方法不使用电磁波在平面波上的扩展。空间色散介电常数决定了 D 之间的关系 (ω , r ) 和向量亥姆霍兹方程的特殊解。 (1)：

这里E (ω , r ) 表示电场的分布，而不仅仅是矢量 E 在 r 点 .

纵向和横向介电函数

金属的介电常数通常用电导率 σ 表示 [4]：

其中 ε g 是允许固体极化的介电函数的一部分； ε 对于简单金属，g=1。为了确定σ ，我们计算了电流密度

其中 \(\mathrm {d} \mathbf {v}=\frac {v}{m}\,\mathrm {d} \epsilon \,\mathrm {d}\,\Omega,\) d​​ Ω =sinθ dθ dφ , v , θ , φ 是速度的球坐标。与以往的研究不同，我们没有引入波矢k 但找到了包含运算符 v 的无限级数形式的 BTE 解决方案 ∇ 作用于 v E ：

其中 Γ =1/τ .然后，f 0 由零温度费米-狄拉克分布逼近，并且经过 ε 积分后 在方程式中(7)，我们得到了

其中 \(\omega _{\mathrm {p}}^{2}=\frac {e^{2}\,n_{e}}{m\,\varepsilon _{0}},\) ω p 是等离子体频率，\(\mathbf {u}=\frac {\mathbf {v}}{v}\) 是 v 方向的单位向量 ,\(l=\frac {v_{\mathrm {F}}}{-i \omega +\Gamma },\) v F 是费米速度。进一步，我们计算了积分

其中 n 是一个自然数。 j的以下依赖 在任意 电场 E 终于得到了

方程有两种解。 (1)、满足方程∇的无散度 ·E =0 且无旋转满足方程

对于平面波，E ∝ exp[i (k r -ω t )]，等式。 (14) 转化为关系k ×E =0 表示波是纵向的（L）。为了模拟球体中的过程，使用矢量球谐函数 L 很方便 , M , 和 N 作为一组完整的正交函数。在这种情况下，方程。 (14) 指定谐波L . L波和L的波数 模式由以下色散定律确定

从方程。 （6）和（13）我们发现方程的解。 (1) 满足方程的约束。 (14) 给出以下纵向介电常数

其中 Φ 是 Lerch 的 Phi 函数，

\(a=\frac {k v_{\mathrm {F}}}{\omega +i \Gamma }\).

获得的介电常数与 Kliewer 和 Fuchs [7] 定义的介电常数不同，仅在符号上：

身份

允许重写方程。 (18)如下

在Γ的情况下 =0，该公式采用 Klimontovich 和 Silin [8] 推导出的方程的形式，他们研究了退化血浆中的 Landau 倾倒（参见 [9]、[10，方程 (40.17)] 和 [11]）。等效方程的介电常数。 (16), (18), (20) 通常被称为 Lindhard 介电函数（参考 [12]），尽管该函数最初由 Klimontovich 和 Silin [8] 得到。

横向 Lindhard 介电常数 [7] 可以通过方程找到。 (13) 当∇ ·E =0。在 v 的实际情况中 F k ≪ω ，它降低到德鲁德介电函数

该函数与许多金属的实验数据一致 [13]。如果 |a |<1，纵向介电常数(16)简化为流体力学介电函数：

平面电磁波从平坦金属表面的反射

边界条件

在本节中，我们确定波矢k的方向 ^L 平面电磁波从平坦金属表面反射时在金属中激发的L波的幅度和幅度。

考虑平面波入射在电介质-金属界面z =0，波矢位于 xz 飞机。电介质 1 中的电场由入射 E i 和反射 E r 波，金属 2 中的场具有透射横向 E t，在某些情况下，纵向 E ^L 组件。根据麦克斯韦边界条件，电场矢量和磁场矢量的横向分量在平面z上是连续的 =0。此外，电子不会从金属中射出；因此，电流密度的法向分量在 z 处为零 =0,

\(\hat {\mathbf {z}}\) 是 z 方向的单位向量 轴。

麦克斯韦边界条件中的所有项必须对 x 具有相同的依赖性 和 y .这个要求有几个后果。首先，可以确定当入射波的电矢量 E ^{(i )} 平行于入射平面。换句话说，等离子体激元可以由横向磁 (TM) 波产生。效果与金属球体中的效果非常相似 [14]。其次，可以从条件推导出类似于斯涅尔定律的公式

其中索引 1x 和 2x 表示 x - 媒体 1 和媒体 2 中向量的投影，分别为 θ 1为入射角。

反射和透射系数

让我们确定入射在平面金属表面上的平面 p 极化电磁波形成的场。用x表示电场和磁场的分量很方便 E 的组件 ^{(i )} ，即 E x (r)=− r E x (i) 对于反射波，E x (t)=t E x (i) 对于透射横波，和

对于传输的纵波，这里 r 是反射系数，t 和 t L为传输系数。

从麦克斯韦边界条件和方程的ABC。 (23) 写成如下形式

我们得到了

在 δ =0，系数r 成为 p 偏振波的菲涅耳反射系数（例如，参见 [4] 的方程 (2.49)）。在相同条件下，t 不是菲涅尔传输系数，因为我们定义了 t 和 r 与菲涅耳的不同。

金属纳米球灭光

在之前的一篇论文中，其中一位作者概括了洛伦兹-米理论，允许方程的 ABC。 (23)。菲涅耳系数的模拟 r , 米氏系数 b l 对于 l 的反射 TM 模式 发现第 1 个订单是

哪里

ψ l 和 ζ l 是 l 阶的 Riccati-Bessel 和 Riccati-Hankel 函数 ， 分别; j l 是球面贝塞尔函数，素数表示函数对其自变量的导数。

让我们将经典和广义 Lorentz-Mie 理论的预测与实验数据进行比较。在 [15] 中，Hilger、Tenfelde 和 Kreibig 研究了沉积在电介质表面上的银纳米粒子的消光光谱。在研究的第一阶段，研究人员生成平均直径为 2、3.5 和 4 nm 的银粒子束，确定其中一个光束的粒径分布，记录消光光谱，并估计参数 A 现象学公式Γ的=0.25 =Γ b+A v F/R , 其中 Γ b 是体金属弛豫率，对于真空中的银球。首先，我们计算了一束平均直径<D的银球的消光光谱 〉=2 nm 和实验尺寸分布从 D 跨越区域 =1 到 D =4 纳米。我们的理论不包含可调参数。为了定义介电函数，我们使用了 Lynch 和 Hunter [16] 提出的块状银的折射率列表（见图 1）。我们还应用了方程。 (16)、(21) 和 (22) 与 ω p=9.17 eV，Γ b=0.021 eV，v F=1.39×10 ⁶ 米/秒，和A =0.25。计算结果和实验光谱如图2所示。

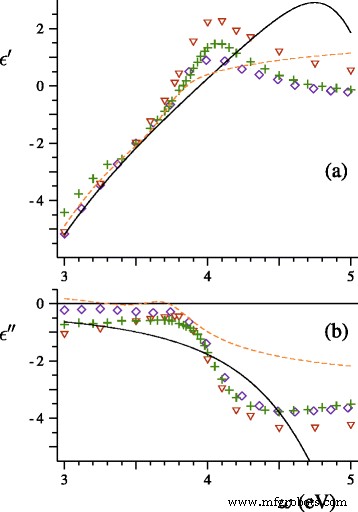
真实 (a ) 和虚数 (b ) 根据 Johnson 和 Christy (◇) [20]、Lynch 和 Hunter (+) [16]、Weber (△) [21]、Hao 和 Nordlander（虚线 ) [22] 和 Drachev 等人。 （实线 ) [23]

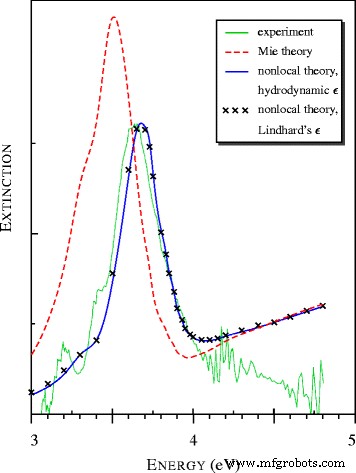
在 [15] 中观察到的银纳米级粒子消光光谱，并使用局部和非局部模型计算。所有理论光谱均以共同的相对单位表示

图 2 中的理论光谱是使用 Klimontovich-Silin-Lindhard 和更简单的流体动力介电函数计算的。令人惊讶的是，即使 |a |>1 在等离子体共振区域。

对于纳米尺寸的银球，消光光谱中的最大值，称为 Fröhlich [17]、等离子体和表面等离子体极化子 (SPP) [15] 共振，已知从 3.5 到 3.65 eV [18]。非局部模型与实验数据非常吻合，而局部 (Mie) 理论在 ω 处给出最大值 ≃3.5 eV（见图2和表1）。

以下考虑可以支持等离子体共振蓝移的计算。在静电近似中，只有 b 1 有助于消光截面 Q 分机和等式。 (30) 可以通过使用以下近似值来简化

因此，Q ext 在

获得的条件（33）考虑了 L 的激发 模式（根据术语 δ 1) 因此，不同于 Fröhlich 共振条件 [17]：。

在实验[15]中，峰值频率ω m和共振宽度Δ ω 的消光光谱几乎独立于<D 〉。 Δ的这个特点 ω 似乎不同意经典的米氏理论。实际上，局部理论预测等离子体共振会随着 D 的减小而变宽 （在 A =0.25)，如表 1 所示。同时，非局域理论给出了近似相等的共振宽度，但峰值位置不同。来自所有粒子的贡献的叠加给出了Δ的值 ω 与实验数据非常吻合。有趣的是，非局域理论预测即使在 A 光束的等离子体共振也会变宽 =0。

在 ω> 4 eV，图 2 中平滑的理论曲线高于狭窄的紧密定位的实验峰的混合物。如图 1 所示，带间吸收在该光谱范围内占主导地位。观察到的光谱特性很可能是从连续谱带过渡到离散能级结构的结果。这种量子尺寸效应是在金纳米球的光学特性研究中发现的 [19]。当银球尺寸增加到<D 〉=3.5 nm，吸收首先相对于最大值增加，并形成一系列小的等距下降的平台。然后，吸收在<D处略有下降 〉=4 纳米。

为了研究等离子体共振蓝翼的形成，我们计算了超锡银粒子的消光光谱并将它们呈现在图 3 中。图 3 中的一个显着特征是等离子体共振在 <我>D =1 纳米。早些时候，在金纳米球的实验研究中观察到了这种效应[19]。特别是，在[19]的图9中，将直径为1.7、1.9、2.0、2.1、2.3和2.5纳米的粒子的实验光谱与局部米氏理论计算的光谱进行了比较。该协议很差，未能描述等离子体共振的扩大及其位置 [19]。通过改变粒子的尺寸和介电函数的修改来改善拟合的尝试并没有成功。根据 [19] 的作者，观察到的异常宽或压抑的集体振荡带抵抗与局部 Mie 理论的建议修正相吻合。从图 4 可以看出，如果应用非局部 Mie 理论，情况会发生巨大变化。请注意，我们没有使用可调整的参数。 Johnson 和 Christy [20] 的复折射率表格用于确定金的介电函数。其他参数，包括 A =1，甲苯的折射率（1.37）取自[19]。

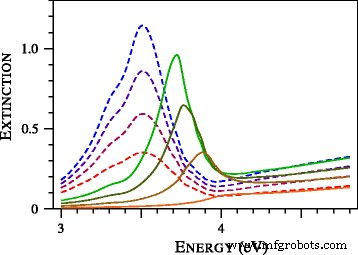
用局部（虚线 ) 和非局部（实线 ) 米氏理论。颗粒越小，曲线越低。所有理论截面均以通用的相对单位表示

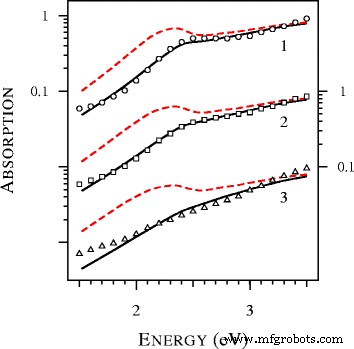
用局部（虚线 ) 和非局部（实线 ) 米氏理论和实验数据 (点 ) 从 [19] 的图 9 中提取，用于具有 D 的金球 =2.5、2.1 和 1.7 nm，在甲苯中（曲线 1 和 圆圈 , 曲线 2 和 平方 , 以及曲线 3 和 三角形 ， 分别）。所有理论光谱均归一化为 4.12 eV 并垂直位移

纵波的波数

纵向模式与横向模式的不同之处在于波数要高得多。例如，对于图 2 所示的计算，\(k_{2}^{\mathrm {L}}\) 的实部对应于空间周期 \(\Lambda =2 \pi /\Re k_{ 2}^{\mathrm {L}}\) 在 ω 处从 9 nm 减小到 2 nm 从 3 eV 增加到 4 eV。在这个ω 区间，比值 \(k_{2}^{\mathrm {L}}/k_{2}\) 的绝对值从 130 减小到 100，参数 δ 等式的(27) 在 θ 从 0.01 下降到 0.005 1=π /4。因此，我们得出结论，在平坦的银表面上 L 波的激发可以忽略不计。然而，L 已发现模式在纳米尺寸的银团簇中很重要。

替换方程中的术语 \(-\,\omega ^{2}_{\mathrm {p}}/(\omega ^{2}+i \Gamma \omega)\)。 (16) 由 ε ^T -ε g 根据方程。 (21) 允许我们重写色散方程。 (15) 如下形式

在 ε 的最简单情况下 g=1 和 Γ =0，方程(35) 预测金属对于 ω 处的横波和 L 波都是透明的>ω p 但都是 k ^L 和 k ^T 在 ω 处复数 <ω

如果固体是透明的，则在平面上的 p 偏振波斜入射下可以激发纵波。这种效果有几个明显的特点。首先，纵波可以在平坦的表面上产生，而应该特别努力地激发表面等离子体激元 [4, 5]。其次，在干涉图中，电磁场强度不是沿着界面而是垂直于界面调制。因此，由于固体的散裂，空隙可能出现在平行于表面的平面中。根据ω的定义 p，条件ω>ω p 可以在具有低载流子密度的固体（例如，半导体）中遇到。我们在这里不检查这种情况，因为 ε 的公式 ^L 由简并电子气导出。

结论

为了定义空间相关的介电函数，之前所有的研究人员都考虑了物质与平面电磁波的相互作用。当场位于腔内并且必须以某种方式考虑边界条件时，这种方法在纳米光学中不具有建设性和严格性。我们通过计算介质对满足向量亥姆霍兹方程的电场的响应来解决这个问题。导出的空间色散介电函数取决于波数的平方，这是亥姆霍兹方程的一个参数，而不是平面波的波矢。

我们报告了由于金属中纵波的激发而修改的菲涅耳反射系数。之前对 Mie 系数进行了类似的概括。在此，该理论已通过纳米尺寸的银和金簇的消光模拟得到验证。计算出的从 3.5 到 3.65 eV 的偏移和银粒子束的表面等离子体共振宽度与实验数据非常吻合。此外，非局域模型解释了直径约 2 nm 的金色球体的等离子体共振消失。重要的是，平面入射波可以在平面上激发 L 波。这是等离激元与表面等离激元的主要区别。

The properties of the electromagnetic oscillations in metals have been examined. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.