具有自旋相关点间耦合的三量子点中的自旋极化输运和自旋塞贝克效应

介绍

随着自旋电子学 [1-3] 的发展，自旋热电子学 [4, 5] 在过去的二十年中受到了广泛的关注。在自旋电子学中，最吸引人的问题之一是通过电偏压控制电子自旋。而在自旋热电子学中，自旋控制方法主要是热偏置，即施加在系统不同端之间的温度梯度。它被认为是自旋电子学和热电学的结合。特别令人感兴趣的是自旋塞贝克效应 (SSE)，它产生纯自旋电流，而没有电荷对应物的伴随，或以自旋向上和自旋向下化学势分裂为特征的自旋偏压。它开辟了一种利用纳米结构中产生的多余热量来降低能耗并提高热器件性能的方法。这种装置在利用载流子自旋自由度检测系统温度梯度方面也很有效。自 2008 年以来，K. Uchida 等人不断报道了 SSE 观测的一些重大实验突破。在磁性金属 [6]、铁磁绝缘体 [7, 8] 和铁磁金属 [9] 中。随后在铁磁半导体 [10]、具有磁场的非磁性材料 [11]、顺磁材料 [12]、反铁磁材料 [13]、金属-铁磁绝缘体界面 [14] 以及拓扑绝缘体 [15-17] 中进行了研究].

Mahan 和他的同事证明，在低维系统中常见的类似三角形的传输函数形状将显着提高热电设备的效率 [18]。从那时起，零维量子点 (QD) [19, 20] 中载流子被限制在所有三个维度已被广泛研究以提高 SSE 系数（自旋热电势），这表明在由无限小的热偏置引起的开路条件 [4-6]。特别是，如果系统中存在多个传输路径，电子之间会相互干扰，并可能产生有趣的 Dick [21, 22] 或 Fano [23, 24] 效应，其特征是传输函数和电导发生急剧变化.因此，大量工作致力于研究包含 QD 的各种环形或多路径结构中的 SSE [25-33]。其中丰富的参数，如可调点能级、库仑相互作用、磁通量、自旋轨​​道相互作用、点-引线耦合的不对称性等，可以有效控制量子干涉过程，产生巨大的自旋热电势，其幅度可达高于甚至高于充电的。

已经在实验和理论中制备了各种形状的三重量子点 (TQD)，重点是稳定性图、电荷整流、电荷挫败、量子干涉效应和相干自旋控制 [34-46]。其中，由于量子干涉效应的存在，以环形连接的点更有趣[39-46]。与电子传输相比，热电效应，尤其是 SSE 在 TQD 中很少被研究。在本文中，我们研究了 TQD 中的 SSE，同时考虑了自旋相关的点间耦合（见图 1）。通过在 QD 之间的隧道结上施加静态磁场，电子自旋执行拉莫尔进动，并且点间耦合变得依赖于自旋 [47, 48]。最近，还提出通过利用振荡磁场和时间控制的栅极电压，可以将不同自旋分量的电子波函数分离到不同的 QD 中，从而产生自旋分辨的传输速度（耦合强度）[49, 50]。在之前的一些工作中，已经研究了自旋相关的点间耦合对自旋电流产生的影响 [51, 52]。在这里，我们表明它可以通过改变 Fano 反共振状态将自旋向上和自旋向下热电势的位置移动到点级空间中的相反方向，导致 100 % 自旋极化或纯自旋热电势，其大小可以与电荷一一样大。这种效果与自旋无关的点间耦合的情况完全不同 [53, 54]。有趣的是，获得的结果可以通过点间耦合的非常小的自旋极化来实现。

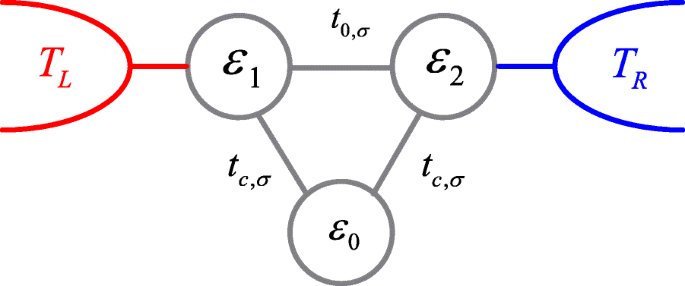
三重量子点系统的示意图。通过在点之间的隧道势垒上施加静磁场，点间耦合变得依赖于自旋

模型和方法

图 1 中连接到两条引线的 TQD 的哈密顿量可以通过以下安德森哈密顿量进行建模 [25, 33, 51, 52]，

其中 \(c_{k\beta \sigma }^{\dag } \left (c_{k\beta \sigma }\right)\) 与 β =L ,R 和 \(d_{i\sigma }^{\dag } \left (d_{i\sigma }\right)\) 与 i =0,1,2分别是lead-β中的创生（湮灭）算子 和点-i 自旋 σ .我们假设每个点都包含一个能级 ε 我 并忽略点中电子与引线之间的库仑相互作用。 QD-1 和 QD-2 通过点间耦合 t 相互耦合 0,σ =t 0(1+σ p ) 并通过点引线耦合 V 连接到左右引线 千升 和 V kR ， 分别。 QD-0 以 t 强度连接到 QD-1 和 QD-2 c ,σ =t c (1+σ p )，其中 σ =±1 分别为自旋向上和自旋向下的电子。

在线性响应范围内，我们可以在无限小的电位差Δ下单独写出与自旋相关的电流和热电流 V 和温差Δ T 左右引线之间为 [25, 33]

其中 e 是电子电荷和 T 系统平衡温度。系数K n ,σ 上式中由 [25, 33]

其中 \(\hbar \) 是约化的普朗克常数，μ 引线的化学势，f (ε ,μ )=1/{1+exp[(ε -μ )/k B T ]} 具有玻尔兹曼常数 k 的费米分布函数 B .

在方程式中。 (4)、透射系数T σ (ε ) 对于每个自旋分量可以根据延迟格林函数获得 [25, 33] \(T_{\sigma }(\varepsilon)=\Gamma _{L}\Gamma _{R} \left |G_{ 21,\sigma }^{r}(\varepsilon)\right |^{2}\)，其中\(\Gamma _{L(R)}=2\pi \sum _{k}|V_{kL( R)}|^{2}\delta \left [\varepsilon -\varepsilon _{kL(R)}\right ]\) 是线宽函数。应用运动方程方法，我们可以很容易地推导出 \(G_{21,\sigma }^{r}(\varepsilon)\) 的解析形式为 [55, 56]

其中 \(\tilde {\varepsilon }_{1(2)}=\varepsilon -\varepsilon _{1(2)}+i\Gamma _{L(R)}/2\)。则透射系数为 [55, 56]

每个自旋分量 S 的热电势（塞贝克系数） σ 在充电电流为零的情况下计算J e =J e ,↑ +J e ,↓ =0，由 [25, 33] S 给出 σ =-K 1,σ /(e T K 0,σ )，电荷（自旋）热电势由 S 给出 c (s )=S ↑ +(-)S ↓ .

结果和讨论

在下面的数值计算中，我们选择线宽函数Γ L =Γ R =Γ 0=1 作为能量单位并固定μ =0 作为能量零点。 e 的常数 , k B , 和 h 都设置为 1。图 2 显示了自旋相关的电导 G σ 和热电S σ 作为点级别 ε 的函数 0=ε 1=ε 2 对于 t 0=0，即 TQD 串联。当点间耦合独立于自旋 (p =0)，(a) 和 (b) 中的自旋向上和自旋向下电导相同，并在 ε 处形成一个峰 0=0（黑色实线）。

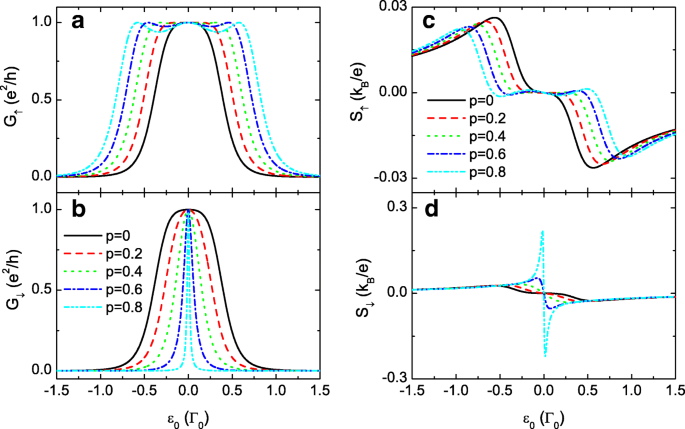
t 的电导和热电势 0=0。自旋极化电导G σ 在 a 和 b , 和热电 S σ 在 c 和 d 作为点级别 ε 的函数 0 表示固定 t 0=0 和点间耦合的自旋极化的不同值。其他参数是电平失谐Δ =0，温度T =0.001 和 t c =0.3

在存在自旋相关的点间耦合 p ≠0，自旋电导G的单峰 ↑ 由于增强的自旋向上点间耦合 t，图 2a 中的三峰构型演变为最大峰值不变的三峰构型 c ,↑ .而 G ↓ 由于 t 较小，保留了峰宽减小的单峰模式 c ,↓ .对于 t 0,σ =0 和相同的量子点水平 (ε 1=ε 2=ε 0)，方程中的传输系数。 (6) 减少到

传递函数中存在三个共振，分别位于ε =ε 0 和 \(\varepsilon =\varepsilon _{0}\pm \sqrt {2t_{c,\sigma }^{2}+\Gamma _{0}^{2}/4}\)。在低温条件下，ε处的电导出现三个共振峰 0=μ 和 \(\varepsilon _{0}=\mu \pm \sqrt {2t_{c,\sigma }^{2}+\Gamma _{0}^{2}/4}\) 分别。对于弱点间耦合的情况，三个峰合并为单峰配置，如图 2a 和图 2a 中的黑线所示。随着点间自旋极化p的增加 , t 的值 c ,↑ =t c (1+p ) 增加并且自旋电导的三个峰值在能量空间中分离，如图 2a 所示。同时，t的幅度 c ,↓ 变得更小和 G ↓ 在图 2b 中相应地保持单峰模式。从方程。 (6) 还可以看到峰宽随着t的减小而减小 c ,↓ .

当 p =0，图 2c 和 d 中每个自旋分量的热电势均相同且反对称于电子-空穴对称点 (ε 0=0)，这与之前的工作一致 [33, 57]。由于产生热电效应的温度梯度的存在，左边引线的温度高于右边引线的温度，化学势μ以上的电子较多 在左边领先。相应地，μ下方有更多的孔洞 .当量子点的能级低于（高于）μ ，主要载流子是空穴（电子），然后热电势为正（负）[57]。热电势在 ε 处改变符号 由于电子和空穴的补偿，0=0。随着 p 的增加 , 自旋热电的峰宽 S ↑ 随着峰值的减小而放大。而降速的范围缩小了。有趣的是，S 的峰值 ↓ 通过增加 p 明显增强 .对于大点间自旋极化的情况，例如p =0.8，S的峰值 ↓ 大约是 S 的十倍 ↑ 与自旋相关的电导值几乎没有变化 G σ .这可以解释如下。对于正 p , 点间隧穿率 t c ,↑>t c ,↓ 并且自旋向上的电子（或空穴）将比自旋向下的电子更快地通过 QD。相应地，与自旋向上的电子（空穴）相比，在左（右）引线处被阻挡的自旋向下电子（空穴）更多，导致响应温度梯度的自旋向下电压更大。

进一步放大S之间的差异 ↓ 和 S ↑ ，我们展示了极大p的结果 在图 3. 我们发现自旋电导 G ↑ 和热电S ↓ 受p变化的影响较小 ，如图 3a 和 b 中的插图所示，用于比较。随着 p 的增加 ，自旋下降的载流子变得更难通过 QD 传输，并将在引线上累积。因此，G 的值 ↓ 被单调抑制，但 S 的峰值 ↓ 显着扩大，表明通过依赖于自旋的点间耦合产生完全自旋极化的热电势的有效手段。该结果也有望用于通过 SSE 技术检测系统中的温度梯度。既然弱点间耦合增强了热电势值，那么我们选择较小的 t c 固定 p =0.7 in Fig. 4. 在这种情况下，自旋向上和自旋向下电导中的三个共振峰合二为一。电导的峰宽随着t的增加而变宽 c 这与之前的结果一致。图 4b 和 d 显示 S ↑ 和 S ↓ 通过减少 t 来增强 c .降速热电的最大值也可以达到约4 k B /e 对于 t c =0.02Γ 0. 在实验中，点间耦合可通过栅极电压或隧道势垒的厚度进行调节。因此，通过改变t来提高热电势可能更可行 c 具有固定的自旋极化 p ，因为与电场相比，磁场通常更难以控制。事实上，可以用很小的 p 获得大的热电势 在某些条件下，如下所示。

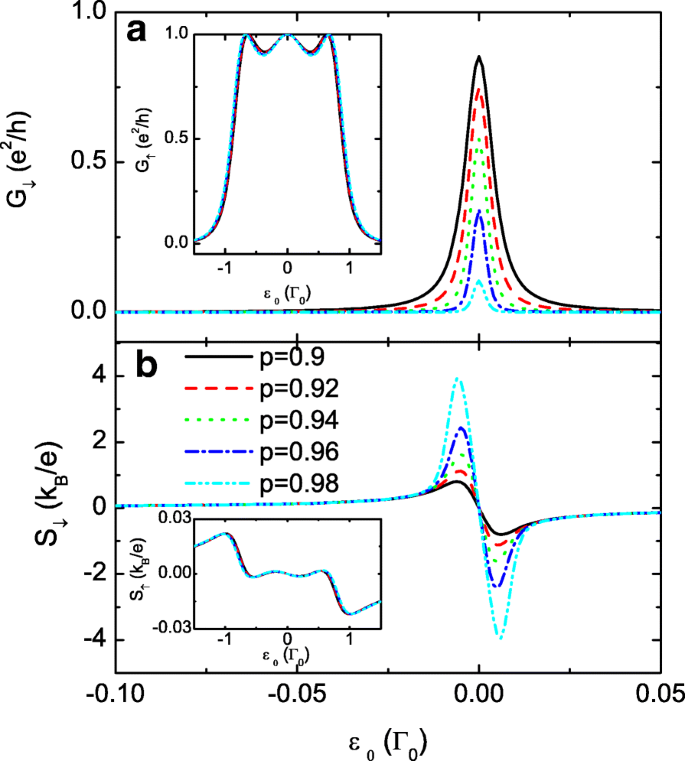
降速电导和热电势。自旋向下电导G ↓ 在 a 和热电 S ↓ 在 b 对于大点间耦合的情况 1>p ≥0.9。 a 中的插图 用于 G ↑ 在一个大点级制度中，以及 b 中的插图 表示与自旋向下的热电势相比，自旋向上的热电势。其他参数如图2

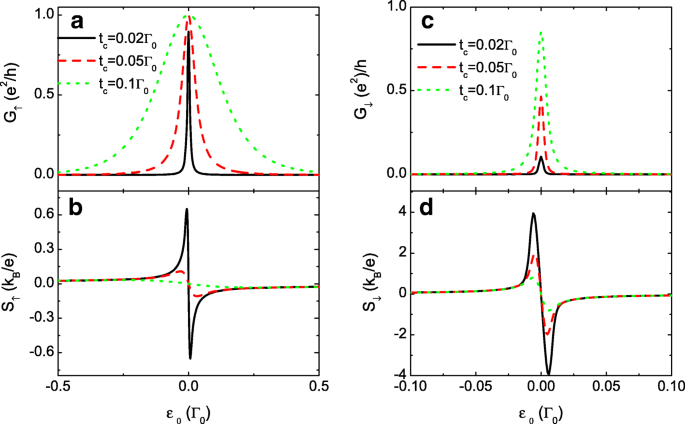
不同t的电导和热电势 c .自旋极化电导G σ 在 a 和 c , 和热电势 S σ 在 b 和 d 作为点级别 ε 的函数 p 为 0 =0.7 和 t 的不同值 c .其他参数如图2

如果 QD 以环形连接，则产生的 Fano 效应将极大地改变电导 [46] 和热电势的特性。特别是，巨大的热电偶出现在 Fano 反共振态附近，其中传输函数接近零 T σ (ε )=0 由于完全反射 [25-33]。替换电子能量ε 由化学势 μ 在方程式中(5)、可以找到唯一的反共振态位于

这仅由点间耦合决定，与其他参数无关，例如点水平 ε 1、ε 2、温度T 或点导混合矩阵 Γ α .因此，在如此复杂的系统中调节电导和热电量是相当简单的。 μ条件下 =0，反共振态只位于正ε 0 边。图 5a 和 b 显示了电导中的 Fano 反共振谷。图 5a 中的插图显示了大点级区域中电导的 Fano 线形状。与 t 的情况不同 0=0 其中热电势的零点位于ε 0=0，t 0≠0 处于反谐振状态，热电势与之反对称。对于 p 的情况 =0，两个自旋分量的热电势为零点在ε 0 =0.09，如图 5c 和 d 所示。随着 p 的增加 ，它们分开并移动到 0.09 的相反方向。在零点的两侧分别出现一个具有正负值的宽峰。值得一提的是，在其他点级区域中，热电势的值可以忽略不计，如图 5c 的插图所示。零点的移动以及热电势的峰值带来了两个有趣的结果。一个是 100 % 当 S 的峰值出现时，自旋极化热电势 ↑ 和 S ↓ 在能量空间中被相当大的 p 完全分开 价值。例如，参见图 5c 和 d 中的蓝色点划线 p =0.4。 ε的右侧 0=0.09，S的值 ↓ 接近于零但 S ↑ 有两个尖峰。而在 ε 的左侧 0=0.09，自旋热电势S ↓ 有两个峰值几乎为零 S ↑ .

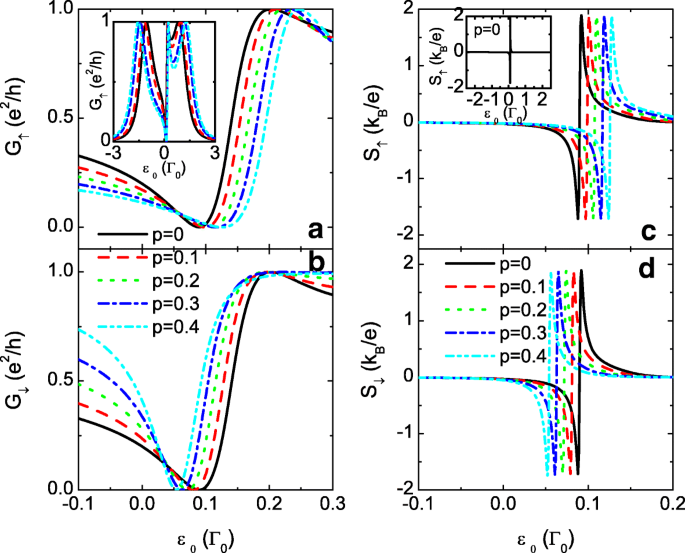
t 的电导和热电势 0=1。自旋极化电导G σ 在 a 和 b , 和热电势 S σ 在 c 和 d 作为点级别 ε 的函数 0 代表 t 0=1，t c =0.3 和不同点间耦合的自旋极化值p . a 中的插图 和 c 分别是大点水平范围内的电导和热电势。其他参数如图2

另一个有趣的结果是纯自旋热电势，即 S s =S ↑ -S ↓ ≠0 而 S e =S ↑ +S ↓ =0，或在有限热偏置下闭合电路中的纯自旋电流 [58]。这意味着大小相等的自旋向上和自旋向下的热电势符号相反。 S 的大小 s 当具有相反符号的自旋向下和自旋向上热电势的尖峰在相同的 ε 相遇时最大化 0 通过调整点间耦合的自旋极化 p .如图 6a 所示，S 中的零点和峰值 ↑ 和 S ↓ 分别向ε的左右移动 0=90k B T 由于 p ≠0。结果，自旋向上热电势的负峰值和自旋向下热电势中的正峰值同时出现在ε附近 0=90k B T 诱导纯自旋热电势。这通常发生在较小的 p 因为 S 中的两个窄峰 σ 非常接近零点，这由图 6a 中带有 p 的蓝色点划线证实 =0.02。为了清楚地显示小能量占优势，我们选择k B T 作为其中的能量单位。我们强调，这种纯自旋热电可以通过点间耦合的非常小的自旋极化获得，这可以通过在隧道势垒上施加弱磁场来实现。而且，纯自旋热电势的大小与电荷一（绿色虚线）一样大。

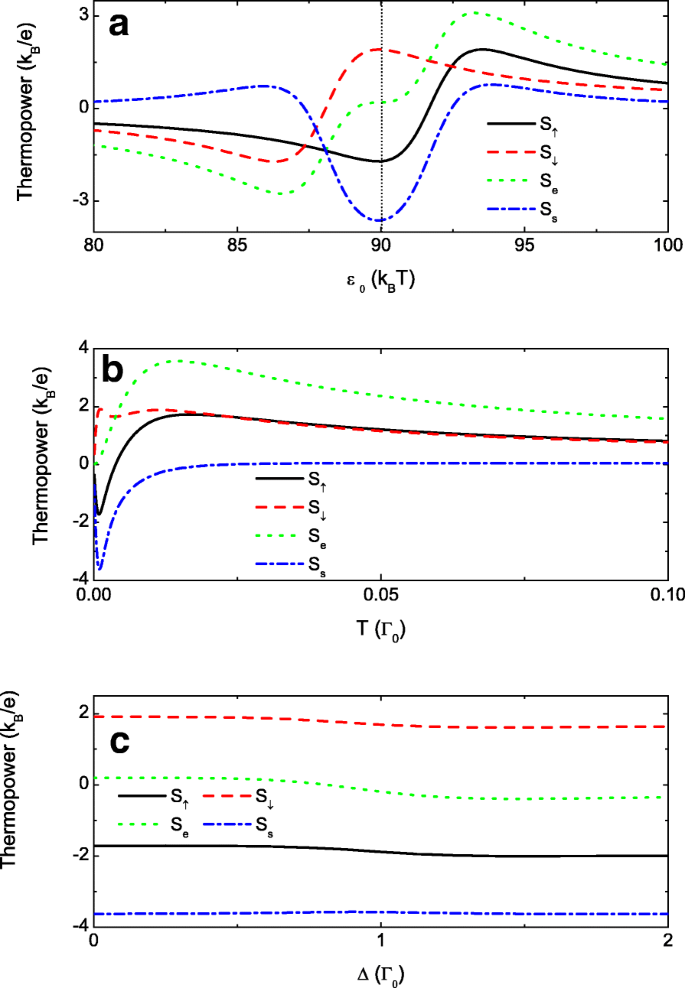
热电势的量子规律。 a中随点级变化的热电势 , b 中的温度 以及 c 中的电平失谐 .其他参数为 p =0.02，t 0=1，并且 t c =0.3。 b 中的点级别 和 c 被选为 ε 0=0.09Γ 0. 水平失谐Δ a 中的 =0 和 b , 温度为 T a 中的 =0.001 和 c

最后，我们展示了自旋分辨的纯自旋和随温度变化的电荷热电势T 和水平失谐Δ 分别在图 6b 和 d 中。点级ε 0 被选择为 0.09 以关注 Fano 反共振谷。图 6b 显示在低温下 S ↑ 和 S ↓ 发展出由实线和虚线表示的符号相反的峰，导致相当大的纯自旋热电S s （蓝色点划线）。现在充电热电S e 可以非常小，如绿色虚线所示。随着温度的升高，载流子的随机热运动破坏了 Fano 效应，S 中的峰值 σ 被涂抹。因此，S 之间的差异 ↑ 和 S ↓ 是无法区分的，纯自旋热电势趋于零。图 6d 显示纯自旋热电势对于点能级之间的差异 Δ 是稳健的 .这与方程的结果一致。 (7) Fano反共振态与点1和点2无关。

结论

总之，我们研究了串联或环形连接的 TQD 中的电导和热电特性，这些 TQD 与自旋相关的点间耦合。特别注意 100 % 的生成 自旋极化和纯自旋热电势。发现前者可以在具有足够大的点间耦合自旋极化的串行 TQD 配置中实现，当点彼此相当强耦合时。而如果点是弱耦合的，则巨大的 100 % 自旋极化热电可以在很小的点间耦合自旋极化下实现。当点呈圆形配置时，热电势相对于 Fano 反共振态是反对称的，热电势在该状态周围形成尖峰。通过改变点间耦合的自旋极化，自旋向上和自旋向下热电势的峰值在 QDs 能级范围内向相反的方向移动。现在 100 % 自旋极化和纯自旋热电势可以很容易地实现。目前的结果可以在点间耦合的自旋极化值较小的情况下获得，这在实验中是有利的。