什么是傅立叶变换？

本文为您提供有关数学技术的基本信息，该技术在系统设计和信号处理中起着绝对基础的作用。

以法国数学家约瑟夫·傅立叶命名，傅立叶变换是一种数学程序，可让我们确定频率内容 的一个函数。对于电气工程师，傅立叶变换通常应用于我们称为信号的时间函数 .

正如我们在示波器显示屏上看到的那样，电压或电流与时间的关系图是信号行为的直观表示。然而，这并不是唯一有用的表示。

在许多情况下，例如在 RF 系统的设计中，我们主要对信号的周期性行为感兴趣。更具体地说，我们有兴趣了解关于 sinusoidal 的信号周期性，因为正弦曲线是“纯”频率的唯一数学表达式。

傅里叶变换通过分解揭示信号的元素周期性将信号转换为其组成正弦频率并识别这些组成频率的幅度和相位。

“分解”一词在这里至关重要。傅里叶变换教导我们将时域信号视为由组成的波形不同幅度和相位的潜在正弦波形。

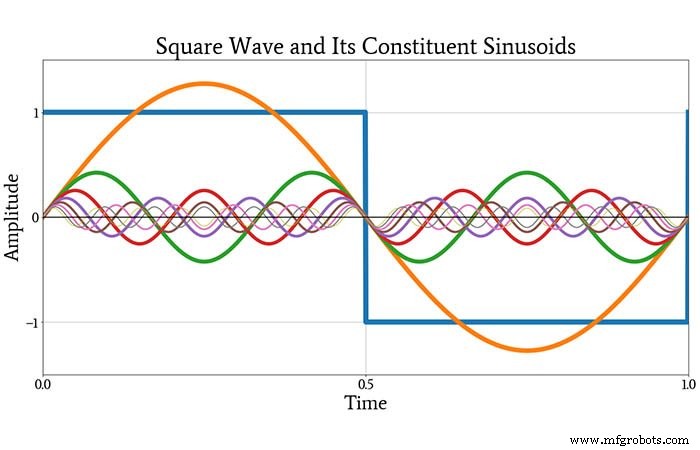
例如，方波可以分解为幅度稳定减小而频率稳定增加的无限系列正弦波。对于周期为 T、振幅为 A 的交流耦合方波，其精确级数可写为：

\[f_{square}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\ }}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]

我们可以把它转换成下面的形式，这样更直观一些：

\[f_{square}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3 }\sin(6\pi ft)+\frac{1}{5}\sin(10\pi ft)+\ ...\right)\]

其中 f 是方波的频率，单位为赫兹。

下图显示了原始方波（蓝色）和无限级数中的前八个正弦曲线。

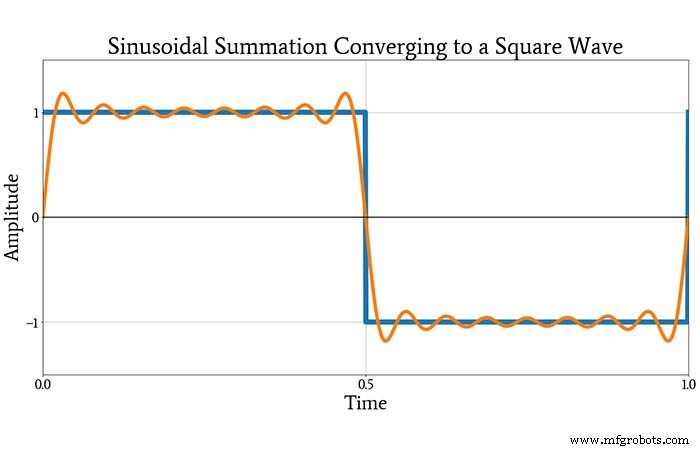
看过这个图后，你可能还是有点怀疑这些正弦曲线可以组合成方波。不过，下一个情节会让你信服。它显示了原始方波和相加产生的波形上面显示的所有组成正弦曲线。

当我们计算傅立叶变换时，我们从时间函数 f(t) 开始，然后通过数学分解，我们产生频率函数 F(ω)。（我们通常在傅立叶变换的理论讨论中使用角频率。）

在某个特定角频率（例如 100 rad/s）下评估 F(ω)，我们可以得到频率为 100 rad/s 的 f(t) 正弦分量的幅度和相位。如果 f(t) 在 100 rad/s 处没有正弦分量，则幅度为零。

您可能想知道函数 F(ω) 如何同时报告幅度和相位。傅里叶变换产生一个复数值 函数，这意味着变换本身既不是 f(t) 中频率分量的幅度，也不是这些分量的相位。与任何复数一样，我们必须执行额外的计算来提取幅度或相位。

当我们使用离散时，复值变换的概念更直观一些傅里叶变换，而不是“标准”变换，在这种变换中，我们以时间的符号函数开始，以频率的符号函数结束。

离散傅立叶变换对数值序列进行运算，并产生一系列傅立叶系数 .这些系数是典型的复数（即它们的形式为 a + jb），我们通常使用这些复数的大小，计算为 √(a² +b² )，在分析信号的频率成分时。

频率内容图在数据表、测试报告、教科书等中极为常见。我们经常将幅度与频率的关系图称为频谱——例如，“让我们看看信号的频谱”的意思是“让我们看看傅立叶变换中幅度信息的某种视觉表示.”

下图为幅值为1、频率为1Hz的交流耦合方波的频谱。

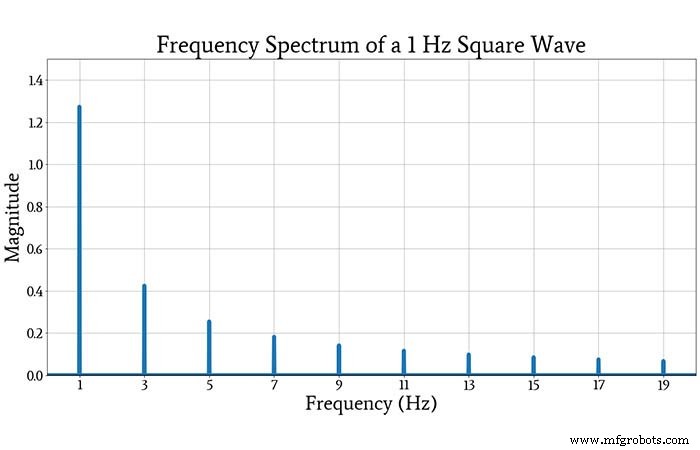
如果将绘制的频率“尖峰”幅度与上述无穷级数中相应正弦分量的幅度进行比较，您会发现它们是一致的。

这篇文章快结束了，我还没有告诉你我们实际上是如何生成数学定义的信号的傅立叶变换的。

老实说，我认为没有必要在介绍性文章中彻底探索数学细节：如今的频域分析主要由用户友好的、基于软件的技术主导，工程师不会花太多时间转换符号时间——域表达式转化为符号频域表达式。

尽管如此，对于像傅立叶变换这样重要的东西，至少了解基础数学是件好事。所以，不用多说，这就是我们如何将 f(t) 转换为 F(ω)：

\[F(\omega ) =\int\limits_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t} }dt}\]

我希望这篇文章对傅立叶变换是什么以及它如何让我们进一步了解信号的性质提供了一个清晰、直观的解释。

傅里叶变换只是一系列相关主题的开始；如果您想了解更多信息，请查看下面列出的文章。

云计算