线性化电阻传感器桥的两种技术

测量电阻传感器中微小的电阻变化可能是一项艰巨的任务。以下是消除桥接非线性误差的两种硬件方法。

电阻式传感器的电阻取决于物理变量，例如温度或力。这些器件的电阻变化百分比通常很小。例如，应变计电阻的总变化在其整个工作范围内可能小于 1%。

辨别这些小值需要高度精确的测量电路。桥接电路使我们能够更轻松地执行这些精确测量。然而，即使我们使用线性传感器，桥接电路的输出也可能与测量的物理变量存在非线性关系。

在这些情况下，我们可以使用软件或硬件技术来消除电桥非线性误差。在本文中，我们将介绍两种不同的电阻式传感器电桥线性化技术。

电阻式传感器的桥接非线性

考虑具有以下线性响应的电阻式压力传感器：

\[R_{sensor} =R_0 + Mx\]

其中 R0 是传感器在零压力下的初始电阻，x 是被测量（压力）的值，M 是传感器响应的斜率。为了使我们未来的方程更简单，我们假设 M 的值等于传感器的初始电阻值 (R0)，因此，传感器响应为 \[R_0(1+x)\]。

通常，电阻式传感器电阻的百分比变化很小，我们需要采用桥式电路来更轻松地进行精确测量。该传感器的常见桥配置如图 1 所示。

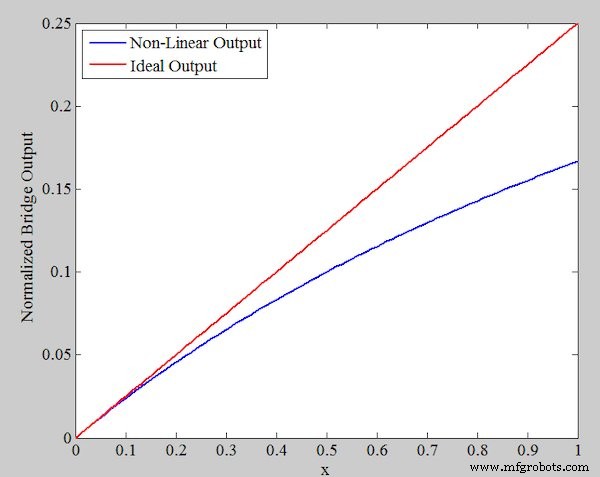
图 1。 电阻式传感器的常见电桥配置

注意电桥的其他三个电阻的阻值为R0。这种桥接电阻的选择可最大限度地提高输出 (Vout) 对传感器电阻变化的灵敏度。可以得到输出方程为：

\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\right)\]

这简化为：

\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]

等式 1.

如您所见，电桥输出与电阻值（x）的变化之间的关系不是线性的。使用\[x\ll2\]，我们可以通过以下线性关系来近似上述等式：

\[V_{out} \approx V_r\left(\frac{x}{4}\right)\]

等式 2。

图 2 描述了电桥的归一化输出 \[\frac{V_{out}}{V_r}\] 对于实际情况（等式 1）和理想输出（等式 2）。

图 2。 方程 1 和 2 的非线性（蓝色）和理想（红色）输出

正如预期的那样，与线性响应的偏差随 x 增加。

会引入多少非线性误差？

让我们量化上述桥接电路的非线性误差。我们可以将等式 1 改写为：

\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\right)\]

假设 \[\frac{x}{2} <<1\]，我们可以使用泰勒定理得到上述函数的近似值：

\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]

将此结果与等式 2 进行比较，我们可以计算出误差的大小为：

\[E_{Non-Linearity} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]

将其除以公式 2 给出的预期理想值，我们可以得到给定电阻 (x) 变化的百分比终点线性误差：

\[Percentage~Error =\frac{x}{2} \times 100\%\]

计算非线性误差的例子

考虑一个具有响应 \[R_{sensor} =R_0(1+x)\] 的传感器。假设 \[R_0 =100~\Omega\] 并且 x 在整个操作范围内的最大值为 0.01。最大线性误差百分比为：

\[Percentage~Error =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]

请注意，虽然我们可能能够使用软件来消除传感器线性误差，但线性响应是可取的，因为它可以提高测量精度并便于系统校准。有不同的电路拓扑结构可用于线性化桥式电路。

在本文的其余部分，我们将研究两种不同的桥接线性化技术。

方法 1：创建与电阻变化 (x) 成比例的电压

我们将在本文中讨论的第一种线性化技术如图 3 所示。让我们首先检查这种技术的基本思想，然后看看图 3 中的电路如何实现这一思想。

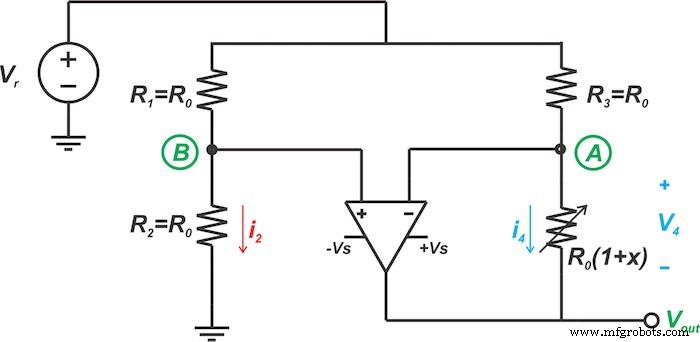
图 3。 一种电阻式传感器电桥线性化电路

图 4 显示了强制流过我们的线性传感器的固定电流 \[I_{Ref}\]。

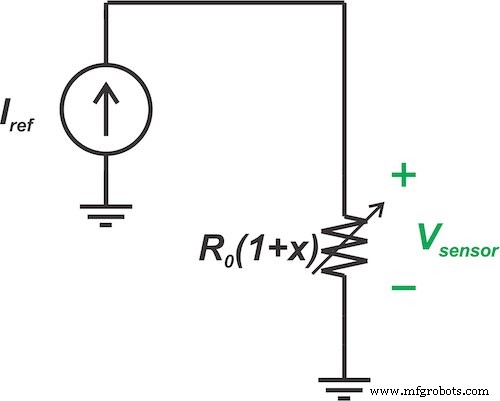
图 4。 强制通过线性传感器的固定电流 (IRef)

在这种情况下，传感器两端的最终电压为：

\[V_{sensor} =I_{Ref} \times R_0(1 + x)\]

可以重新排列为：

\[V_{sensor} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]

虽然第一项是常数值，但第二项与传感器电阻 (x) 的变化成正比。如果我们可以省略常数项，我们将得到一个与 x 呈线性关系的电压。

电路实现

图 3 中的电路使用上述思想对桥接电路进行线性化。由于运算放大器输入在理想情况下不吸收任何电流，因此节点 B 的电压将具有恒定值：

\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]

负反馈以及运算放大器的高增益将迫使运算放大器的反相和同相输入具有相同的电压：

\[v_A =v_B =\frac{V_r}{2}\]

由于 R3 的两端处于恒定电位，因此将有恒定电流流过。换句话说，运算放大器使 R3 充当电流源，迫使 \[\frac{V_r}{2R_0}\] 恒定电流进入传感器。因此，传感器两端的电压将为：

\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]

第一项是应该从 Vout 方程中消除的常数值。第二项与传感器电阻变化 (x) 成正比，应出现在输出方程中。应用基尔霍夫电压定律，我们发现 Vout 为：

\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]

因此，我们只需要 VA 等于 \[\frac{V_r}{2}\]。这已经满足了，这导致：

\[V_{out} =-\frac{V_r}{2}x\]

因此，输出与 x 呈线性关系。

方法 2：创建与阻力变化成比例的电流 (x)

我们将在本文中讨论的第二种桥接线性化技术如图 5 所示。

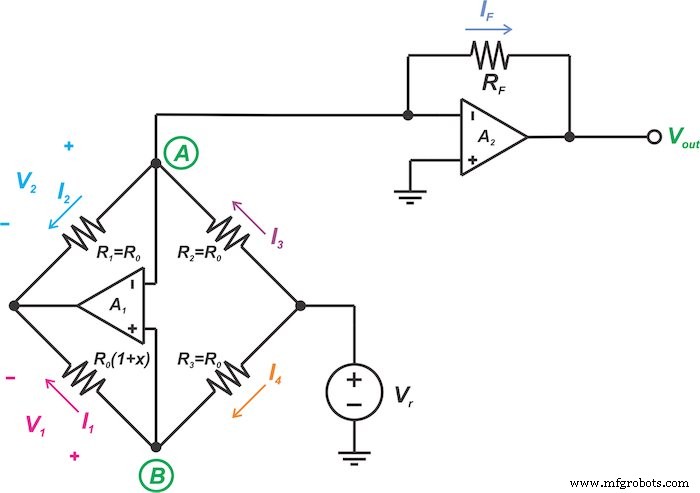
图 5。 另一种电阻式传感器电桥模拟线性化电路

让我们再次看一下该技术的基本思想，然后检查其电路实现。

第二种线性化技术如图 6 所示。

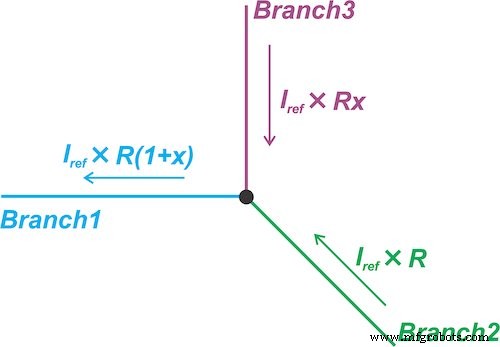
图 6。 线性化技术迫使通过电路分支的电流与传感器的电阻成正比

它强制通过电路分支（分支 1）的电流与传感器电阻成正比：

\[I_1 =I_{Ref} \times R_0(1 + x)\]

其中 IRef 是一个常数值。然后，它执行当前域减法以消除常数项\[I_{Ref} \times R_0\]。为此，通过分支 2 的电流设置为 \[I_{Ref} \times R_0\]。因此，通过分支 3 的电流将是 \[I_{Ref} \times R_0x\]— 与传感器电阻 (x) 的变化成正比。

电路实现

让我们看看图 5 中的电路如何实现上述想法。同样，负反馈以及运算放大器的高增益将迫使两个运算放大器（A1 和 A2）的反相和非反相输入具有相同的电压：

\[v_A =v_B =0\]

等式 3。

因此，我们有 V1 =V2 导致

\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]

这简化为：

\[I_2 =I_1 + I_1 \times x\]

等式 4。

我们知道 I1 =I4 并且，考虑到等式 3，我们有：

\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]

将其代入等式4，我们得到：

\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]

因此，I2 是一个常数值和一个与 x 成正比的项的总和。我们只需要利用基尔霍夫电流定律消除输出电流方程中的常数项即可。通过 R2 的电流产生的电流等于 \[\frac{V_r}{R_0}\] 到节点 A，导致：

\[I_F =-\frac{V_r}{R_0} \times x\]

因此，我们得到：

\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]

与第一种技术相比，图 5 中的电路需要一个额外的运算放大器。然而，对于这两种运放解决方案，我们可以通过选择\[\frac{R_F}{R_0}\] 比率来任意设置增益。

---

要查看我的文章的完整列表，请访问此页面。