量子物理学

“我认为可以肯定地说，没有人了解量子力学。” ——物理学家 Richard P. Feynman

说半导体器件的发明是一场革命，一点也不为过。这不仅是一项令人印象深刻的技术成就，而且为不可磨灭地改变现代社会的发展铺平了道路。半导体设备使微型电子产品成为可能，包括计算机、某些类型的医疗诊断和治疗设备以及流行的电信设备，仅举几例该技术的应用。

在这场技术革命的背后，是一场更伟大的普通科学革命：量子物理 .如果没有在理解自然世界方面的这种飞跃，半导体设备（以及仍在开发中的更先进的电子设备）的发展将永远不可能。量子物理学是一个极其复杂的科学领域。本章只是简要概述。当费曼这样的科学家说“没有人理解[它]”时，你可以肯定这是一个复杂的主题。但是，如果对量子物理学没有基本的了解，或者至少不了解导致其制定的科学发现，就不可能了解半导体电子设备的功能和原因。我读过的大多数入门电子教科书都试图从“经典”物理学的角度解释半导体，导致更多的混乱而不是理解。

原子

我们很多人都见过类似下图的原子图。

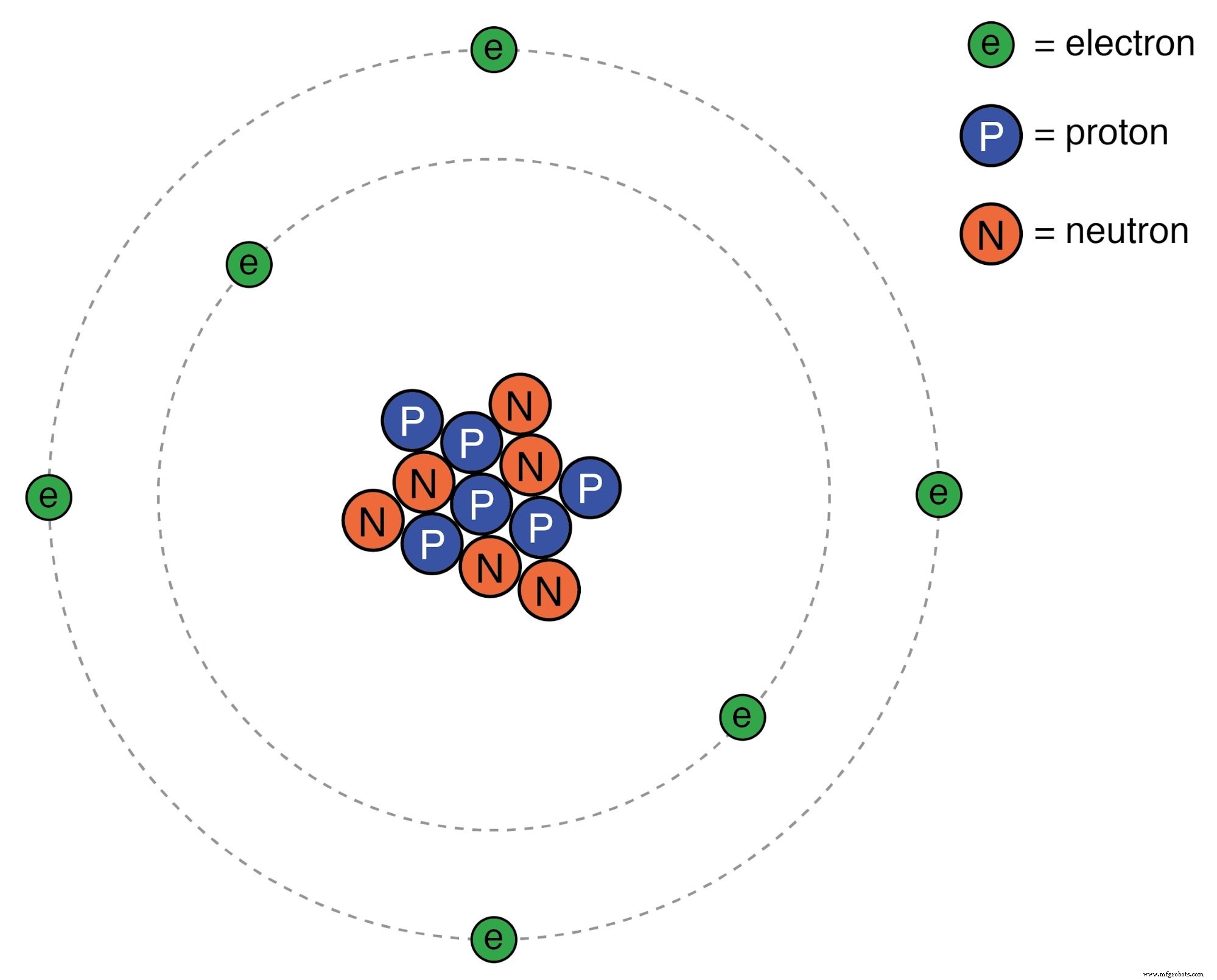
卢瑟福原子：负电子围绕一个小的正原子核运行。

称为质子的微小物质粒子 和中子 组成原子的中心； 电子 像行星一样围绕恒星运行。由于质子的存在（中子没有任何电荷），原子核带有正电荷，而原子的平衡负电荷则存在于轨道电子中。负电子被正质子吸引，就像行星被太阳引力吸引一样，但由于电子的运动，轨道是稳定的。我们将这种流行的原子模型归功于欧内斯特·卢瑟福 (Ernest Rutherford) 的工作，他在 1911 年左右通过实验确定原子的正电荷集中在一个微小而致密的核心中，而不是像早期研究人员提出的那样均匀分布在直径周围,JJ汤普森。

卢瑟福散射

卢瑟福的散射实验包括用带正电的 α 粒子轰击薄金箔，如下图所示。年轻的研究生 H. Geiger 和 E. Marsden 经历了意想不到的结果。一些 Alpha 粒子以大角度偏转。一些 Alpha 粒子被反向散射，以接近 180 ^o 的角度反弹 .大部分颗粒未偏转地穿过金箔，表明金箔大部分是空的。少数α粒子经历大偏转的事实表明存在一个极小的带正电的原子核。

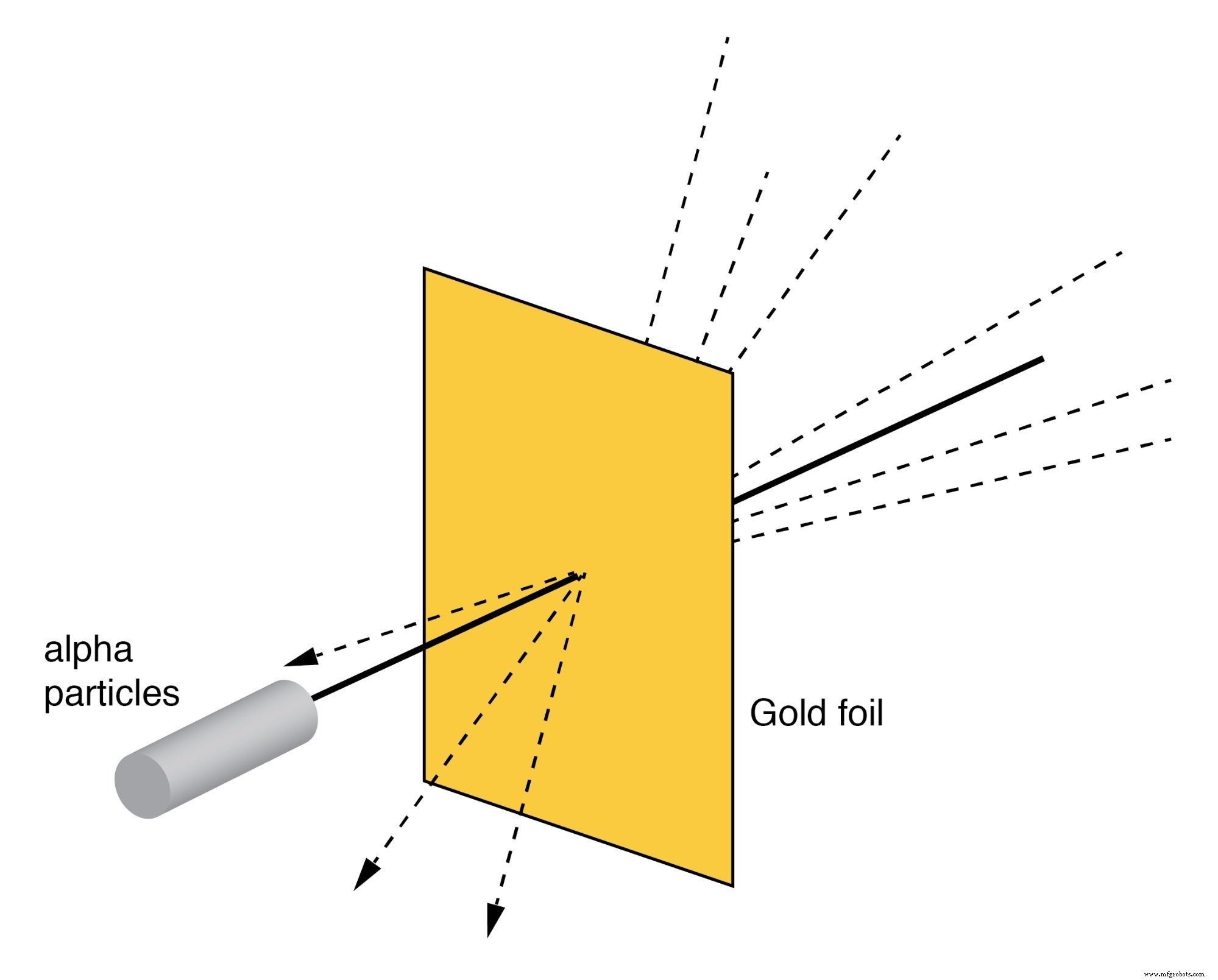
卢瑟福散射：一束α粒子被薄金箔散射。

尽管卢瑟福的原子模型比汤普森的原子模型更好地解释了实验数据，但它仍然不完美。进一步尝试定义原子结构，这些努力为量子物理学的奇异发现铺平了道路。今天我们对原子的理解要复杂得多。尽管如此，尽管量子物理学的革命及其对我们对原子结构的理解的贡献，卢瑟福的太阳系原子图像还是深深地嵌入了大众的意识中，以至于它在某些研究领域中仍然存在，即使在不合适的时候也是如此。

>

考虑一下摘自流行电子教科书的对原子中电子的简短描述：

轨道负电子因此被吸引到正原子核，这使我们产生了一个问题，即为什么电子不飞入原子核。答案是由于两个相等但相反的力，绕轨道运行的电子保持在它们的稳定轨道上。由于轨道而施加在电子上的离心向外力抵消了由于不同电荷而试图将电子拉向原子核的向内吸引力（向心）。

为了与卢瑟福模型保持一致，作者将电子投射为在圆形轨道上运行的固体物质块，它们对带相反电荷的原子核的向内吸引力通过它们的运动来平衡。提到“离心力”在技术上是不正确的（即使对于绕轨道运行的行星也是如此），但很容易被原谅，因为它被普遍接受：实际上，不存在推动任何的力这样的东西 轨道体离开 从它的轨道中心。似乎是这样，因为物体的惯性倾向于保持它沿直线运动，并且由于轨道与直线运动的偏差（加速度）是恒定的，因此对于将物体吸引到轨道的任何力都存在恒定的惯性阻力中心（向心），可以是重力、静电引力，甚至是机械连杆的张力。

然而，这种解释的真正问题在于电子首先在圆形轨道上运动的想法。加速电荷会发射电磁辐射是一个可证实的事实，这个事实甚至在卢瑟福的时代就已为人所知。由于轨道运动是加速度的一种形式（轨道物体以恒定加速度远离正常的直线运动），处于轨道状态的电子应该像旋转轮胎中的泥浆一样释放辐射。电子在称为同步加速器的粒子加速器中围绕圆形路径加速 已知这样做，结果称为同步辐射 .如果电子以这种方式失去能量，它们的轨道最终会衰减，导致与带正电的原子核发生碰撞。然而，这通常不会发生在原子中。事实上，电子“轨道”在各种条件下都非常稳定。

激发原子

此外，“受激”原子的实验表明，原子发射的电磁能仅在某些确定的频率下发生。众所周知，被光等外部影响“激发”的原子会吸收该能量并将其作为特定频率的电磁波返回，就像音叉无论如何敲击都会以固定的音调响起。当激发原子发出的光被棱镜分成其组成频率（颜色）时，光谱中会出现不同的颜色线，该光谱线的图案是该元素独有的。这种现象通常用于识别原子元素，甚至可以测量化合物或化学混合物中每种元素的比例。根据卢瑟福的太阳系原子模型（将电子视为以任何半径自由运行的物质块）和经典物理学定律，受激原子应该在几乎无限的频率范围内返回能量，而不是少数几个。换句话说，如果卢瑟福的模型是正确的，就不会有“音叉”效应，任何原子发出的光谱都会表现为一条连续的颜色带，而不是几条不同的线。

玻尔模型

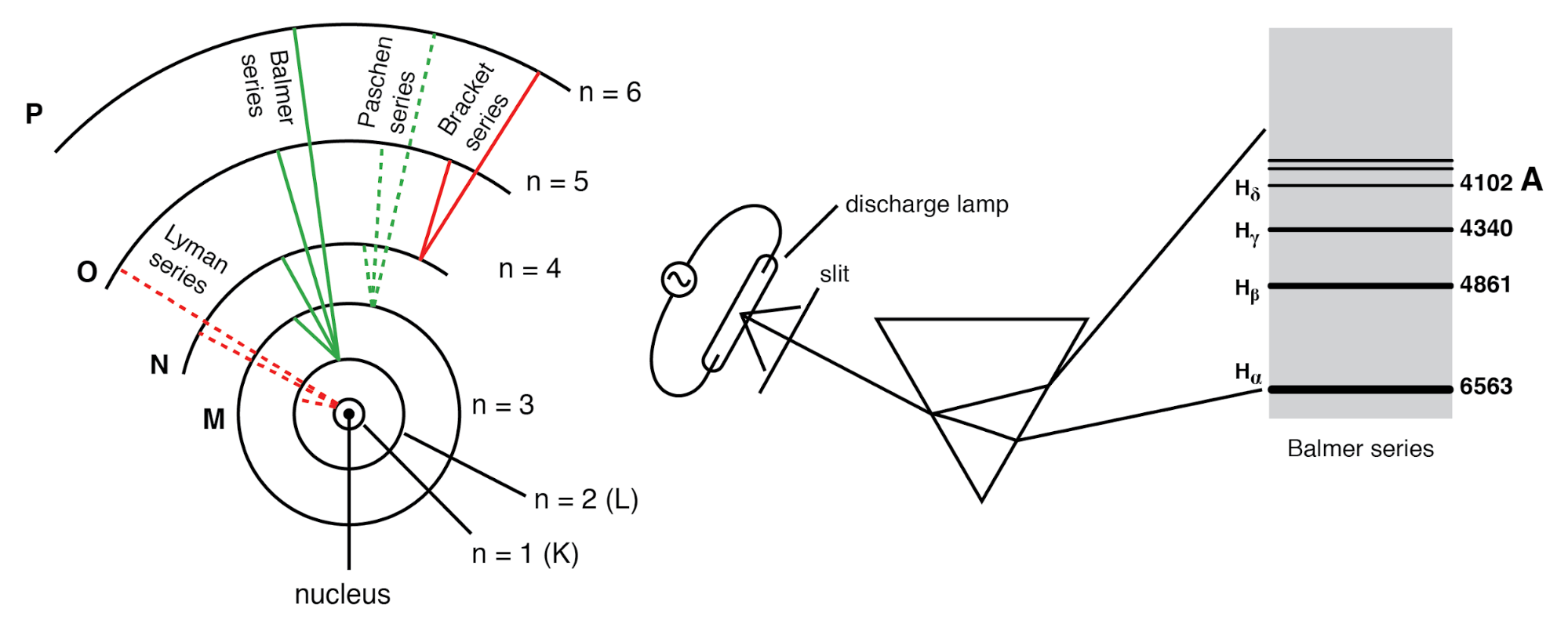
玻尔氢原子（轨道按比例绘制）只允许电子驻留在离散轨道中。从n=3、4、5或6下降到n=2的电子解释了Balmer谱线。

1912 年，一位名叫尼尔斯·玻尔的先驱研究人员在卢瑟福的实验室研究了几个月后，试图改进卢瑟福的模型。为了协调其他物理学家（最著名的是马克斯·普朗克和阿尔伯特·爱因斯坦）的发现，玻尔建议每个电子具有一定的特定能量，并且它们的轨道被量化 这样每个都可以占据原子核周围的某些位置，因为弹珠固定在原子核周围的圆形轨道上，而不是以前想象的自由移动的卫星。 （上图）根据电磁定律和加速电荷定律，玻尔将这些“轨道”称为静止状态 逃避他们在运动的暗示。尽管玻尔雄心勃勃地尝试以更接近实验结果的方式重新构建原子结构，这是物理学中的一个里程碑，但它还没有完成。他的数学分析比以前的模型分析对实验事件产生了更好的预测，但仍有一些关于为什么的悬而未决的问题 电子应该以如此奇怪的方式表现。电子存在于原子核周围的静止、量子化状态的断言比卢瑟福的模型更好地解释了实验数据，但他不知道什么会迫使电子表现出这些特定状态。大约十年后，这个问题的答案必须来自另一位物理学家路易斯·德布罗意。

德布罗意假设

德布罗意提出，电子作为光子（光的粒子）表现出粒子状和波状特性。在这个提议的基础上，他建议从波的角度而不是粒子的角度分析轨道电子可能更能理解它们的量子化性质。确实，在理解上又取得了突破。

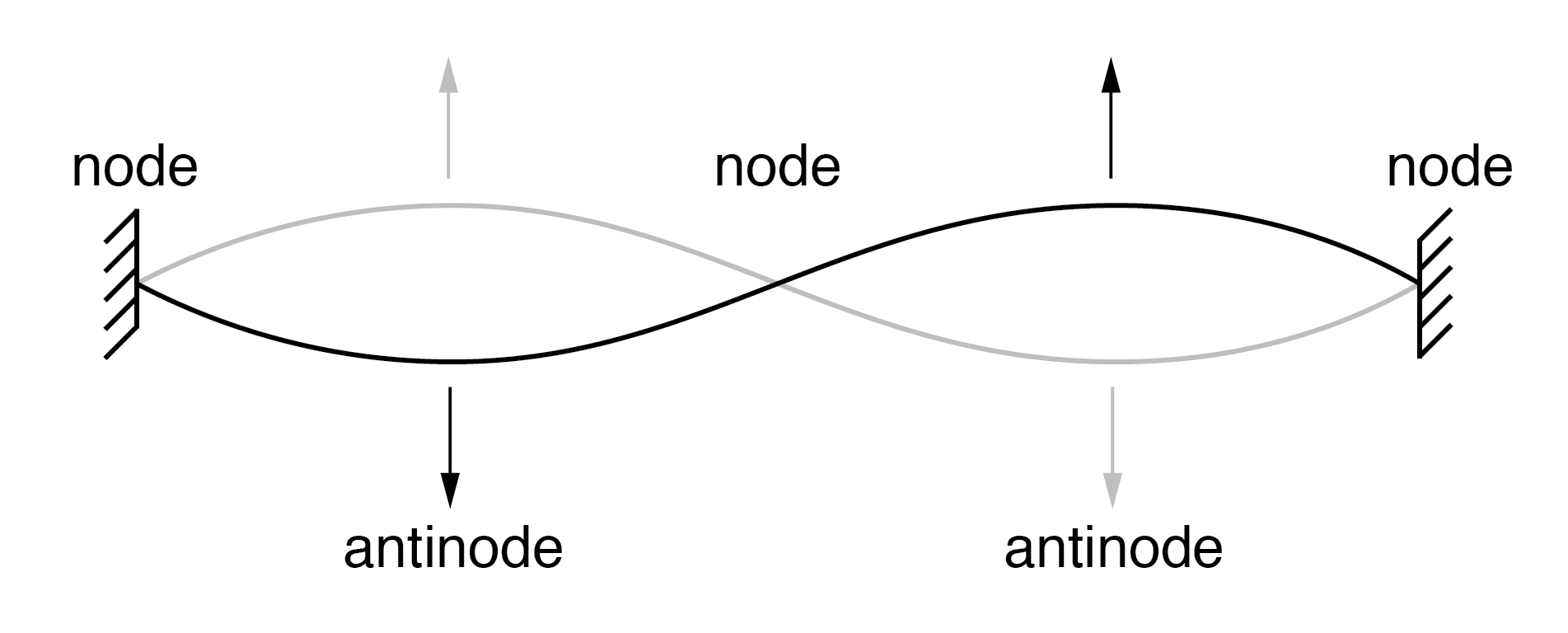
弦在两个固定点之间以共振频率振动形成驻波 .

根据德布罗意，原子由以驻波形式存在的电子组成 ，物理学家以各种形式众所周知的现象。正如乐器的弹拨弦（上图）以共振频率振动，“节点”和“波腹”沿其长度处于稳定位置。德布罗意设想原子周围的电子像波围绕一个圆圈弯曲一样站立，如下图所示。

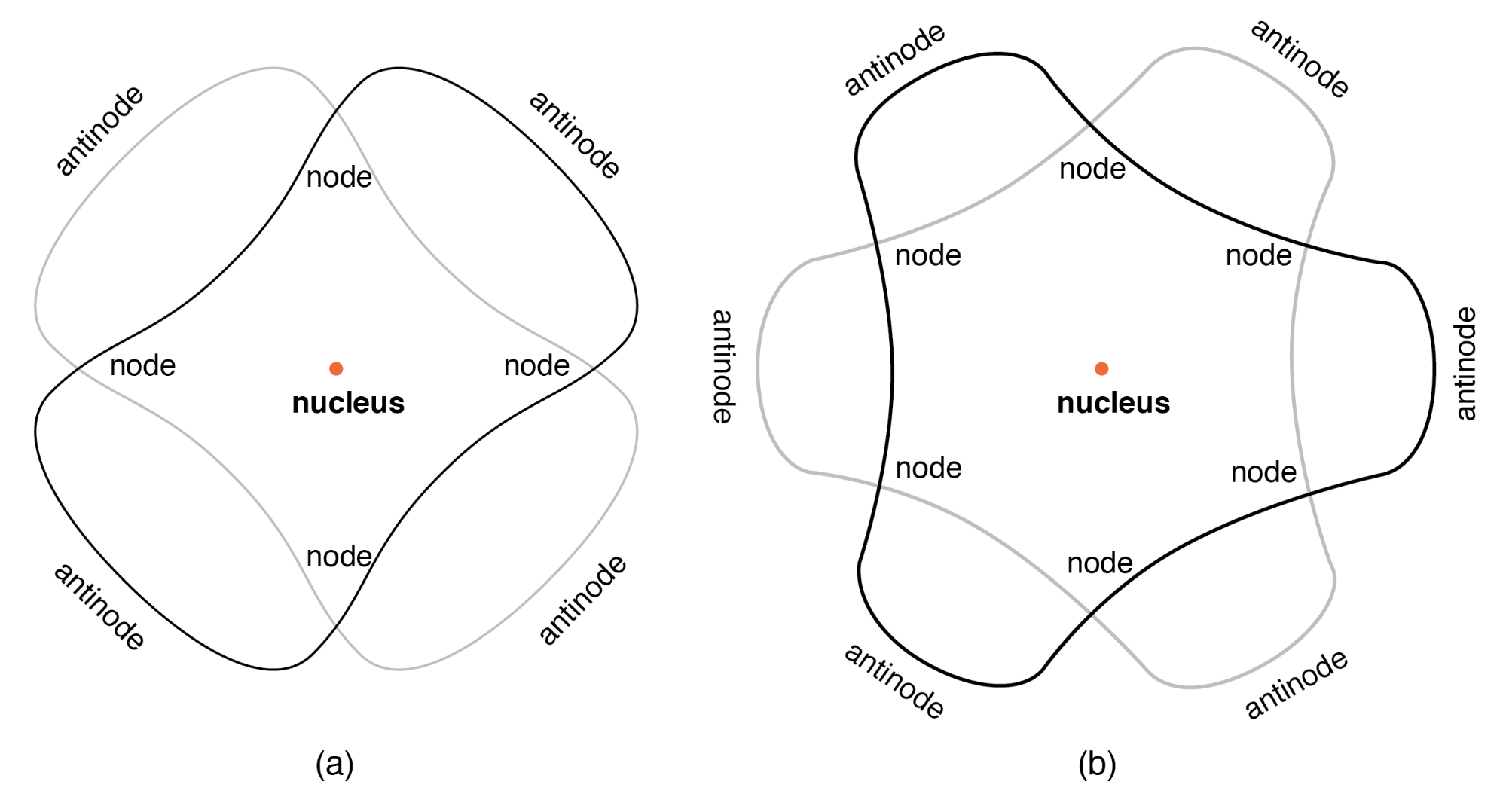
“轨道”电子作为驻波围绕原子核，(a) 每个轨道两个周期，(b) 每个轨道三个周期。

电子只能存在于特定的、确定的围绕原子核的“轨道”中，因为这是波末端唯一匹配的距离。在任何其他半径内，波应该与自身发生破坏性干涉，从而不复存在。德布罗意的假设既提供了数学支持，也提供了方便的物理类比来解释原子内电子的量子化状态，但他的原子模型仍然不完整。然而，在几年之内，物理学家维尔纳·海森堡和欧文·薛定谔，彼此独立工作，建立在德布罗意的物质波二元性概念的基础上，创建了在数学上更严格的亚原子粒子模型。

量子力学

这种从德布罗意原始驻波模型到海森堡矩阵和薛定谔微分方程模型的理论进步被命名为量子力学 ，它为亚原子粒子的世界引入了一个相当令人震惊的特征：概率或不确定性的特征。根据新的量子理论，不可能确定确切的位置和 一个粒子的精确动量。这个“不确定性原理”的流行解释是它是一个测量错误（即试图精确测量电子的位置，你会干扰它的动量，因此在进行位置测量之前无法知道它是什么，反之亦然）反之）。量子力学的惊人含义是粒子实际上没有精确的位置和 动量，而是以这样一种方式平衡这两个量，使它们的组合不确定性永远不会降低到某个最小值以下。

这种形式的“不确定性”关系存在于量子力学以外的领域。正如本系列丛书第二卷的“混频交流信号”一章所讨论的那样，波形的时域数据的确定性与其频域数据之间存在互斥关系。简单来说，我们越准确地知道它的组成频率，我们就越不准确地知道它的时间幅度，反之亦然。引用我自己的话：

可以绝对精确地分析无限持续时间（无限循环数）的波形，但计算机可用于分析的循环越少，分析的精确度就越低。 . .波循环的次数越少，其频率就越不确定。将这个概念推向其逻辑极端，短脉冲——一种甚至不能完成一个周期的波形——实际上没有频率，而是充当无限范围的频率。这一原理适用于所有基于波的现象，而不仅仅是交流电压和电流。

为了精确地确定变化信号的幅度，我们必须在非常窄的时间跨度内对其进行采样。然而，这样做限制了我们对波频率的看法。相反，为了非常精确地确定波的频率，我们必须在多个周期内对其进行采样，这意味着我们在任何给定时刻都无法看到其振幅。因此，我们无法以无限的精度同时知道任何波的瞬时幅度和总频率。更奇怪的是，这种不确定性不仅仅是观察者的不精确性。它存在于波浪的本质中。如果采用适当的技术，似乎不可能获得两者的精确测量值 瞬时幅度和频率同时进行。毫不夸张地说，波不可能同时具有精确的瞬时幅度和精确的频率。

海森堡和薛定谔所表达的粒子位置和动量的最小不确定性与测量限制无关；相反，它是粒子物质波二元性的内在属性。因此，电子实际上并不作为精确定义的物质位或精确定义的波形存在于它们的“轨道”中，而是作为“云”存在——技术术语是波函数 ——概率分布，就好像每个电子都在一系列位置和动量上“扩散”或“涂抹”。

这种将电子视为不精确云的激进观点起初似乎与量子化电子态的原始原理相矛盾：电子存在于原子核周围的离散、定义的“轨道”中。毕竟，正是这一发现导致了解释它的量子理论的形成。一个用来解释电子离散行为的理论最终宣布电子以“云”的形式存在，而不是作为离散的物质块存在，这看起来多么奇怪。然而，电子的量子化行为并不取决于具有确定位置和动量值的电子，而是取决于称为量子数的其他属性 .本质上，量子力学摒弃了普遍持有的绝对位置和绝对动量的概念，取而代之的是一种在共同经验中没有类似物的绝对概念。

四个量子数

尽管已知电子存在于空灵的“云状”分布概率形式而不是离散的物质块中，但这些“云”还有其他特征，是 离散的。原子中的任何电子都可以用四种数值度量来描述（前面提到的量子数 )，称为主体 , 角动量 , 磁性 , 和 旋转 数字。以下是这些数字含义的概要：

1.主量子数

主量子数： 用字母 n 表示 , 这个数字描述了 shell 电子驻留在其中。 电子“壳”是原子核周围允许电子存在的空间区域，对应于德布罗意和玻尔的稳定“驻波”模式。电子可以从壳层“跳跃”到壳层，但不能存在于之间 壳区。主量子数必须是正整数（整数，大于等于1）。换句话说，电子的原理量子数不能是 1/2 或 -3。这些整数值不是随意得出的，而是通过光谱的实验证据得出的：受激氢原子发出的光的不同频率（颜色）遵循数学上依赖于特定整数值的序列，如上图所示。

每个壳层都具有容纳多个电子的能力。电子壳的类比是圆形剧场的同心排座椅。就像坐在圆形剧场里的人必须选择一排坐（一个人不能坐在之间 排），电子必须“选择”一个特定的壳来“坐”。就像在圆形剧场的行中一样，最外层的壳比内壳容纳更多的电子。此外，电子往往会寻找最低的可用外壳，因为圆形剧场中的人们会寻找离中央舞台最近的座位。壳数越高，其中的电子能量越大。

任何壳层可以容纳的最大电子数由等式 2n ² 描述 ，其中“n”是主量子数。因此，第一个壳层 (n=1) 可以容纳 2 个电子；第二层 (n=2) 8 个电子，第三层 (n=3) 18 个电子。 （下图）

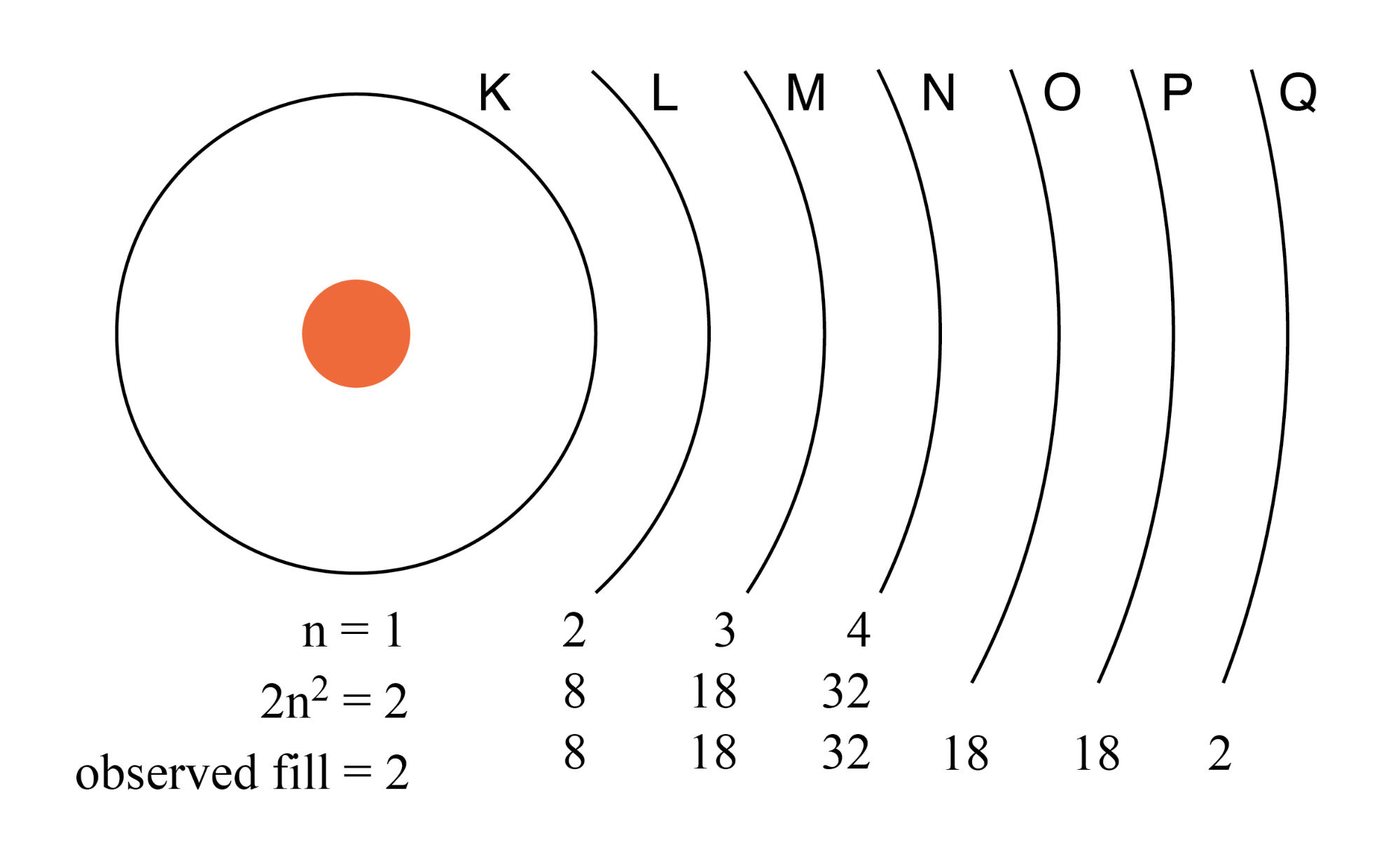
原子中的电子壳以前用字母而不是数字来表示。第一个壳（n=1）标记为K，第二个壳（n=2）L，第三个壳（n=3）M，第四个壳（n=4）N，第五个壳（n=5） O，第六层（n=6）P，第七层（n=7）Q。

2.角动量量子数

角动量量子数： 一个壳，由子壳组成。人们可能倾向于将子壳视为壳的简单细分，如分隔道路的车道。子壳要奇怪得多。子壳是允许存在电子“云”的空间区域，不同的子壳实际上具有不同的形状。第一个子壳的形状像一个球体（下图），当将其可视化为围绕原子核的三维电子云时，这是有道理的。然而，第二个子壳类似于一个哑铃，由在原子中心附近的一个点连接在一起的两个“叶”组成。 （下图（p））第三个子壳通常类似于围绕原子核聚集的一组四个“裂片”。这些子壳形状让人想起无线电天线信号强度的图形描述，球状叶状区域从天线向各个方向延伸。 （下图（d））

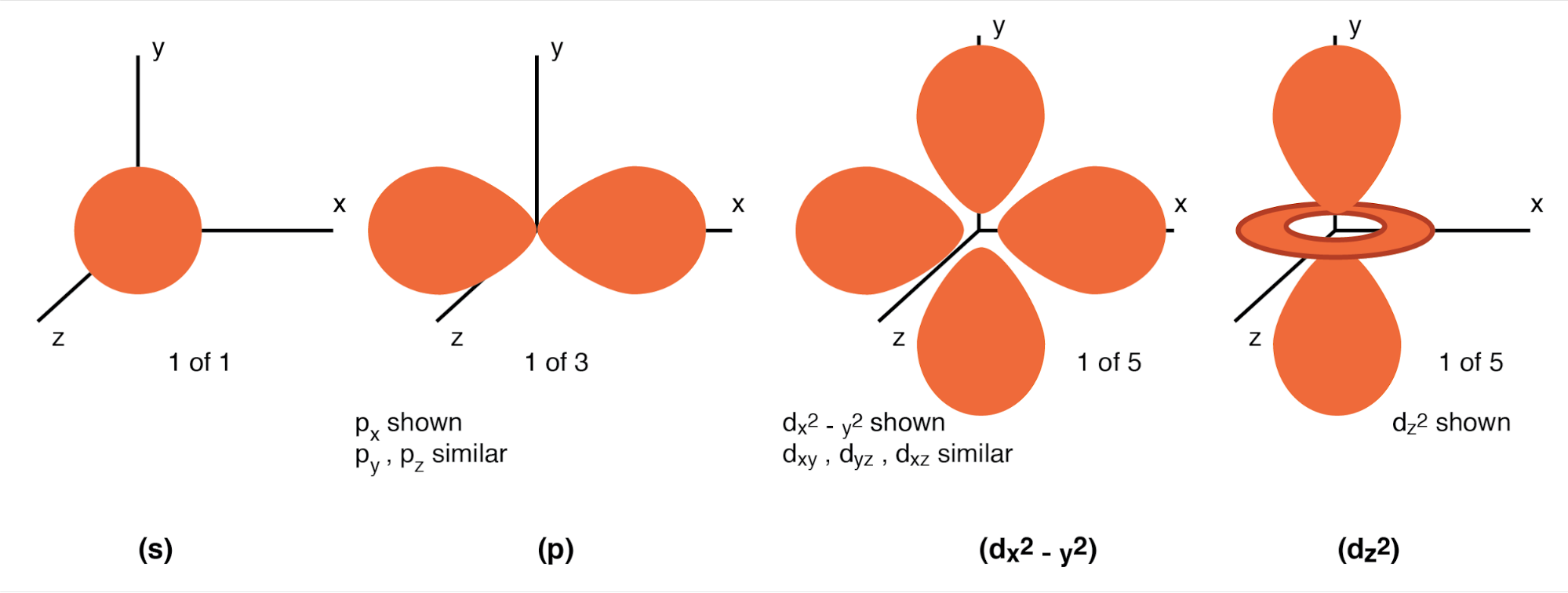
有效的角动量量子数是正整数，如主量子数，但也包括零。这些电子的量子数用字母 l 表示。壳中子壳的数量等于壳的主量子数。因此，第一个壳 (n=1) 有一个子壳，编号为 0；第二个外壳（n=2）有两个子外壳，编号为 0 和 1；第三个壳（n=3）有三个子壳，编号为0、1和2。

子外壳描述的旧约定使用字母而不是数字。在该符号中，第一个子壳 (l=0) 指定为 s，第二个子壳 (l=1) 指定为 p，第三个子壳 (l=2) 指定为 d，第四个子壳 (l=3) 指定为 f。这些字母来自sharp、principal（不要与主量子数n混淆）、diffuse和basic。您仍然会在许多元素周期表中看到这种符号约定，用于指定原子最外层或价壳的电子配置。 （下图）

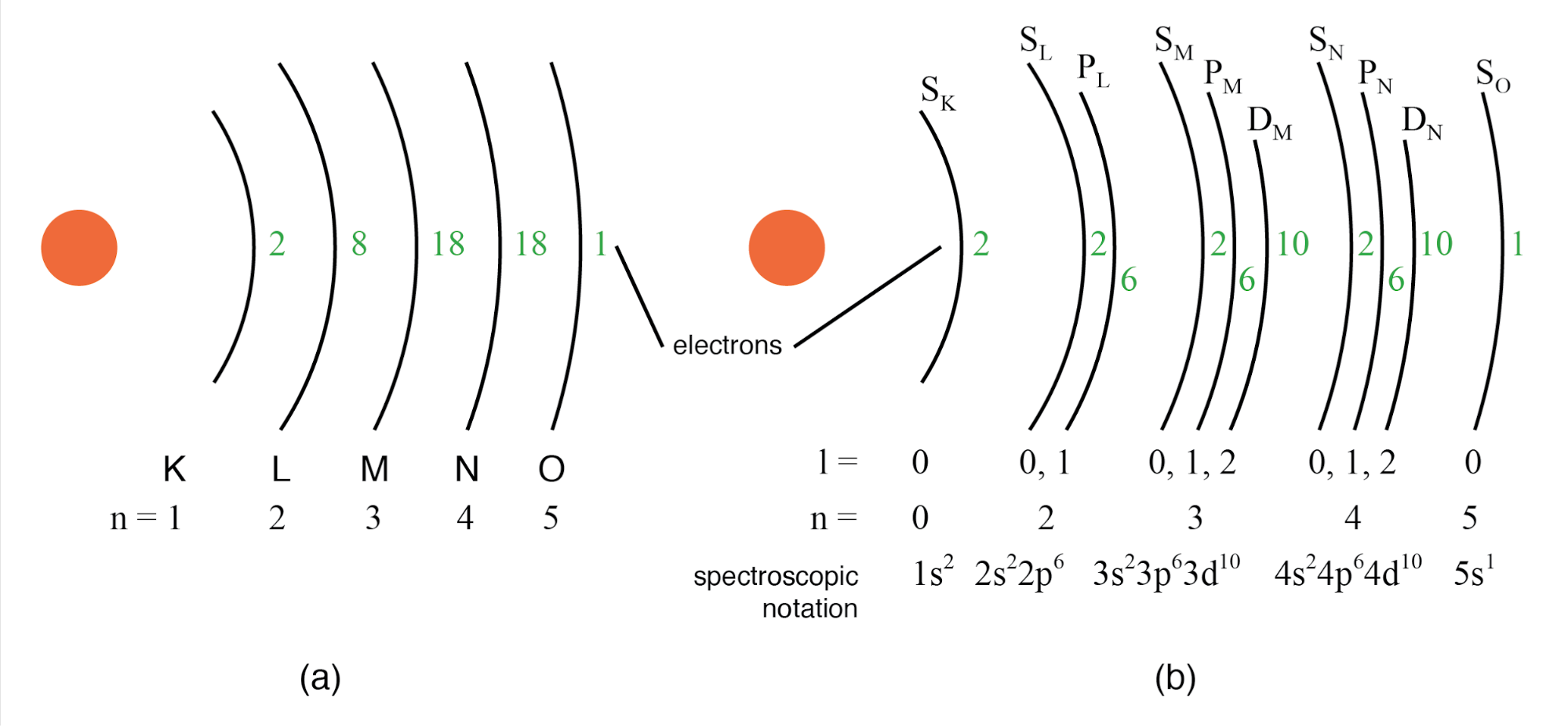
(a) 银原子的玻尔表示，(b) Ag 的子壳表示，将壳分成子壳（角量子数 l）。该图并未暗示电子的实际位置，但代表了能级。

3.磁量子数

磁性量子数： 电子的磁量子数分类其子壳形状指向的方向。子壳的“波瓣”指向多个方向。这些不同的方向被称为轨道 .对于第一个子壳 (s; l=0)，它类似于一个没有“方向”的球体，因此只有一个轨道。对于每个壳中的第二个 (p; l=1) 子壳，它类似于指向三个可能方向的哑铃。想象三个哑铃在原点相交，每个哑铃在三轴坐标空间中沿不同的轴定向。

此量子数的有效数值由范围从 -l 到 l 的整数组成，并被符号化为 m 我 在原子物理学和l z 在核物理学中。要计算任何给定子壳中的轨道数，请将子壳数加倍并加 1，(2·l + 1)。例如，任何壳层中的第一个子壳层 (l=0) 包含一个轨道，编号为 0；任何壳中的第二个子壳 (l=1) 包含三个轨道，编号为 -1、0 和 1；第三个子壳层 (l=2) 包含五个轨道，编号为 -2、-1、0、1 和 2；等等。

与主量子数一样，磁量子数直接来自实验证据：塞曼效应，通过将电离气体暴露在磁场中来划分谱线，因此得名“磁”量子数。

4.自旋量子数

自旋量子数： 与磁量子数一样，原子电子的这种特性也是通过实验发现的。仔细观察谱线发现每条谱线实际上是一对间隔非常近的谱线，这种所谓的精细结构 假设是由于每个电子像行星一样在轴上“旋转”。具有不同“自旋”的电子在激发时会发出略有不同的光频率。名称“自旋”被分配给这个量子数。旋转电子的概念现在已经过时，更适合将电子视为离散的物质块而不是“云”的（错误）观点；但是，名字还在。

自旋量子数用 m 表示 s 在原子物理学和s z 在核物理学中。对于每个壳层的每个子壳层中的每个轨道，可能有两个电子，一个自旋为+1/2，另一个自旋为-1/2。

泡利排除原则

物理学家沃尔夫冈·泡利 (Wolfgang Pauli) 开发了一个原理，可以根据这些量子数来解释原子中电子的排序。他的原理称为泡利不相容原理 , 指出在同一个原子中没有两个电子可以占据完全相同的量子态。也就是说，原子中的每个电子都有一组唯一的量子数。这限制了可能占据任何给定轨道、亚壳层和壳层的电子数量。

此处显示的是氢原子的电子排列：

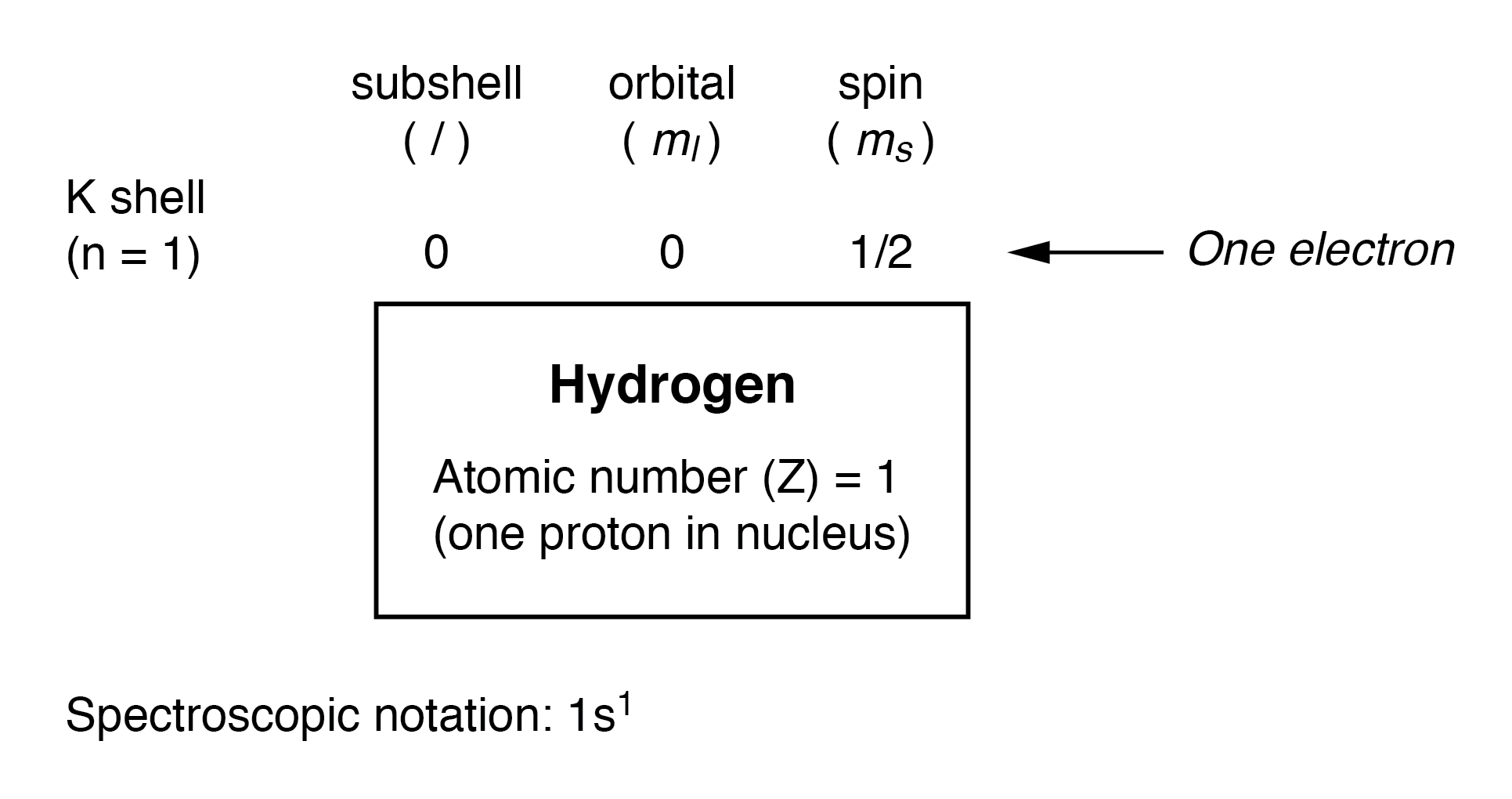
原子核中有一个质子，需要一个电子来静电平衡原子（质子的正电荷与电子的负电荷完全平衡）。这个电子位于最低层 (n=1)，第一个子层 (l=0)，位于该子层 (ml=0) 的唯一轨道（空间方向）中，自旋值为 1/2。描述这种组织的一种常用方法是在称为光谱符号的约定中根据电子的壳层和子壳层列出电子 .在这种表示法中，壳数显示为整数，子壳显示为字母 (s,p,d,f)，子壳中的电子总数（所有轨道，所有自旋）作为上标。因此，氢，其孤电子位于基能级，被描述为 1s ¹ .

继续下一个原子（按原子序数），我们有元素氦：

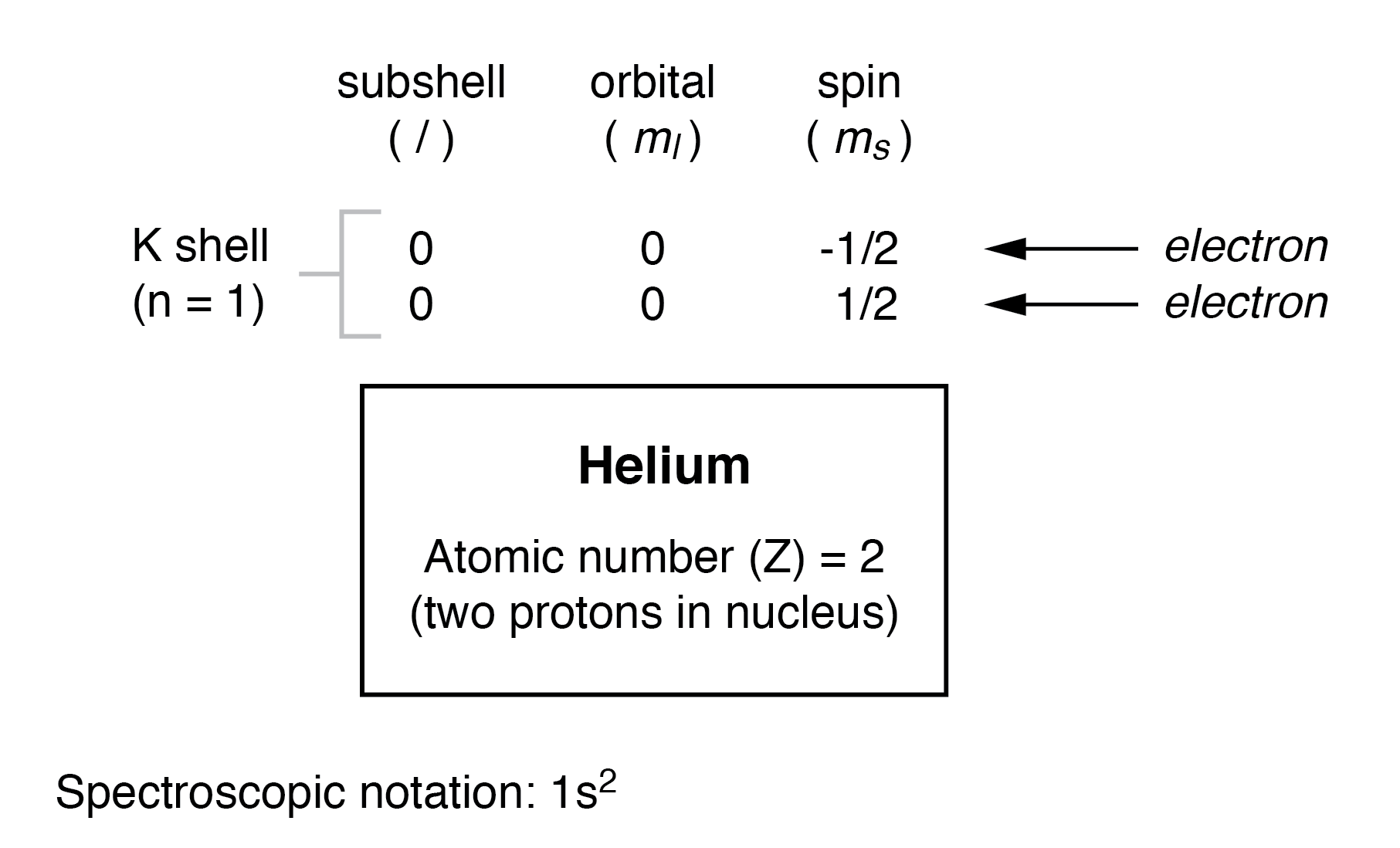
氦原子的原子核中有两个质子，这需要两个电子来平衡双正电荷。由于两个电子——一个自旋=1/2，另一个自旋=-1/2——适合一个轨道，氦的电子配置不需要额外的子壳或壳来容纳第二个电子。

但是，需要三个或更多电子的原子将 需要额外的子壳来容纳所有电子，因为只有两个电子适合最低壳 (n=1)。考虑原子序数递增序列中的下一个原子，锂：

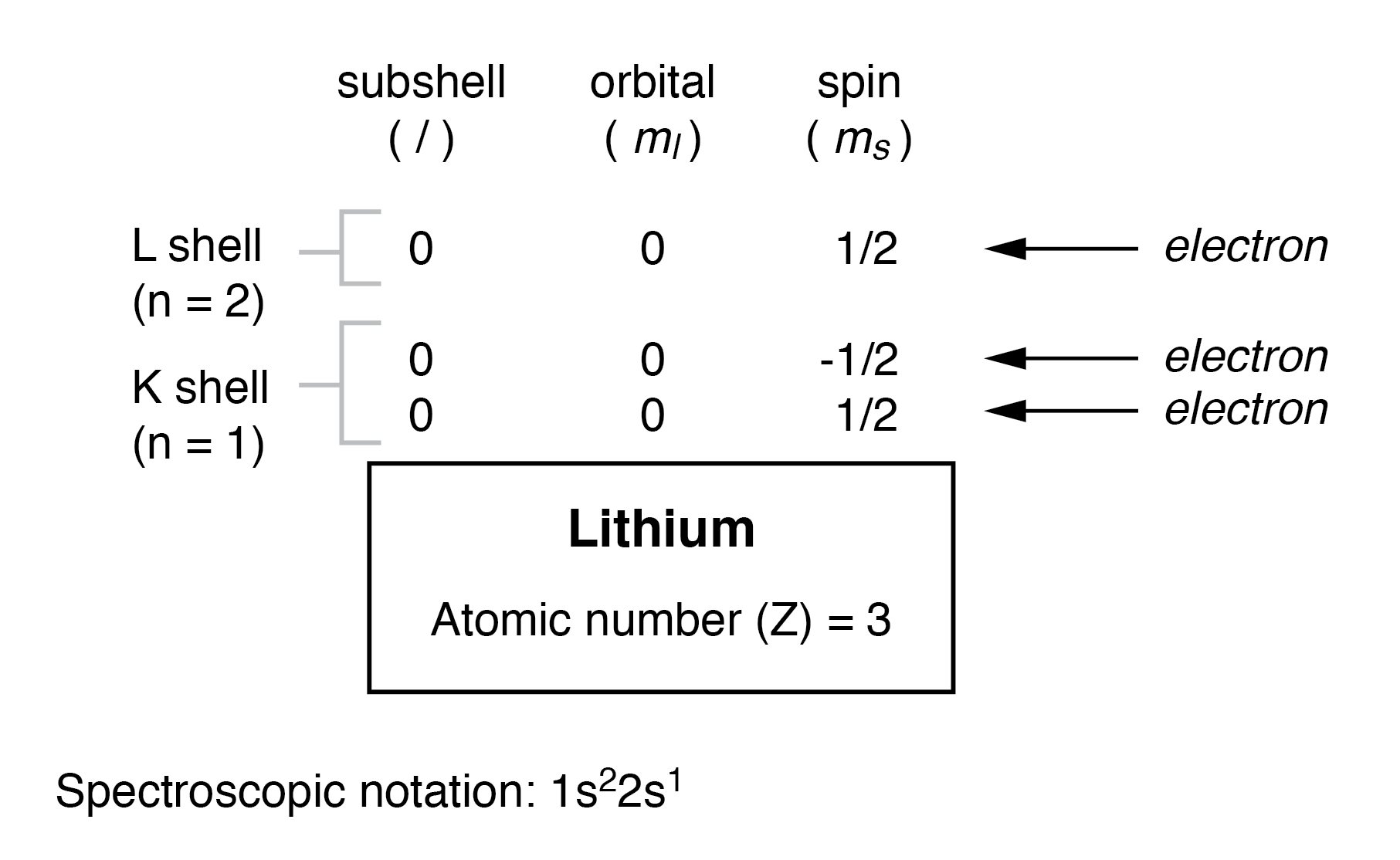
锂原子使用 L 壳 (n=2) 容量的一小部分。这个壳实际上有八个电子的总容量（最大壳容量 =2n ² 电子）。如果我们检查具有完全填充的 L 壳层的原子的组织，我们将看到子壳层、轨道和自旋的所有组合如何被电子占据：

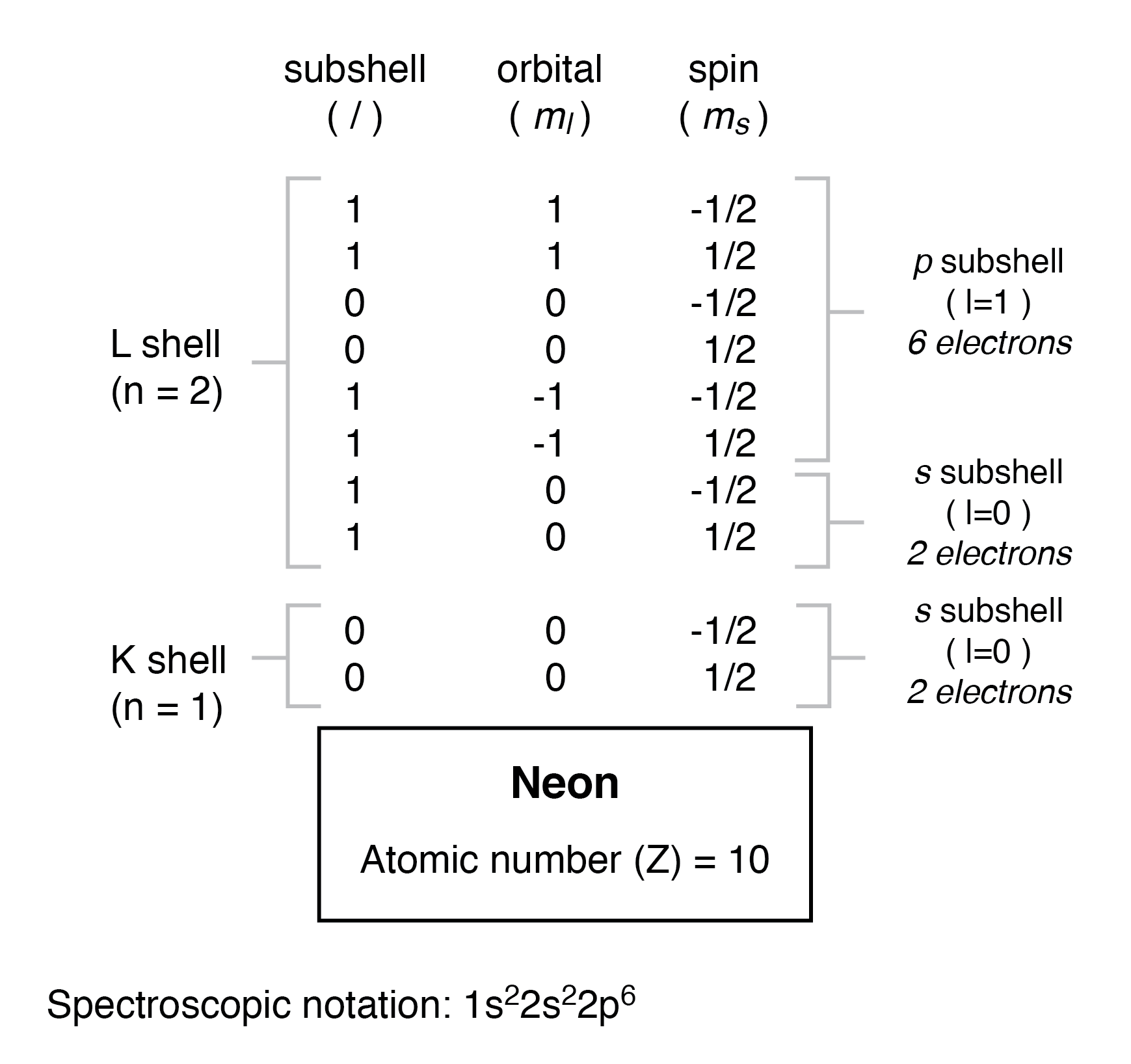
通常，当为原子给出光谱符号时，任何完全填充的壳都被省略，未填充或最高级别填充的壳被表示。例如，具有两个完全填充壳的氖元素（如上图所示）在光谱上可以简单地描述为 2p ⁶ 而不是 1s ² 2s ² 2p ⁶ .锂，其 K 壳层完全充满，L 壳层中有一个孤立电子，可以简单地描述为 2s ¹ 而不是 1s ² 2s ¹ .

完全填充的低层壳的省略不仅仅是符号上的方便。它还说明了化学的基本原理：元素的化学行为主要由其未填充的壳决定。氢和锂的最外层都只有一个电子 (1s ¹ 和 2s ¹ ，分别），赋予这两个元素一些相似的属性。两者都是高度反应性的，并且以几乎相同的方式反应（以相似的模式与相似的元素结合）。锂在其几乎空置的 L 壳下面有一个完全填充的 K 壳无关紧要：未填充的 L 壳是决定其化学行为的壳。

具有完全填充外壳的元素被归类为高贵 ，并以与其他元素几乎完全不反应为特征。这些元素过去被归类为 inert ，当时人们认为这些是完全不反应的，但现在已知在特定条件下会与其他元素形成化合物。

周期表

由于在最外层具有相同电子构型的元素表现出相似的化学性质，因此德米特里·门捷列夫将不同的元素相应地组织在一张表中。这样的表被称为元素周期表 ，现代表格遵循下图中的这种一般形式。

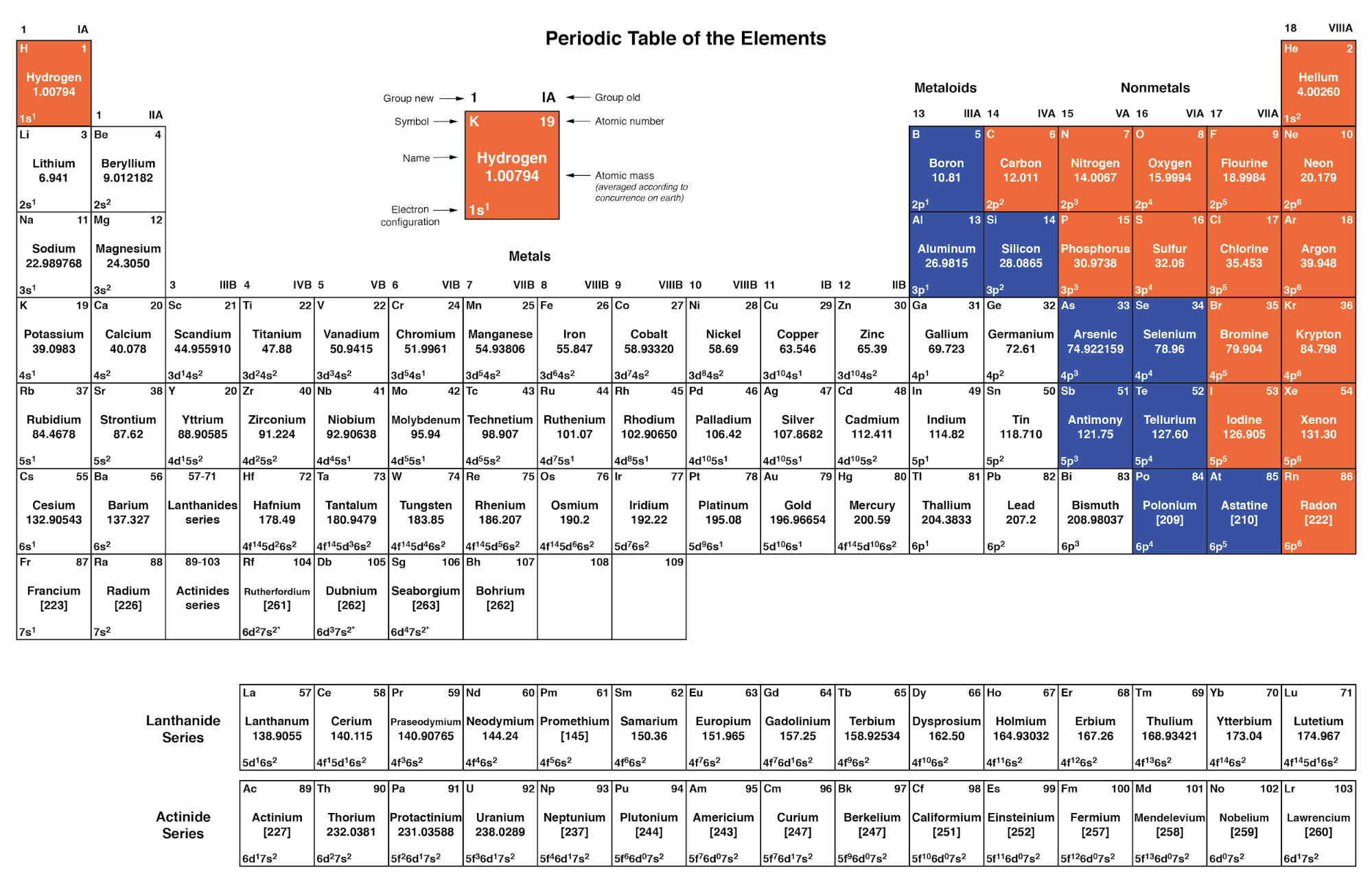
化学元素周期表

俄罗斯化学家德米特里·门捷列夫是第一个制定元素周期表的人。尽管门捷列夫根据原子质量而不是原子序数来组织他的表格，并且制作的表格不如现代元素周期表有用，但他的发展是科学证明的一个很好的例子。看到周期性模式（根据原子质量的类似化学性质），门捷列夫假设所有元素都应该符合这个有序方案。当他发现表格中的“空白”点时，他遵循现有秩序的逻辑，假设存在迄今为止未被发现的元素。随后这些元素的发现为门捷列夫的假设提供了科学依据，进一步推动了未来的发现，并形成了我们今天使用的元素周期表。

这就是科学应该 工作：假设遵循其逻辑结论，并根据实验数据与这些结论的一致性所确定的接受、修改或拒绝。任何傻瓜都可能在事后制定假设来解释现有的实验数据，许多人确实如此。什么使科学假设与事后区分开来 推测是对尚未收集的未来实验数据的预测，以及由于该数据而反驳的可能性。大胆地遵循假设得出其合乎逻辑的结论并敢于预测未来实验的结果并不是信仰的教条飞跃，而是对该假设的公开测试，任何能够产生矛盾数据的人都可以对其进行挑战。换句话说，由于声称可以预测尚未进行的实验的结果，科学假设总是“有风险的”，因此如果实验结果不如预期，则容易被反驳。 Thus, if a hypothesis successfully predicts the results of repeated experiments, its falsehood is disproven.

Quantum Mechanics From Hypothesis to Theory

Quantum mechanics, first as a hypothesis and later as a theory, has proven to be extremely successful in predicting experimental results, hence the high degree of scientific confidence placed in it. Many scientists have reason to believe that it is an incomplete theory, though, as its predictions hold true more at micro physical scales than at macro scopic dimensions, but nevertheless it is a tremendously useful theory in explaining and predicting the interactions of particles and atoms.

As you have already seen in this chapter, quantum physics is essential in describing and predicting many different phenomena. In the next section, we will see its significance in the electrical conductivity of solid substances, including semiconductors. Simply put, nothing in chemistry or solid-state physics makes sense within the popular theoretical framework of electrons existing as discrete chunks of matter, whirling around atomic nuclei like miniature satellites. It is when electrons are viewed as “wave functions” existing in definite, discrete states that the regular and periodic behavior of matter can be explained.

评论：

• Electrons in atoms exist in “clouds” of distributed probability, not as discrete chunks of matter orbiting the nucleus like tiny satellites, as common illustrations of atoms show.
• Individual electrons around an atomic nucleus seek unique “states,” described by four quantum numbers :the Principal Quantum Number , known as the shell; the Angular Momentum Quantum Number , known as the subshell; the Magnetic Quantum Number , describing the orbital (subshell orientation); and the Spin Quantum Number , or simply spin . These states are quantized, meaning that no “in-between” conditions exist for an electron other than those states that fit into the quantum numbering scheme.
• The Principal Quantum Number (n ) describes the basic level or shell that an electron resides in. The larger this number, the greater radius the electron cloud has from the atom’s nucleus, and the greater that electron’s energy. Principal quantum numbers are whole numbers (positive integers).
• The Angular Momentum Quantum Number (l ) describes the shape of the electron cloud within a particular shell or level, and is often known as the “subshell.” There are as many subshells (electron cloud shapes) in any given shell as that shell’s principal quantum number. Angular momentum quantum numbers are positive integers beginning at zero and ending at one less than the principal quantum number (n-1).
• The Magnetic Quantum Number (m l ) describes which orientation a subshell (electron cloud shape) has. Subshells may assume as many different orientations as 2-times the subshell number (l ) plus 1, (2l+1) (E.g. for l=1, ml=-1, 0, 1) and each unique orientation is called an orbital . These numbers are integers ranging from the negative value of the subshell number (l ) through 0 to the positive value of the subshell number.
• The Spin Quantum Number (m s ) describes another property of an electron, and may be a value of +1/2 or -1/2.
• Pauli’s Exclusion Principle says that no two electrons in an atom may share the exact same set of quantum numbers. Therefore, no more than two electrons may occupy each orbital (spin=1/2 and spin=-1/2), 2l+1 orbitals in every subshell, and n subshells in every shell, and no more.
• Spectroscopic notation is a convention for denoting the electron configuration of an atom. Shells are shown as whole numbers, followed by subshell letters (s,p,d,f), with superscripted numbers totaling the number of electrons residing in each respective subshell.
• An atom’s chemical behavior is solely determined by the electrons in the unfilled shells. Low-level shells that are completely filled have little or no effect on the chemical bonding characteristics of elements.
• Elements with completely filled electron shells are almost entirely unreactive, and are called noble (formerly known as inert ).

相关工作表：

• Atomic Structure Worksheet
• Basic Electricity Worksheet