使用互调多项式和有效位数对 ADC 建模

在本文中，我们将讨论如何在系统仿真中对 ADC 进行建模的另一种方法，这次是通过使用有效位数并调整我们的 ADC通过向理想量化器输入引入 5 阶多项式。

到目前为止，在本系列中，我们已经讨论了在系统仿真中对数据转换器进行建模的各种方法的优点，特别是使用使用有效位数或 ENOB 的建模方法。

现在，我们将通过添加一个新元素来继续讨论：使用添加到理想量化器输入的 5 阶多项式直接调整我们的 ADC 模型。

我们的新 ADC 模型描述

我们上一篇文章中介绍的模型没有产生任何明显的杂散频率（杂散）。由于杂散是ADC性能的一个重要特征，因此需要更好的模型。

如图 1 所示。

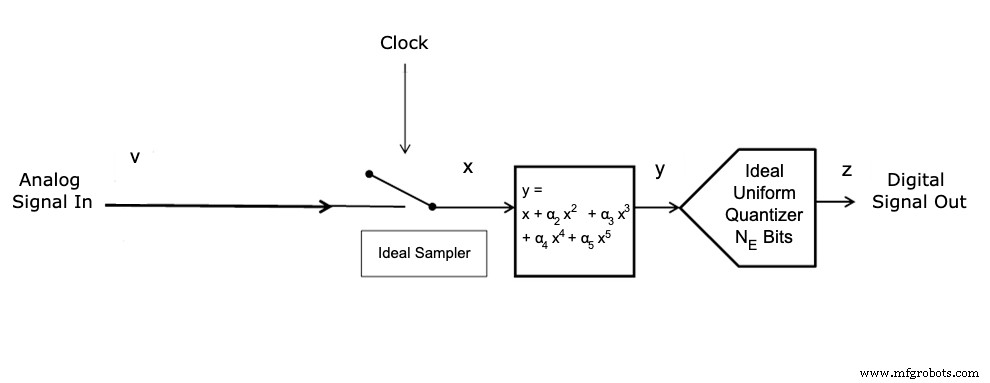
图 1.

这将一个 5 阶多项式添加到理想量化器输入中。

应使用双音输入来确定参数 αi(fc) 和 NE(fc)；其中 fc 是音调之间的中心频率，如图 2 所示（您将在我们的第一篇文章中将其识别为图 4）。

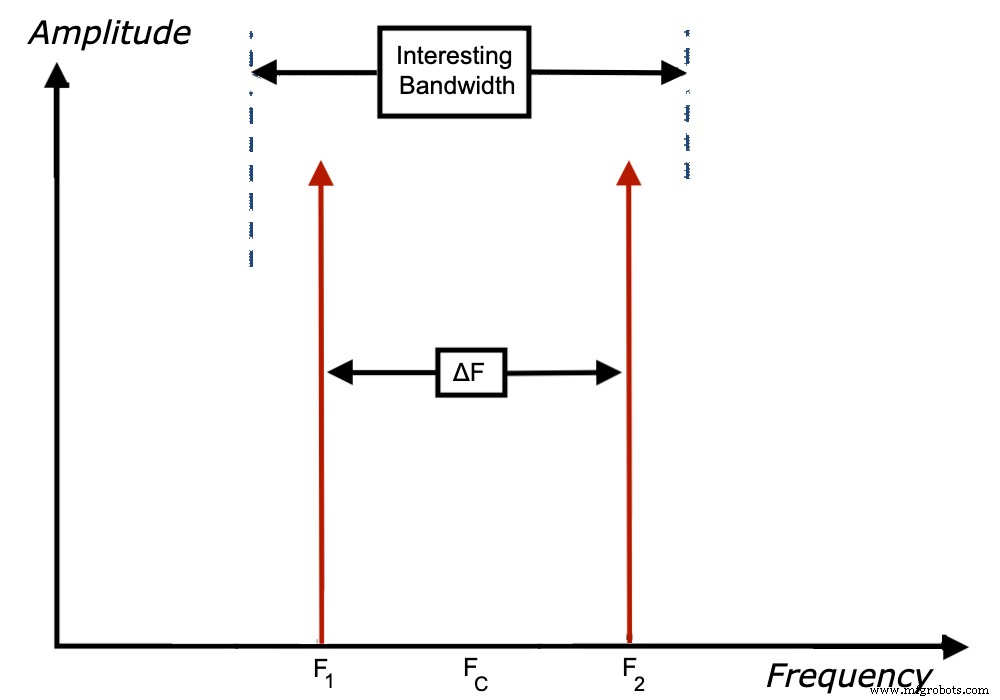
图 2.

如果这些参数中的任何一个也是 Δf（音调之间的间隔）的函数，则 ADC 中的存储器可能存在非线性，并且该模型将不适用。

例如，使用了与图 3 相同的双音输入（在我们之前的文章中讨论为图 3），NE =8 位，α3 =0.04，所有其他αi =0。相同的奈奎斯特带宽(730.9 MHz) 和我们上一篇文章中的“有趣的带宽”(233.7 MHz) 存在。

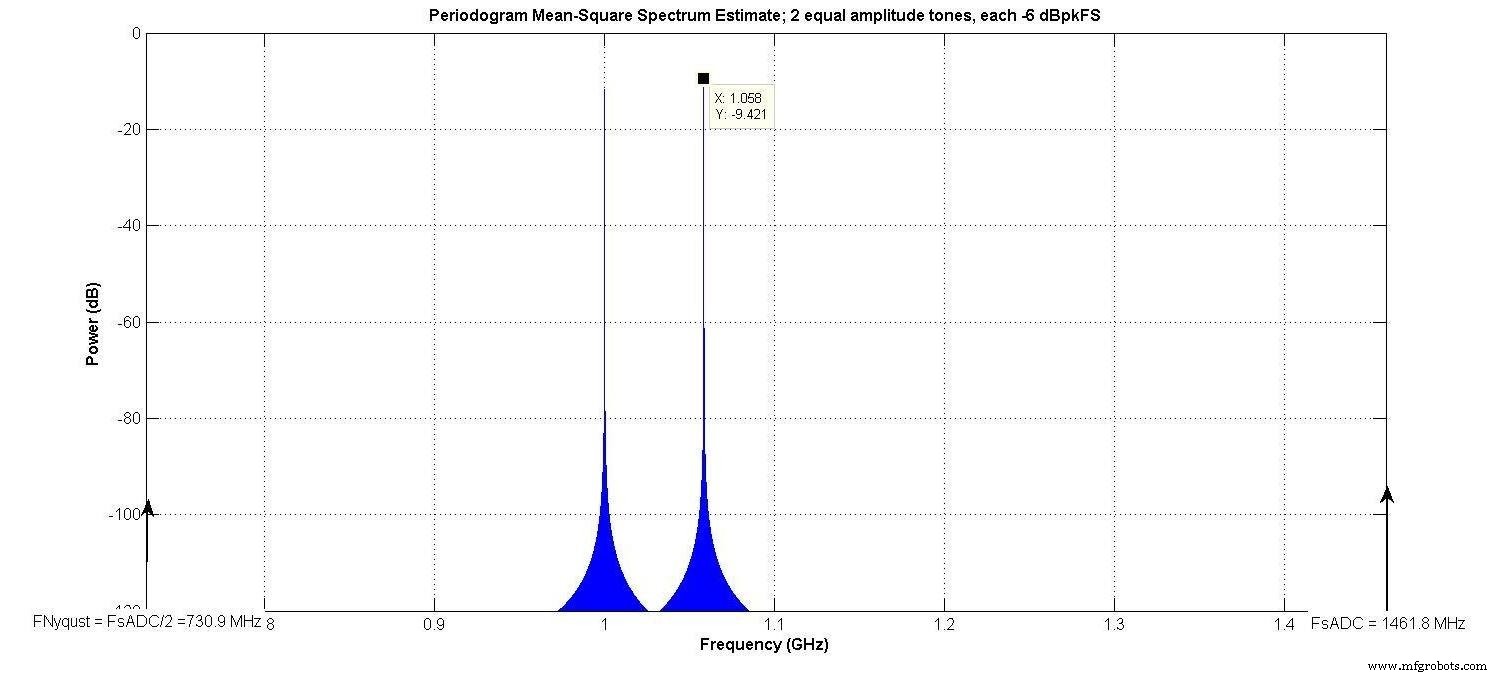
图 3。

图4为单音输入输出，图5为双音输入输出。

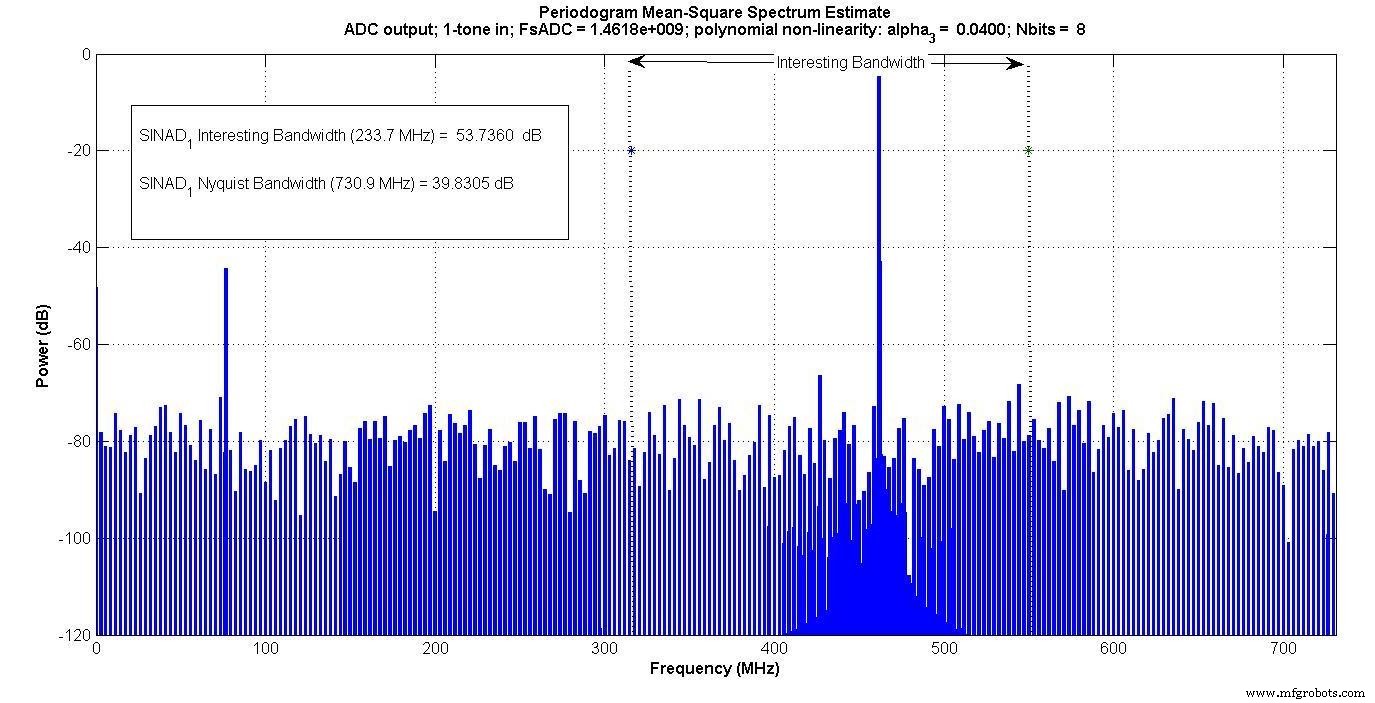
图 4。

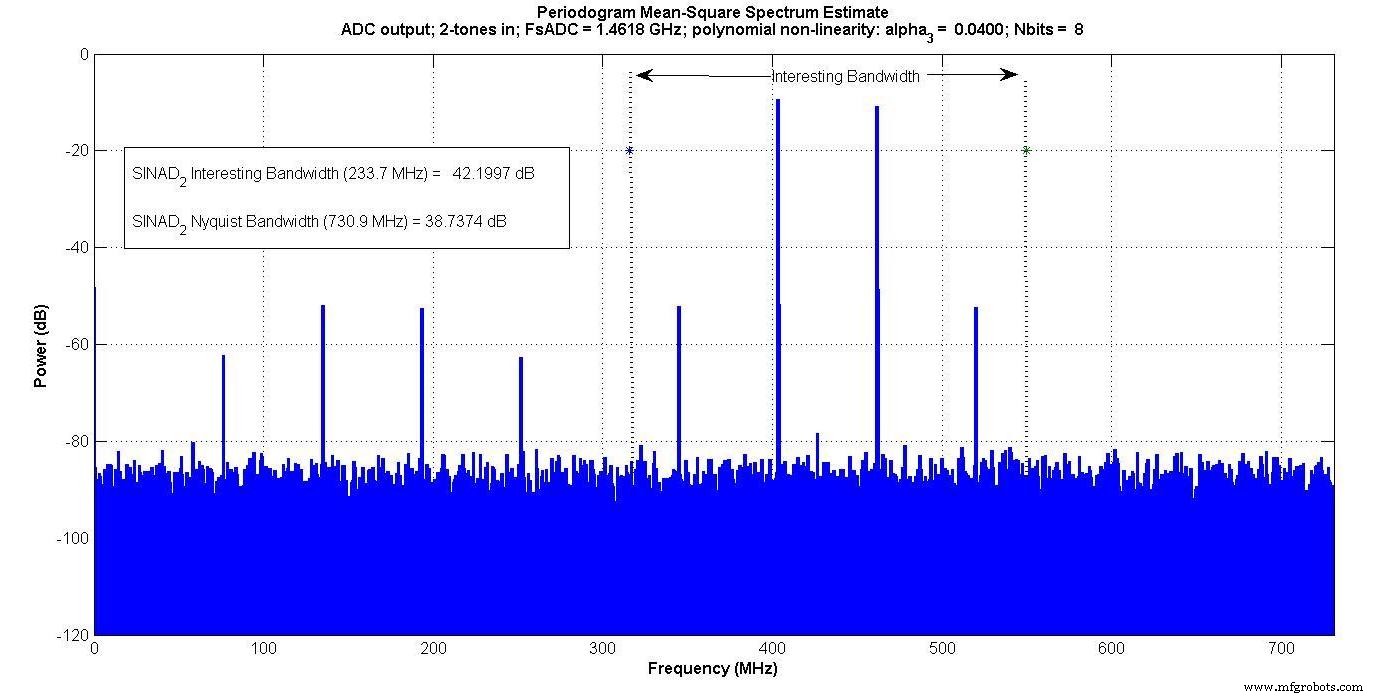
图 5。

互调产物出现在双音输入的“有趣带宽”内，但不出现在单音输入。

如果有人只在这个“有趣的带宽”内进行测量——例如，如果有一个只能通过那个频段的数字带通滤波器——单音测试不会捕捉到互调效应，但双音会捕捉到。

图 6 绘制了 5 到 12 个输入位的各种 SINAD。很明显，在“有趣的带宽”中测量的单音输入没有捕捉到超过 7 位的互调效应。

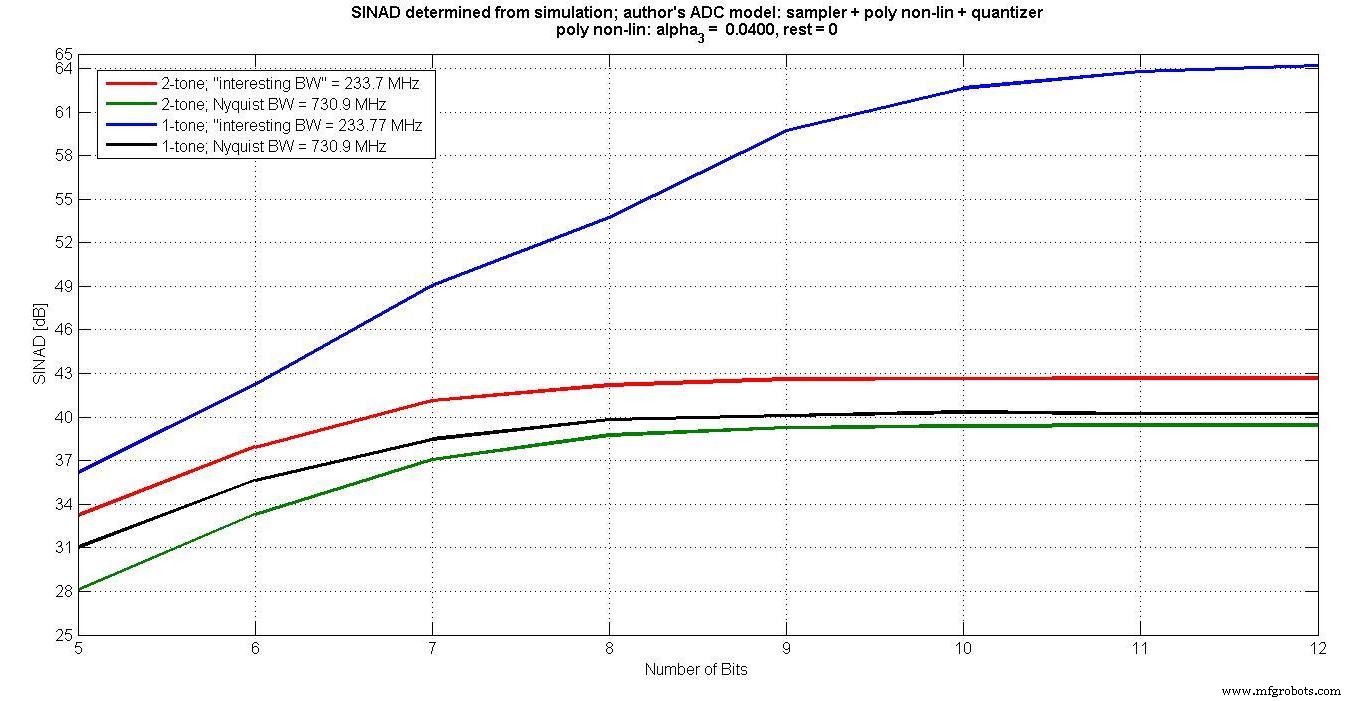
图 6。

此外，对于超过7位，由于量化噪声随着位数的增加而降低，但互调失真保持不变，SINAD并没有随着位数的增加而改善。

与制造商模型的比较

亲爱的读者：您现在可能想知道； “所以呢？这些只是一些模型及其对某些信号的响应。目的是什么？”

目的应该是可以对 ADC 进行双音测量，并选择图 1 中所示的参数值以最适合测量的 ADC 输出。这通常可以通过手动调整它们来完成，直到获得良好的配合。然后，简化模型可用于长误码率（BER）仿真。

测量可以在实际设备上、设备的良好模型上进行，也可以从制造商的数据表中获得。

要成为一个好的模型，它必须非常接近实际设备；例如完整的 SPICE 模型。如此复杂的模型在 BER 仿真中运行时间太长。

您的作者从制造商那里获得的是他们所谓的“行为”模型，他们声称该模型捕获了特定模型 ADC 的所有重要参数。制造商的模型还考虑了内部和外部时钟抖动。这是用来评估该方法的。

双音输入

图 7 显示了模拟设置。生成了双音输入，然后输入到您的作者和制造商的模型中。两者都用光谱分析显示。

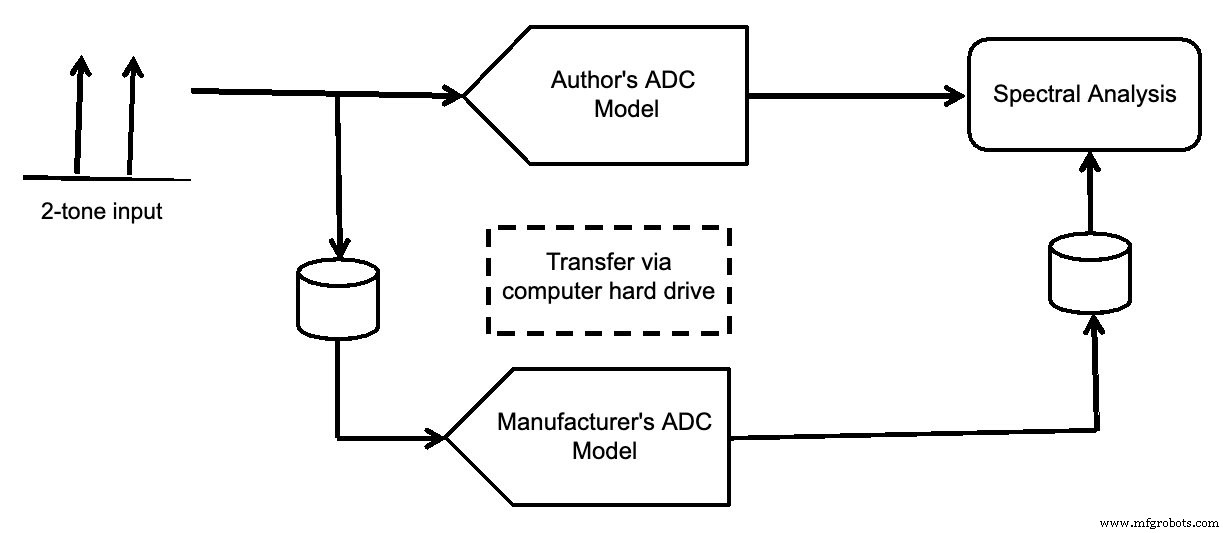
图 7。

图 8 显示了使用的输入。这两种音调在 300 到 350 MHz 之间。 ADC 采样频率约为 250 MHz，因此这些音调位于第三奈奎斯特区。

由于每个都在-6.02 dBpeakFS，当它们同相添加时，电压将增加两倍，导致0 dBpeakFS。

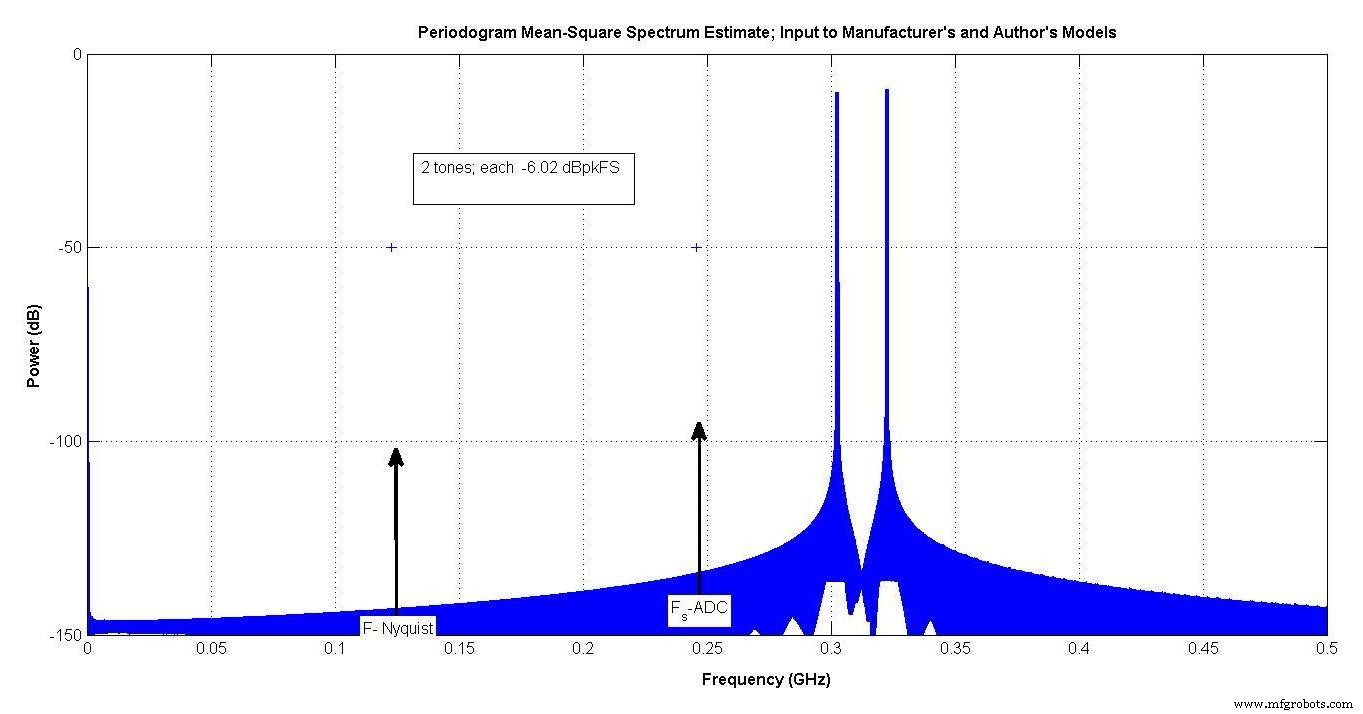
图 8。

图 9 显示了制造商模型的输出，该模型在大约 27 到 107 MHz 的“有趣带宽”中的 SINAD 为 63.74 dB。

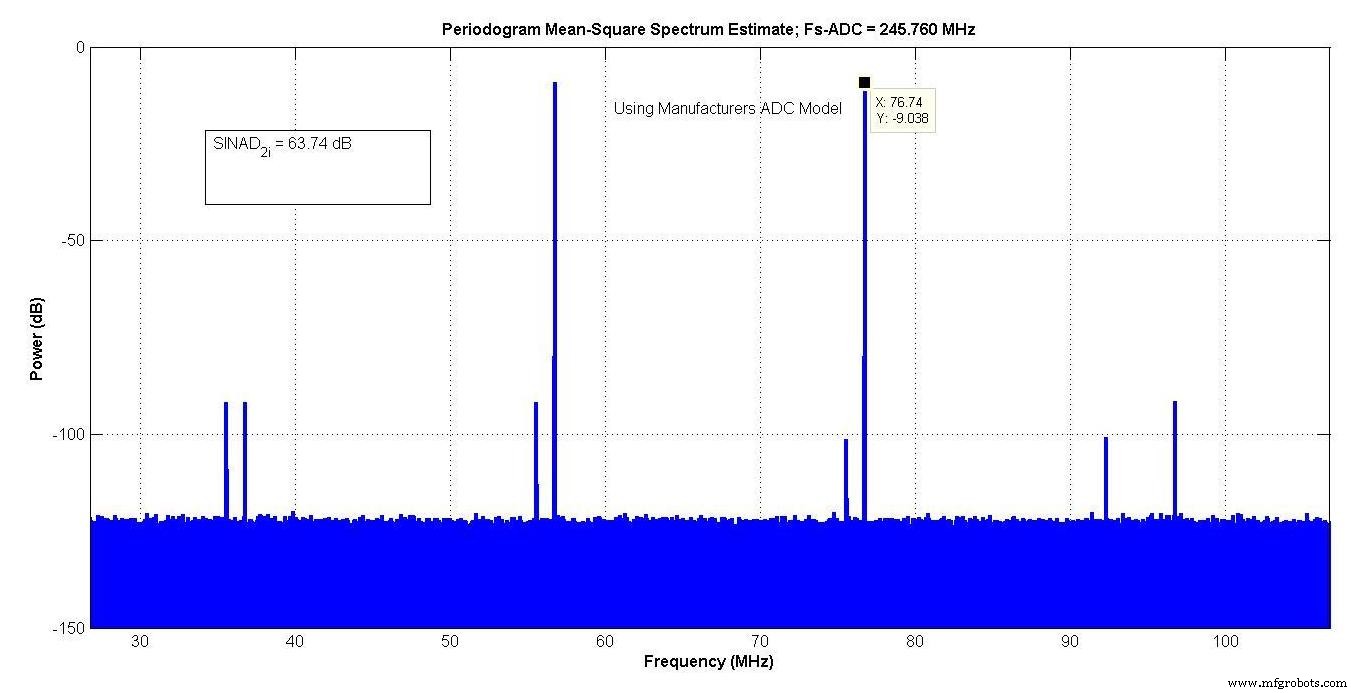
图 9.

图 10 显示了为匹配调整作者的模型参数后的结果。

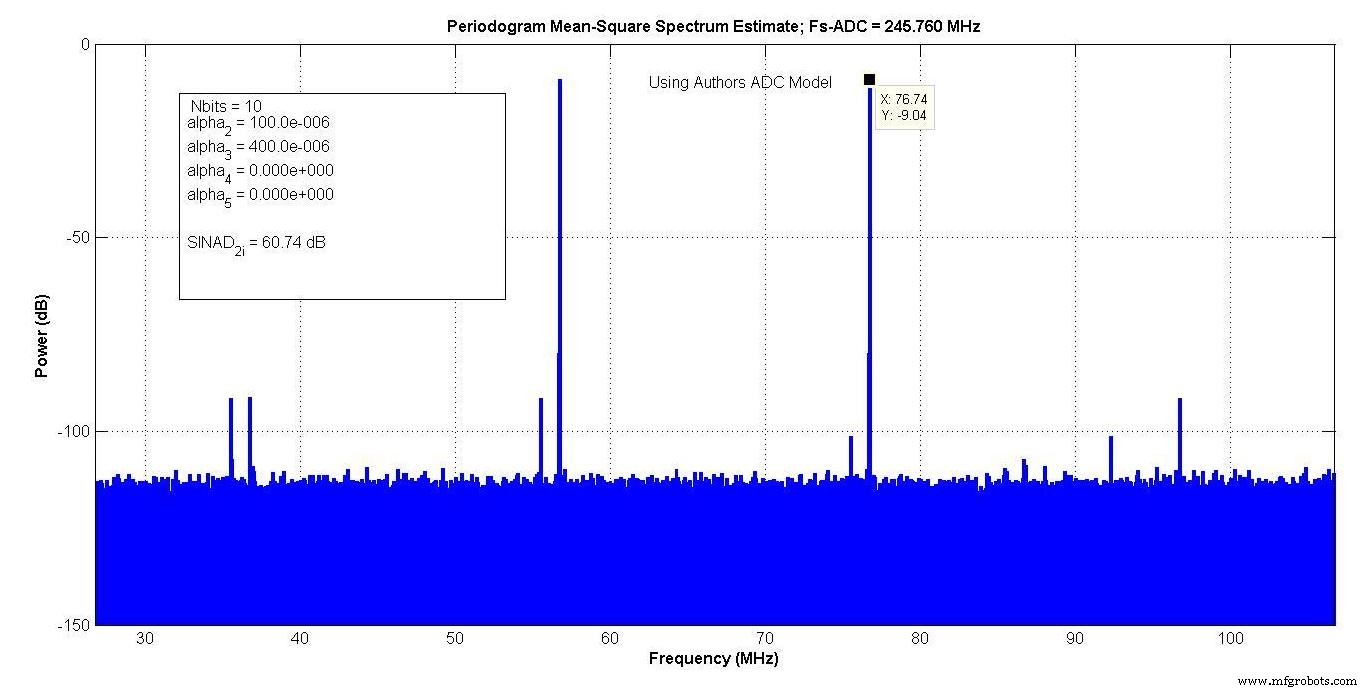
图 10.

多项式系数提供了足够的自由度，因此可以对杂散进行几乎精确的匹配。 11 位 NE 比制造商型号低 3 dB，10 位 NE 比制造商型号高 3 dB。

您的作者决定使用 10 位的悲观值，得出的 SINAD 为 60.74 dB。改进的模型将允许添加高达 6 dB 的附加高斯白噪声，因此可以选择较高的 NE 值，并添加附加噪声以匹配本底噪声。

OFDM 波形输入

现在可以将这两种模型以通信波形作为输入进行比较。

商用软件包附带LTE模型；产生一个OFDM信号。该模型包括调制器、选频瑞利衰落信道、加性高斯白噪声和解调器。

可以在解调器前面插入ADC模型，评估ADC输出的频谱，以及OFDM信号的误差矢量幅度，如图11所示。

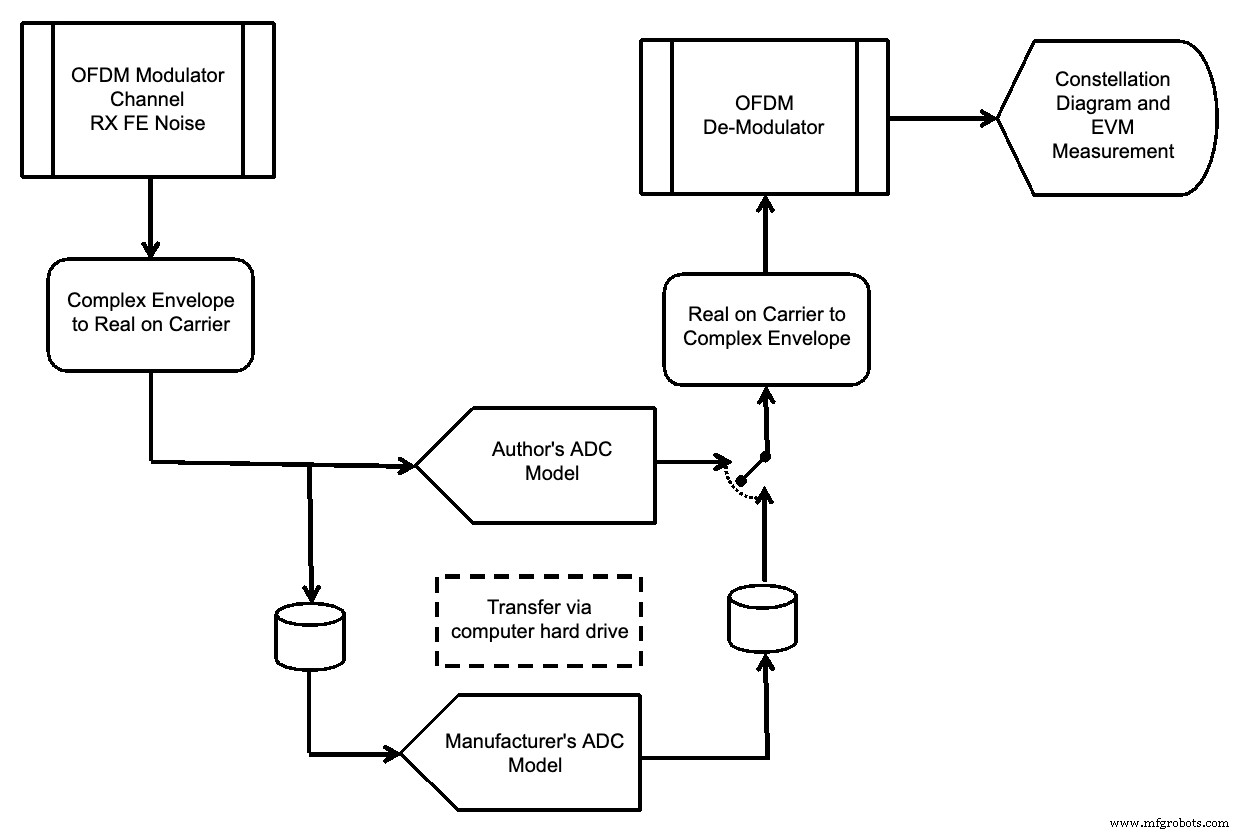
图 11。

使用了具有 64-QAM 子载波的 OFDM 信号。您作者的 ADC 模型参数与图 10 中使用的相同。

商用软件包使用复杂的包络符号 [3] 来形成其信号。这仅允许通过复数逐个样本地跟踪调制信息，并且载波频率仅保持为已知常数。因此，描述波形所需的样本数量大大减少。

但是，ADC 模型的输入需要是显式载波上的真实信号，以考虑作为输入频率函数的 ADC 性能差异。因此，需要完成“Complex Env​​elope to Real on Carrier”和“Real on Carrier to Complex Env​​elope”转换[3]。

图 12 显示了两种 ADC 模型的 OFDM 信号输入。它的中心频率与图 8 所示的两个音调相同。

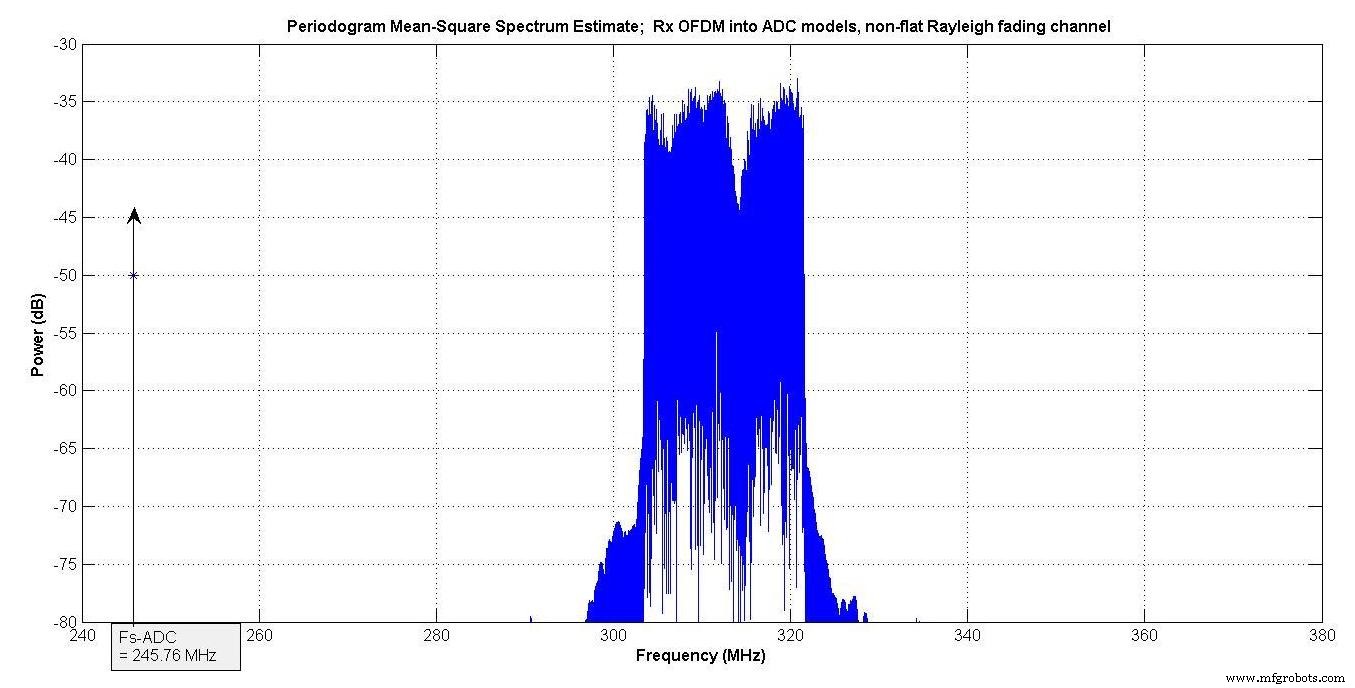
图 12.

两种 ADC 模型的 dBrmsFS 电平均为 -7 dBrmsFS。

图 13 显示了制造商模型的频谱，图 14 显示了您作者模型的频谱。由于 ADC 的非线性，两者都显示出频谱再生。光谱非常接近。

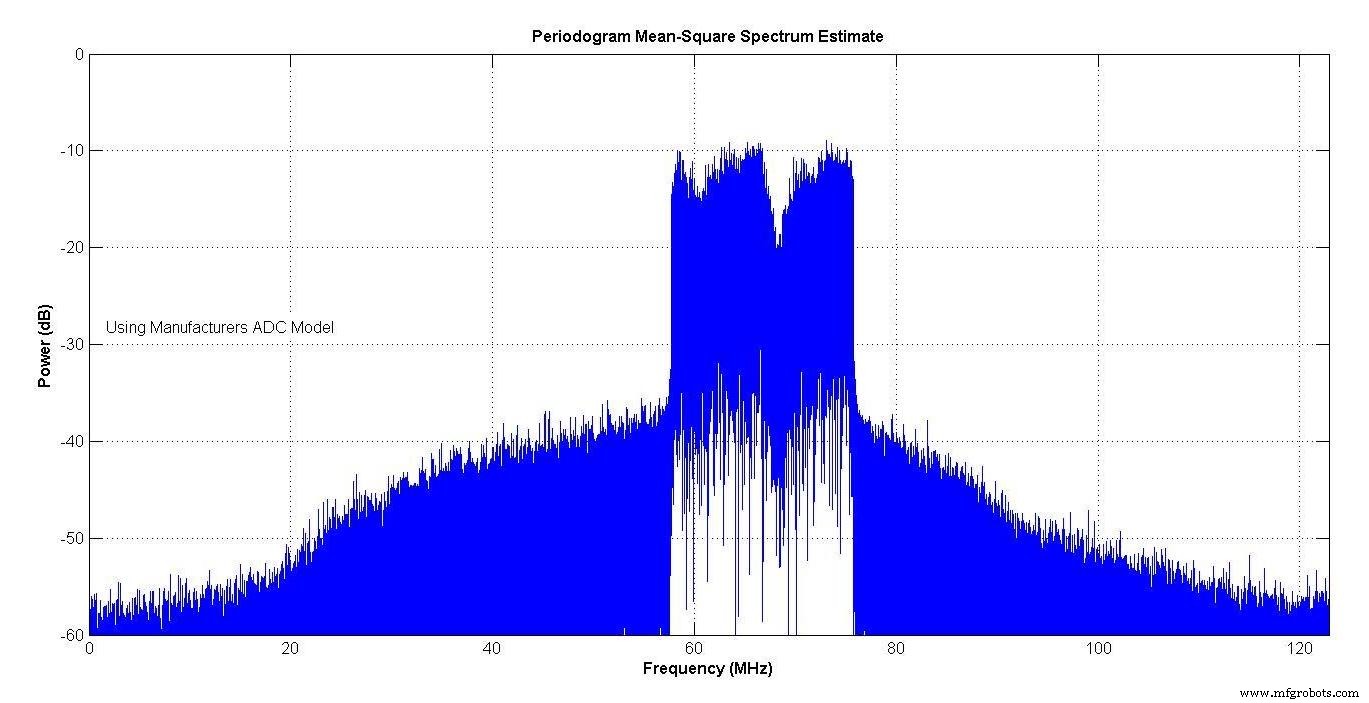
图 13。

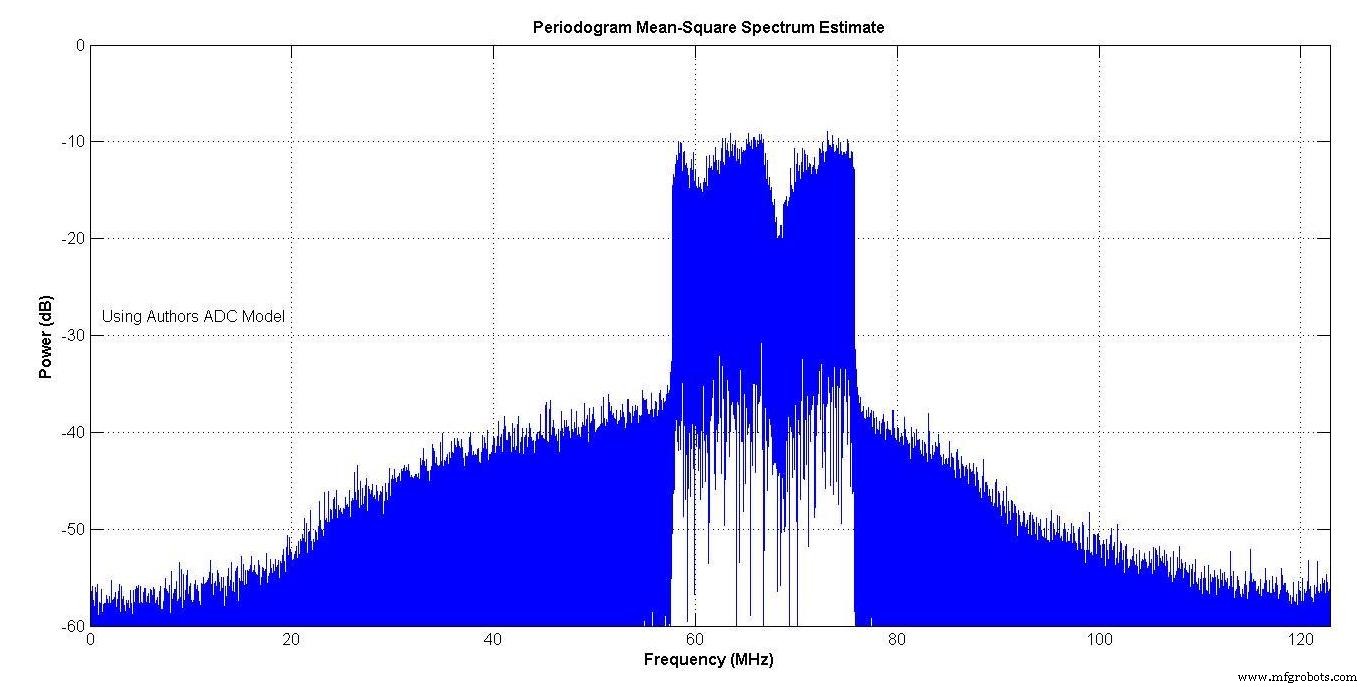
图 14。

图 15 显示了制造商模型的接收 OFDM 星座图，图 16 显示了您作者模型的星座图。

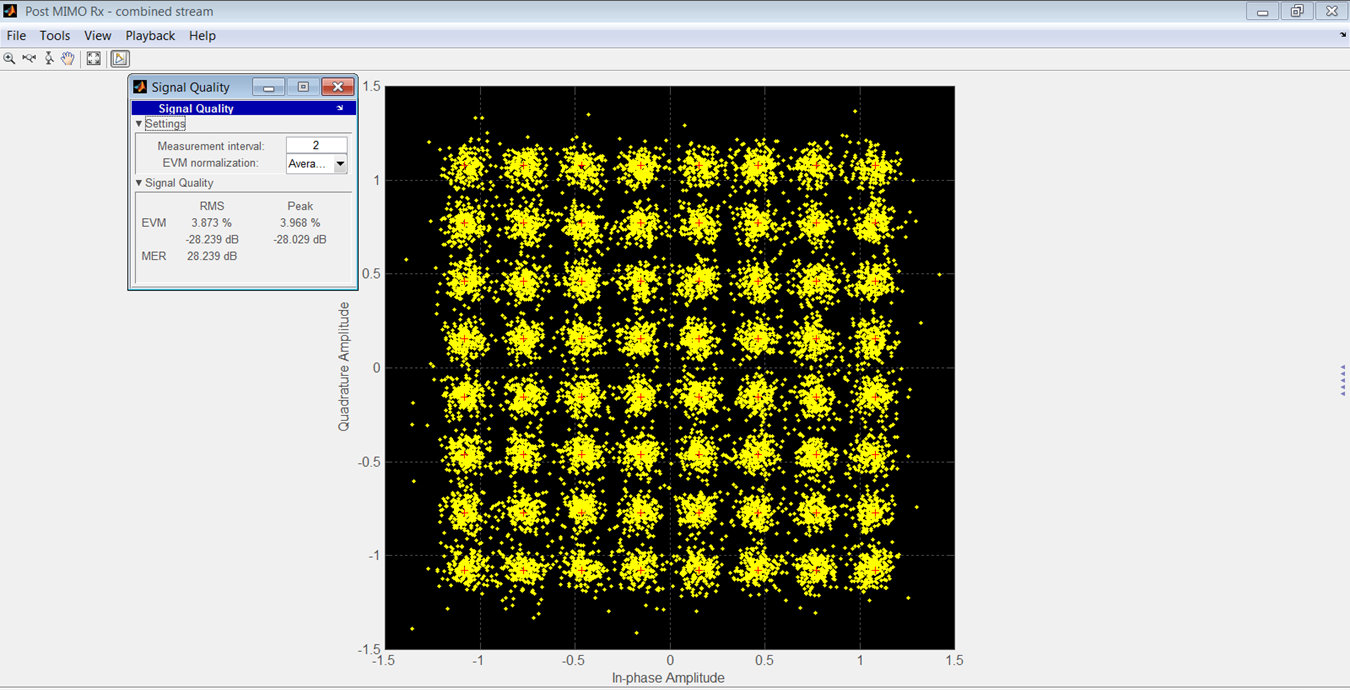
图 15。

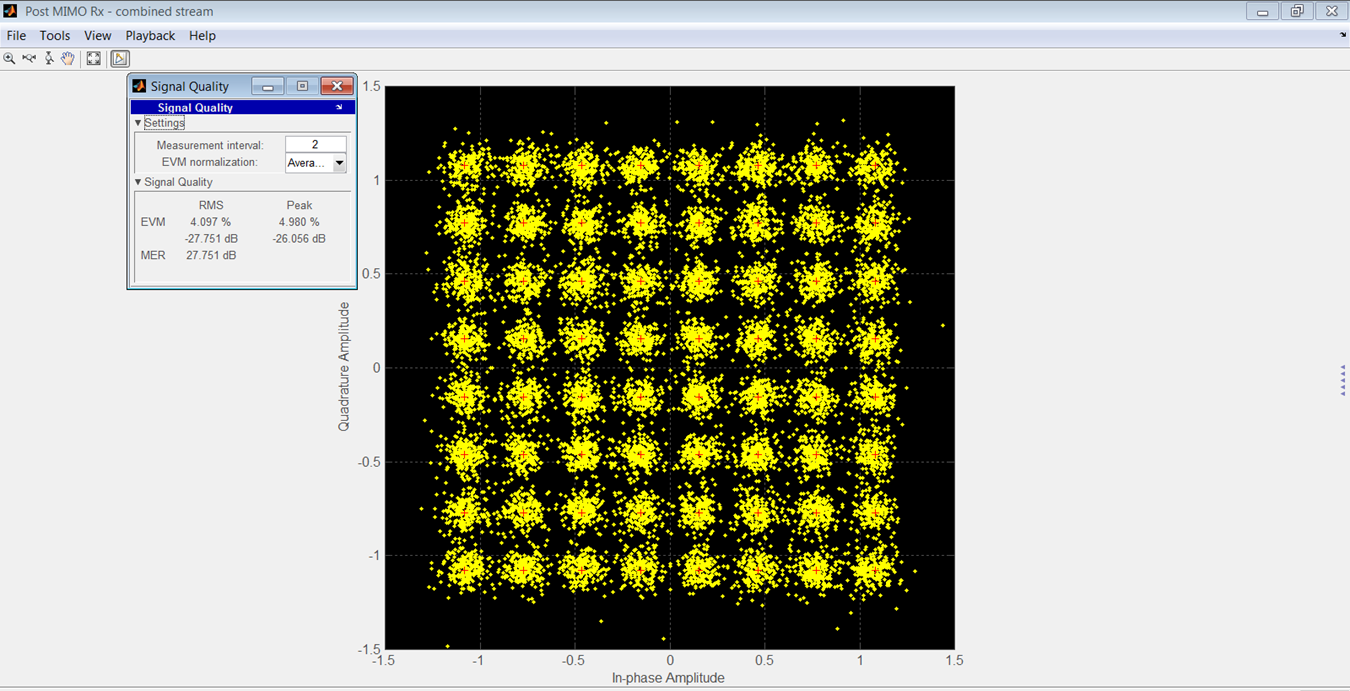
图 16.

rms 和峰值 EVM 的比较如表 3 所示。这些结果的 SNR 为 90 dB。

表 3。

在 -7 到 -47 dBrmsFS 的范围内，两种模型的 EVM 之间的 rms 差异为 3.46 dB。

总体而言，对于一组相当简单的参数，您的作者模型给出的结果与制造商的模型非常相似。没有关于制造商型号的信息，但它可能与您的作者相似。

在任何情况下，使用您作者的模型时模拟运行得更快，因为没有必要在模拟软件之间传输数据。因此，在图 17 所示的误码率 (BER) 仿真中使用了您作者的模型。

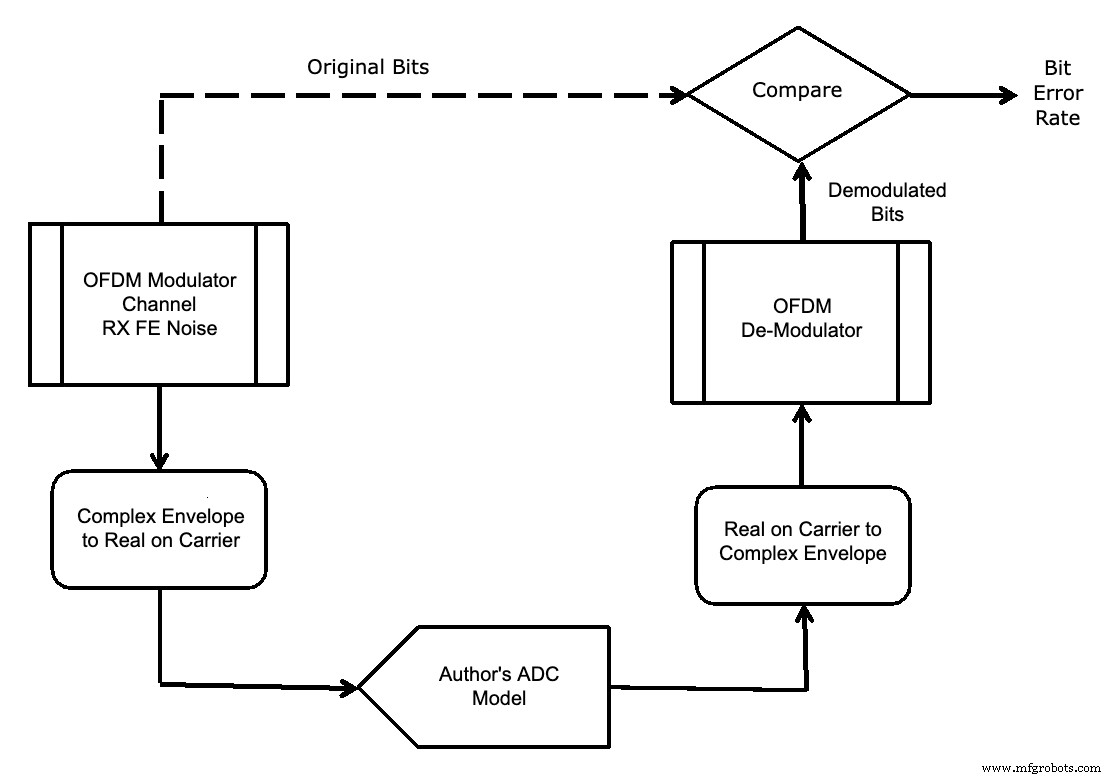
图 17.

设计带有 ADC 的系统时的一个重要参数是相对于 ADC 满量程放置信号的最佳电平。

电平太低导致信号相对于噪声和失真太小。

太高的电平会导致过度削波，这也会使信号失真。通常，允许一些剪辑的级别是最佳的。

三种不同 SNR 和 -41 至 -7 dBrmsFS 信号电平的 BER 如图 18 所示。

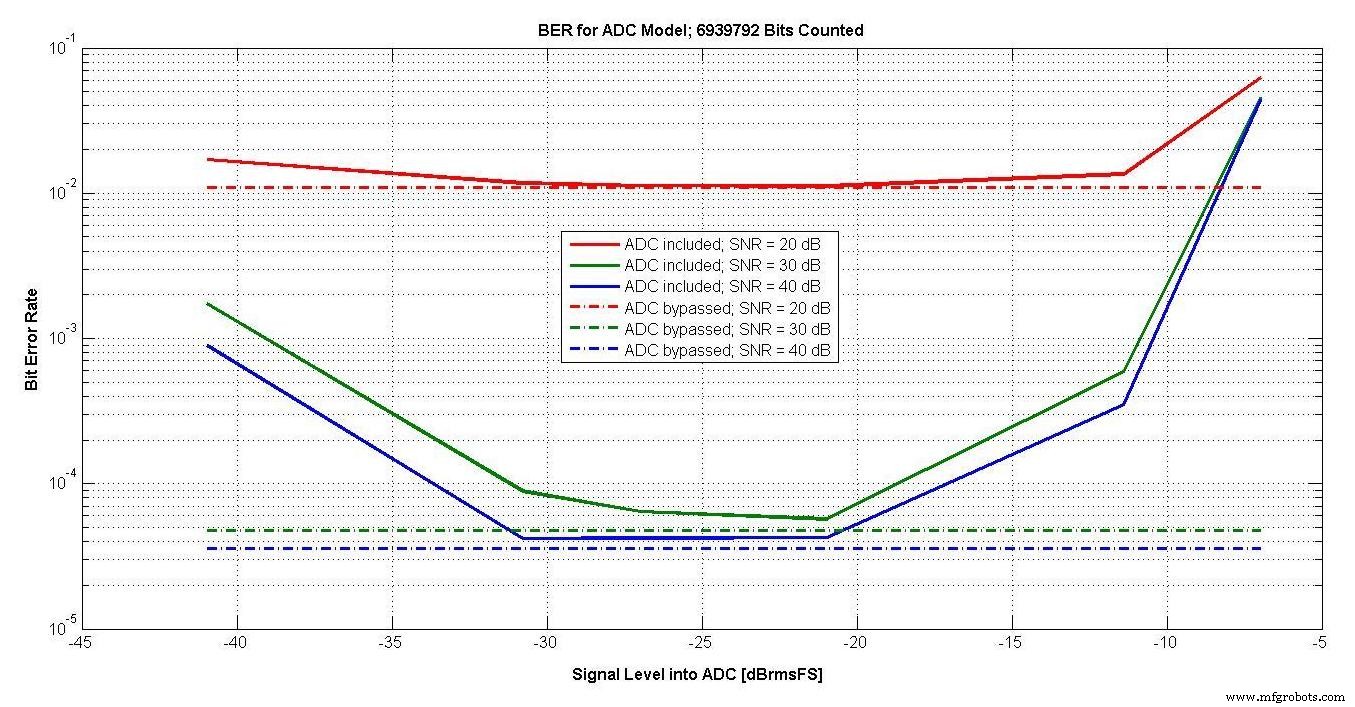
图 18。

还用虚线显示了绕过 ADC 模型时的 BER。对于 ADC，大约有 10 dB 的最佳范围，自动增益控制应将信号保持在此范围内。

---

在下一篇文章中，我们将通过对更好的模型的一些想法来结束本系列，并讨论一些关于 DAC 的模型。请在下面的评论中分享您对本系列的看法。