交流幅度的测量

到目前为止，我们知道交流电压极性交替，交流电流方向交替。我们也知道 AC 可以以各种不同的方式交替，通过跟踪随时间的交替，我们可以将其绘制为“波形”。

我们可以通过测量波在重复之前进化所需的时间（“周期”）来测量交替率，并将其表示为每单位时间的周期或“频率”。在音乐中，频率与音高相同 ，这是区分一个音符与另一个音符的基本属性。

然而，如果我们试图表达交流量的大小，就会遇到测量问题。使用直流电，电压和电流的量通常是稳定的，我们可以毫不费力地表示电路的任何部分有多少电压或电流。

但是，您如何对不断变化的事物进行单一的量级测量？

交流波形幅度的表示方法

表达强度或幅度（也称为幅度 )，一个交流量是在波形图上测量它的峰值高度。这被称为峰值 或冠 交流波形的值：下图

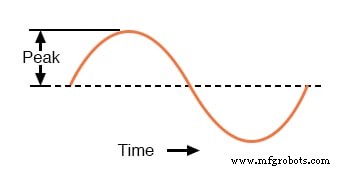
波形的峰值电压。

另一种方法是测量相对峰之间的总高度。这被称为峰峰值 交流波形的(P-P)值：下图

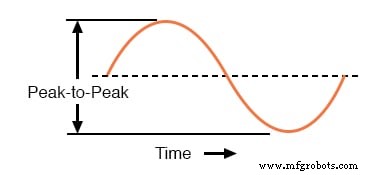
波形的峰峰值电压。

不幸的是，在比较两种不同类型的波时，这些波形幅度的表达中的任何一种都可能产生误导。例如，在 10 伏特处达到峰值的方波显然比在 10 伏特处达到峰值的三角波在更长时间内的电压量更大。

这两种交流电压为负载供电的效果会大不相同：下图

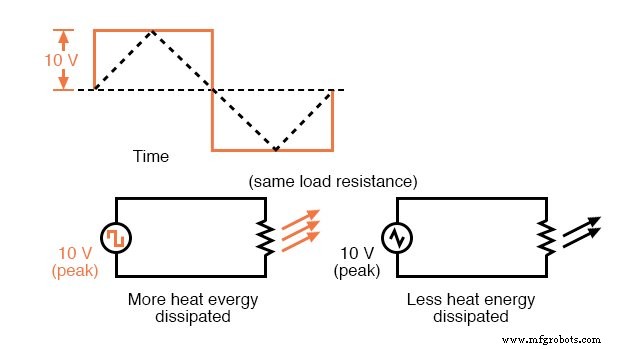
方波比相同的峰值电压三角波产生更大的热效应。

以更等效的方式表示不同波形的幅度的一种方法是将波形图上所有点的值在数学上平均为单个聚合数。这种幅度测量简单地称为平均值 波形的值。

如果我们对波形上的所有点进行代数平均（即考虑它们的符号 ，无论是正的还是负的），大多数波形的平均值在技术上为零，因为所有的正点在一个完整的周期内抵消了所有的负点：图下图

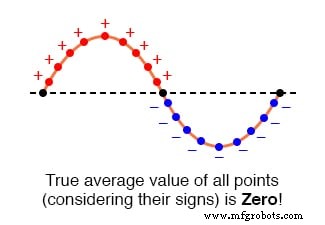
正弦波的平均值为零。

当然，这对于在绘图的“零”线上方和下方具有等面积部分的任何波形都适用。但是，作为实用 波形聚合值的度量，“平均值”通常定义为所有点的绝对值的数学平均值 一个循环。

换句话说，我们通过将波形上的所有点视为正量来计算波形的实际平均值，就好像波形是这样的：下图

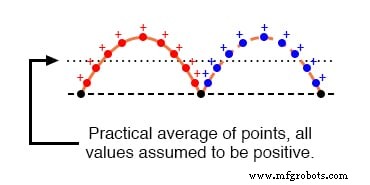
交流“平均响应”仪表看到的波形。

对极性不敏感的机械仪表运动（仪表设计为对交流电压或电流的正负半周做出同等响应）与波形的（实际）平均值成正比，因为指针对张力的惯性spring 自然地平均了随时间变化的电压/电流值产生的力。

相反，如果暴露于交流电压或电流，极性敏感的仪表运动会无用地振动，它们的指针在零标记附近快速振荡，表明对称波形的真实（代数）平均值为零。当本文中提及波形的“平均值”时，除非另有说明，否则将假定平均值是“实际”定义。

另一种导出波形幅度聚合值的方法是基于波形在应用于负载电阻时做有用功的能力。不幸的是，基于波形所做功的交流测量与该波形的“平均”值不同，因为功率 给定负载的耗散（单位时间所做的功）与施加在其上的电压或电流的大小不成正比。

相反，功率与平方成正比 施加到电阻上的电压或电流 (P =E ² /R, 并且 P =I ² R)。尽管这种幅度测量的数学计算可能并不简单，但它的实用性却是。

考虑一下带锯和拼图，这两种现代木工设备。两种类型的锯都使用薄的、带齿的、电动金属刀片来切割木材。但是，带锯使用刀片的连续运动来切割，而拼图则使用来回运动。

交流电（AC）与直流电（DC）的对比可以比作这两种锯片的对比：下图

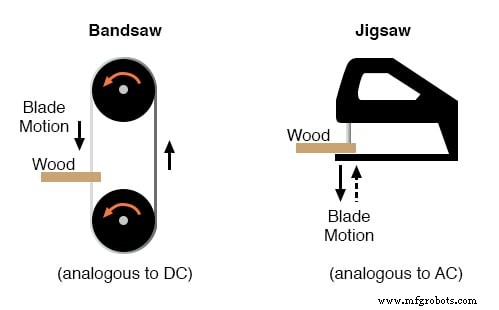
直流与交流的带锯-拼图类比。

在这个锯类类比中也存在试图在单个汇总测量中描述交流电压或电流的变化量的问题：我们如何表达拼图锯片的速度？带锯条以恒定速度移动，类似于直流电压推动或直流电流以恒定幅度移动的方式。另一方面，拼图刀片来回移动，其刀片速度不断变化。更重要的是，任意两把线锯的来回运动可能不是同一种类型，这取决于锯的机械设计。

一个拼图可能以正弦波运动移动其刀片，而另一个以三角波运动移动。根据其峰值对拼图进行评分 将一个拼图与另一个（或带有带锯的拼图）进行比较时，刀片速度会产生误导。尽管这些不同的锯以不同的方式移动刀片，但它们在一个方面是相同的：它们都切割木材，对这种共同功能的定量比较可以作为评估刀片速度的共同基础。

想象一个并排的拼图锯和带锯，配备相同的刀片（相同的齿距、角度等），同样能够以相同的速度切割相同类型的木材的相同厚度。我们可以说两把锯的切割能力相当或相等。这种比较是否可用于为线锯的前后刀片运动分配“等效带锯”刀片速度？将一种与另一种的木材切割效果联系起来？

这是用于将“直流等效”测量分配给任何交流电压或电流的一般想法：无论直流电压或电流的大小如何，都会通过相等的电阻产生相同数量的热能耗散：图下图

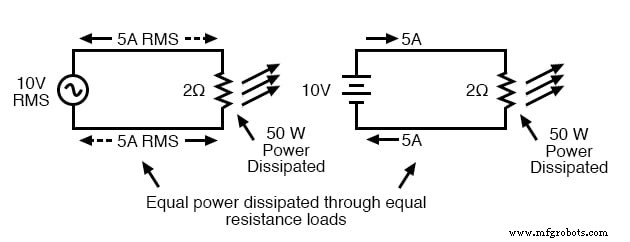
RMS 电压产生的热效应与 DC 电压相同

均方根 (RMS) 与 AC 有何关联？

在上面的两个电路中，我们有相同数量的负载电阻 (2 Ω)，以热量（50 瓦）的形式耗散相同数量的功率，一个由交流供电，另一个由直流供电。由于上图所示的交流电压源（就提供给负载的功率而言）相当于 10 伏直流电池，因此我们将其称为“10 伏”交流电源。

更具体地说，我们将其电压值表示为 10 伏 RMS .限定符“RMS”代表均方根 ，用于从图形上的点获得直流等效值的算法（本质上，该过程包括对波形图上的所有正负点进行平方，对这些平方值求平均值，然后取该平均值的平方根以获得最终答案）。

有时替代术语等价 或 DC 等价物 用“RMS”代替，但数量和原理都是一样的。

在处理电力测量时，RMS 幅度测量是将交流量与直流量或其他不同波形形状的交流量相关联的最佳方法。

出于其他考虑，最好采用峰值或峰峰值测量。例如，在确定将电力从电源传导到负载的适当尺寸（载流量）时，最好使用 RMS 电流测量，因为电流的主要问题是电线过热，这是一个函数电流通过导线电阻引起的功耗。

然而，在对用于高压交流应用的绝缘子进行评级时，峰值电压测量是最合适的，因为这里主要关注的是由短暂的电压尖峰引起的绝缘子“闪络”，而与时间无关。

用于测量波形幅度的仪器

峰值和峰峰值测量最好使用示波器，由于阴极射线管响应电压​​变化的快速动作，示波器可以高精度地捕获波形的波峰。对于 RMS 测量，模拟仪表运动（D'Arsonval、Weston、铁叶片、电测功机）只要在 RMS 数字中进行校准就可以工作。

因为机电仪表运动的机械惯性和阻尼效应使指针的偏转自然地与平均值成正比 AC 的值，而不是真正的 RMS 值，模拟仪表必须经过专门校准（或错误校准，具体取决于您如何看待它）以 RMS 单位指示电压或电流。

这种校准的准确性取决于假设的波形，通常是正弦波。

专为 RMS 测量设计的电子仪表最适合该任务。一些仪器制造商设计了巧妙的方法来确定任何波形的 RMS 值。一个这样的制造商生产的“真有效值”仪表带有一个由与被测电压成正比的电压供电的微小电阻加热元件。

该电阻元件的热效应是通过热测量来给出真实的 RMS 值的，无需任何数学计算，只是物理定律在实现 RMS 的定义。这种RMS测量的精度与波形无关。

峰值、峰峰值、平均值和 RMS 的关系

对于“纯”波形，存在简单的转换系数，用于将峰值、峰峰值、平均值（实用，非代数）和 RMS 测量值彼此相等：

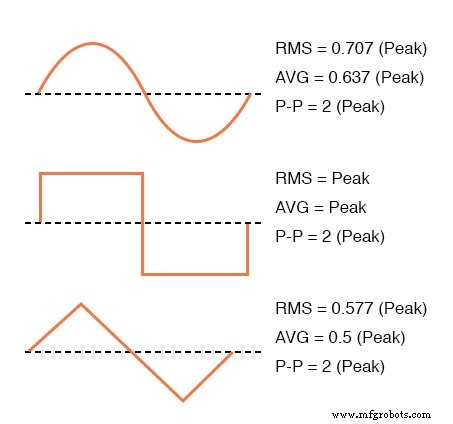
常见波形的转换系数。

除了交流波形的 RMS、平均值、峰值（波峰）和峰峰值测量之外，还有一些比率表示这些基本测量之间的比例。 波峰因数 例如，交流波形的峰值（波峰）值除以其均方根值的比值。

外形 AC 波形的 RMS 值除以其平均值的比率。方形波形的波峰和形状因子总是等于 1，因为峰值与 RMS 和平均值相同。正弦波形的 RMS 值为 0.707（2 的平方根的倒数），形状因子为 1.11（0.707/0.6​​36）。

三角形和锯齿形波形的 RMS 值为 0.577（3 的平方根的倒数），形状因子为 1.15（0.577/0.5）。

请记住，此处显示的正弦波、方波和三角波的峰值、RMS 和平均幅度的转换常数仅适用于 pure 这些波形的形式。畸变波形的均方根值和平均值不成比例关系：下图

任意波形没有简单的转换。

当使用模拟 D’Arsonval 仪表机芯测量交流电压或电流时，这是一个非常重要的概念。模拟 D'Arsonval 运动，经过校准以指示正弦波 RMS 幅度，只有在测量纯正弦波时才会准确。

如果被测电压或电流的波形不是纯正弦波，则仪表给出的指示将不是波形的真实 RMS 值，因为模拟 D'Arsonval 仪表运动中指针偏转的程度是与平均值成正比 波形的值，而不是 RMS。

RMS 仪表校准是通过“倾斜”仪表的跨度来获得的，因此它显示平均值的小倍数，这将等于特定波形的 RMS 值和仅特定波形 .

由于正弦波形在电气测量中最常见，因此它是模拟电表校准所假定的波形，用于电表校准的小倍数为 1.1107（外形系数：0.707/0.6​​36：RMS 除以正弦波形的平均值）。

除了纯正弦波之外的任何波形都将具有不同的 RMS 和平均值比率，因此针对正弦波电压或电流校准的仪表在读取非正弦波时将不会显示真正的 RMS。请记住，此限制仅适用于不采用“真有效值”技术的简单模拟交流电表。

评论：

• 幅度 交流波形的高度是其随时间变化的图表所描绘的高度。幅度测量可以采用峰值、峰峰值、平均值或 RMS 量的形式。
• 峰值 振幅是从零标记到图形上最高正或最低负点测量的交流波形的高度。也称为冠 波的振幅。
• 峰峰值 振幅是从图表上的最大正峰值到最大负峰值测量的 AC 波形的总高度。通常缩写为“P-P”。
• 平均 幅度是一个周期内所有波形点的数学“平均值”。从技术上讲，图形上“零”线上方和下方具有等面积部分的任何波形的平均幅度为零。然而，作为幅度的实际测量，波形的平均值通常被计算为所有点的绝对值的数学平均值 （取所有负值并将它们视为正值）。对于正弦波，如此计算的平均值约为其峰值的 0.637。
• “RMS”代表均方根 ，并且是用功能上等效于 DC 的术语来表示电压或电流的交流量的一种方式。例如，10 伏交流 RMS 是在给定值的电阻器上产生与 10 伏直流电源相同的热耗散量的电压量。也称为交流电压或电流的“等效”或“直流等效”值。对于正弦波，RMS 值约为其峰值的 0.707。
• 波峰因数 交流波形的峰值（波峰）与其 RMS 值的比值。
• 外形 交流波形的均方根值与其平均值的比值。
• 模拟机电仪表运动与平均值成比例响应 交流电压或电流的值。当需要 RMS 指示时，仪表的校准必须相应地“偏斜”。这意味着机电仪表 RMS 指示的准确度取决于波形的纯度：它是否与校准中使用的波形完全相同。

相关工作表：

• 基本示波器操作工作表