非线性传导

“通过回答问题取得进步。发现是通过质疑答案获得的。”

—Bernhard Haisch，天体物理学家

欧姆定律是一种简单而强大的数学工具，可以帮助我们分析电路，但它有局限性，我们必须了解这些局限性才能正确地将其应用到实际电路中。对于大多数导体来说，电阻是一种相当稳定的特性，在很大程度上不受电压或电流的影响。

为此，我们可以把很多电路元件的电阻看成一个常数，电压和电流是直接相关的。

例如，根据我们之前使用 3 Ω 灯的电路示例，我们通过将电压除以电阻 (I=E/R) 来计算通过电路的电流。使用 18 伏电池，我们电路的电流为 6 安培。将电池电压加倍至 36 伏，电流增加一倍，达到 12 安培。

当然，所有这些都是有道理的，只要灯继续为流过它的电流提供完全相同的摩擦（阻力）：3 Ω。

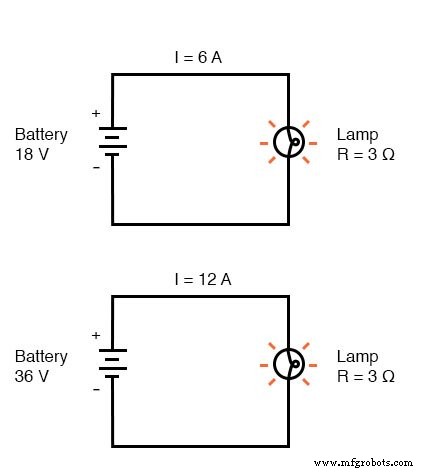
电阻变化时的电压-电流关系

然而，现实并非总是如此简单。在后面的章节中探讨的现象之一是导体电阻变化 与温度。在白炽灯中（利用电流将细细的灯丝加热到发出白热光的那种灯），随着从室温加热到工作温度，灯丝的电阻会急剧增加。

如果我们要增加实际灯电路中的电源电压，由此产生的电流增加会导致灯丝温度升高，从而增加其电阻，从而防止电流进一步增加而电池电压不会进一步增加.

因此，电压和电流不遵循简单的等式“I=E/R”（假设 R 等于 3 Ω），因为白炽灯的灯丝电阻对于不同的电流不会保持稳定。

电阻随温度变化而变化的现象是几乎所有金属都有的现象，大多数金属线都是由金属制成的。对于大多数应用，电阻的这些变化小到可以忽略不计。在金属灯丝的应用中，变化也是相当大的。

这只是电路中“非线性”的一个例子。这绝不是唯一的例子。数学中的“线性”函数是在图形上绘制时跟踪直线的函数。具有 3 Ω 恒定灯丝电阻的灯电路的简化版本生成如下图：

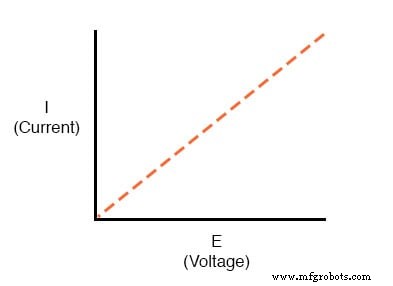
电流与电压的直线图表明电阻是一个稳定的、不变的值，适用于很宽的电路电压和电流范围。在“理想”情况下，情况就是这样。电阻器是为提供确定的、稳定的电阻值而制造的，其行为非常类似于上面看到的值图。数学家会称他们的行为为“线性”。

然而，对灯电路进行更现实的分析，在几个不同的电池电压值上会生成这样的图形：

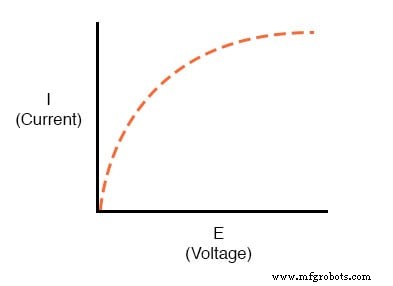
剧情不再是一条直线。随着电压从零增加到低电平，它在左侧急剧上升。随着它向右移动，我们看到线路变平，电路需要越来越大的电压增加以实现电流的相等增加。

如果我们尝试应用欧姆定律来找到具有上面绘制的电压和电流值的灯电路的电阻，我们会得到几个不同的值。我们可以说这里的阻力是非线性 ，随着电流和电压的增加而增加。非线性是由高温对灯丝金属线的影响引起的。

非线性电流传导的另一个例子是通过气体，例如空气。在标准温度和压力下，空气是一种有效的绝缘体。但是，如果由气隙隔开的两个导体之间的电压增大到足够大，间隙之间的空气分子就会被“电离”，它们的电子会被导线之间的高压力剥离。

一旦被电离，空气（和其他气体）成为电的良导体，允许电子在电离之前不存在的地方流动。如果我们像对灯电路那样在图表上绘制电流过电压，则电离的影响将被清楚地视为非线性：

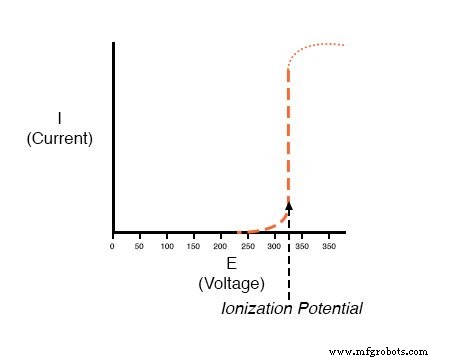
显示的图表是小气隙（小于一英寸）的近似值。更大的气隙会产生更高的电离电位，但 I/E 曲线的形状非常相似：在达到电离电位之前几乎没有电流，然后大量传导。

顺便说一下，这就是闪电以瞬时电涌而不是连续电子流的形式存在的原因。在空气电离足以支持大量电子流之前，地球和云之间（或不同组云之间）建立的电压必须增加到克服气隙电离电位的程度。

一旦这样做，电流将继续通过电离空气传导，直到两点之间的静电荷耗尽。一旦电荷耗尽，电压降至另一个阈值点以下，空气就会去离子化并恢复到其极高电阻的正常状态。

许多固体绝缘材料都表现出类似的电阻特性：在低于某个临界阈值电压时对电流具有极高的电阻，然后在超过该阈值的电压下电阻低得多。

一旦固体绝缘材料因高压击穿而受损 顾名思义，与大多数气体不同，它通常不会恢复到以前的绝缘状态。在低电压下可能会再次绝缘，但其击穿阈值电压会降低到较低的水平，这可能会导致将来更容易发生击穿。

这是高压接线常见的故障模式：击穿导致绝缘损坏。此类故障可以通过使用高压（1000 伏或更高）的特殊电阻计来检测。

具有非线性电阻的元件

有专门设计用于提供非线性电阻曲线的电路组件，其中之一是压敏电阻 .通常由氧化锌或碳化硅等化合物制成，这些器件在其端子之间保持高电阻，直到达到某个“点火”或“击穿”电压（相当于气隙的“电离电位”），此时他们的抵抗力急剧下降。

与绝缘体的击穿不同，压敏电阻击穿是可重复的：也就是说，它可以承受反复击穿而不会发生故障。此处显示了压敏电阻的图片：

还有一些特殊的充气管可以做同样的事情，利用与闪电电离空气中的工作原理完全相同的原理。

其他电气元件表现出比这更奇怪的电流/电压曲线。某些设备实际上会减少 电流随着施加电压的增加 .因为这种现象的电流/电压的斜率是负的（从左到右是向下而不是向上），所以它被称为负电阻 .

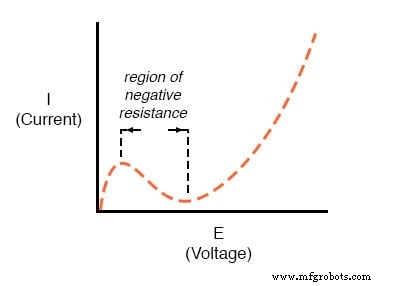
最值得注意的是，被称为四极管的高真空电子管 和称为 Esaki 的半导体二极管 或隧道 二极管在一定的外加电压范围内表现出负电阻。

欧姆定律对于分析电阻随电压和电流变化的元件的行为并不是很有用。甚至有人建议将“欧姆定律”从“定律”的地位降级，因为它不具有普遍性。将方程 (R=E/I) 称为电阻的定义可能更准确 , 适合某一类材料在较窄的条件范围内。

然而，为了学生的利益，我们将假设示例电路中指定的电阻是 除非另有说明，否则在很宽的条件下都是稳定的。我只是想让你了解一下现实世界的复杂性，以免给你一个错误的印象，即整个电气现象可以用几个简单的方程来概括。

评论：

• 大多数导电材料的电阻在各种条件下都是稳定的，但并非所有材料都如此。
• 任何可以在图形上绘制为直线的函数称为线性 功能。对于具有稳定电阻的电路，电流与电压的关系图是线性的 (I=E/R)。
• 在电阻随电压或电流变化而变化的电路中，电流与电压的关系图将非线性 （不是直线）。
• 一个压敏电阻 是一种随着施加在其上的电压量而改变电阻的组件。由于它的电压很小，它的电阻很高。然后，在某个“击穿”或“点火”电压下，其电阻会急剧下降。
• 负电阻 是通过组件的电流实际上随着其上施加的电压增加而减少的地方。一些电子管和半导体二极管（最著名的是四极管 管和江崎 , 或 隧道 二极管，分别）在一定的电压范围内表现出负电阻。

相关工作表：

• 负电阻工作表
• 电阻温度系数工作表