如何使用简单的感知器神经网络示例对数据进行分类
本文演示了感知器神经网络的基本功能并解释了训练的目的。
本文是感知器神经网络系列文章的一部分。
如果您想从头开始或继续前进,可以在此处查看其他文章:
- 如何使用神经网络进行分类:什么是感知器?
- 如何使用简单的感知器神经网络示例对数据进行分类
- 如何训练基本的感知器神经网络
- 了解简单的神经网络训练
- 神经网络训练理论简介
- 了解神经网络中的学习率
- 使用多层感知器进行高级机器学习
- Sigmoid 激活函数:多层感知器神经网络中的激活
- 如何训练多层感知器神经网络
- 了解多层感知器的训练公式和反向传播
- Python 实现的神经网络架构
- 如何在 Python 中创建多层感知器神经网络
- 使用神经网络进行信号处理:神经网络设计中的验证
- 训练神经网络数据集:如何训练和验证 Python 神经网络
什么是单层感知器?
在上一篇文章中,我们看到神经网络由分层排列的互连节点组成。输入层中的节点分发数据,其他层中的节点进行求和,然后应用激活函数。这些节点之间的连接是加权的,这意味着每个连接都将传输的数据乘以一个标量值。
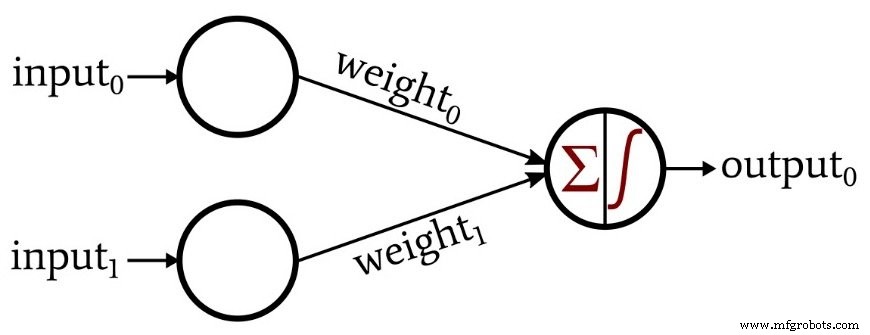
请注意,此配置称为单层感知器。是的,我知道,它有两层(输入和输出),但它只有一层包含计算节点。
用感知器分类
在本文中,我们将使用以下神经网络探索感知器功能。
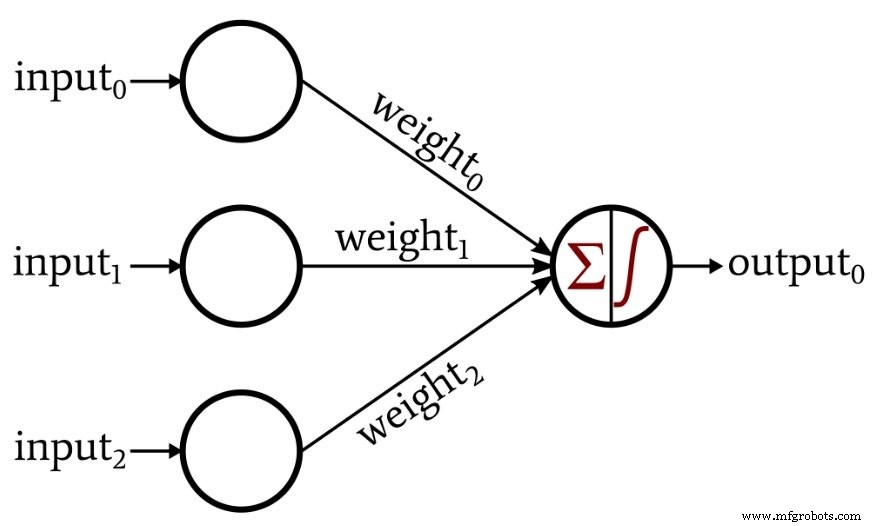
如您所见,我们的输入维度为 3。我们可以把这个感知器看作是解决三维空间问题的工具。例如,我们提出以下问题:如果三维空间中的一个点位于 x 轴下方,则它对应的数据无效。如果该点位于 x 轴上或上方,则它对应于必须保留以供进一步分析的有效数据。我们需要这个中性网络来对我们的数据进行分类,输出值为 1 表示有效数据,输出值为 0 表示无效数据。
首先,我们必须将我们的三维坐标映射到输入向量。在此示例中,input0 是 x 分量,input1 是 y 分量,而 input2 是 z 分量。接下来,我们需要确定权重。这个例子非常简单,我们不需要训练网络。我们可以简单地考虑所需的权重并分配它们:
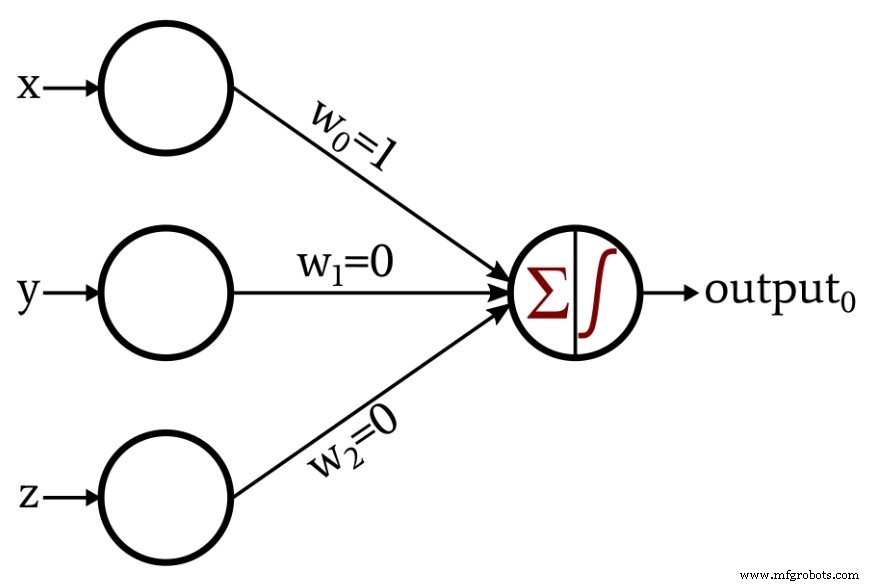
我们现在需要做的就是指定输出节点的激活函数是一个单位步长,表示如下:
\[f(x)=\begin{cases}0 &x <0\\1 &x \geq 0\end{cases}\]
感知器的工作方式如下:由于 w1 =0 和 w2 =0,y 和 z 分量对输出节点生成的总和没有贡献。唯一影响求和的输入数据是 x 分量,由于 w0 =1,它不加修改地传递到输出节点。如果三维空间中的点在 x 轴以下,则输出节点的求和将为负,并且激活函数会将此负值转换为output0 =0。如果三维空间中的点在x轴上或以上,则求和等于或大于零,激活函数会将其转换为output0 =1.
用感知器解决问题
在上一节中,我将我们的感知器描述为解决问题的工具。不过,您可能已经注意到,感知器并没有解决太多问题——我 解决了问题,并通过分配所需的权重将解决方案提供给感知器。
在这一点上,我们已经达到了一个关键的神经网络概念:我能够快速解决有效/无效分类问题,因为输入数据和所需输出值之间的关系非常简单。然而,在许多现实生活中,人类很难在输入数据和输出值之间建立数学关系。 我们可以获取输入数据,我们可以记录或产生相应的输出值,但是我们没有从输入到输出的数学路径。
一个有用的例子是手写识别。假设我们有手写字符的图像,我们想将这些图像分类为“a”、“b”、“c”等,以便我们可以将手写体转换为普通的计算机文本。任何知道如何书写和阅读的人都能够生成输入图像,然后为每个图像分配正确的类别。因此,收集输入数据和相应的输出数据并不困难。另一方面,查看输入输出对并制定数学表达式或算法将输入图像正确转换为输出类别将非常困难。
因此,手写识别和许多其他信号处理任务提出了人类在没有复杂工具的帮助下无法解决的数学问题。尽管神经网络无法思考、分析和创新,但它们使我们能够解决这些难题,因为它们可以做人类无法做到的事情——即快速、重复地执行涉及潜在海量数值数据的计算.
训练网络
允许神经网络创建从输入到输出的数学路径的过程称为训练。我们给出由输入值和相应输出值组成的网络训练数据,并对这些值应用固定的数学程序。此过程的目标是逐步修改网络的权重,以便网络即使使用以前从未见过的输入数据也能计算出正确的输出值。它本质上是在训练数据中寻找模式并生成权重,通过将这些模式应用于新数据来产生有用的输出。
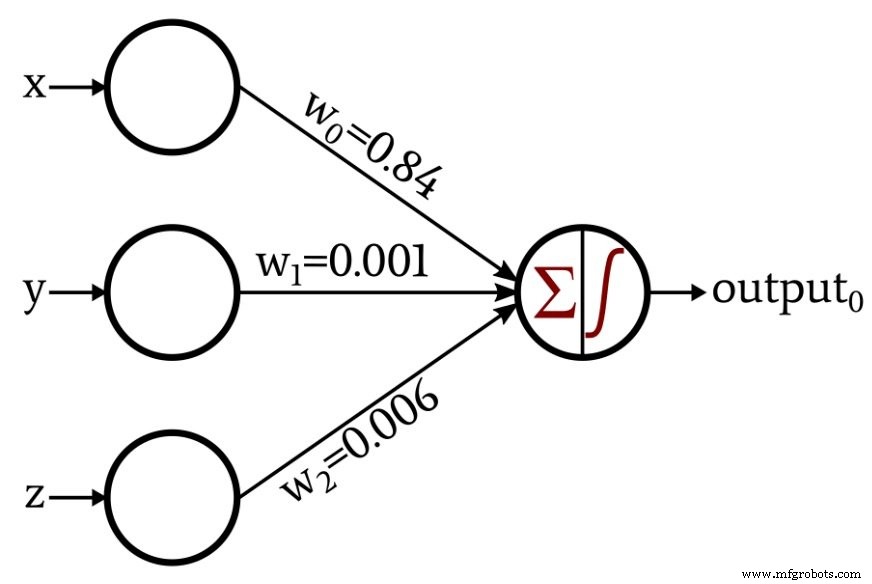
下图显示了上面讨论的有效/无效分类器,但权重不同。这些是我通过用 1000 个数据点训练感知器生成的权重。如您所见,训练过程使感知器能够自动逼近我通过人类式批判性思维确定的数学关系。
在下一篇文章中......
我已经向你展示了训练这个感知器的结果,但我没有说我是如何获得这些结果的。下一篇文章将描述一个实现单层感知器神经网络的简短 Python 程序,我还将解释我的训练过程。
嵌入式


