分贝

Bel 用于表示增益

在最简单的形式中，放大器的增益 是产出与投入的比率。像所有比率一样，这种形式的增益是无单位的。然而，有一个实际的单位用来表示增益，它被称为 bel .

作为一个单位，贝尔实际上被设计为一种方便的方式来表示功率损失 在电话系统布线而不是增益 在放大器中。该单位的名称源自苏格兰著名发明家亚历山大·格雷厄姆·贝尔（Alexander Graham Bell），他的工作在开发电话系统方面发挥了重要作用。最初，bel 表示由于标准长度的电缆上的电阻引起的信号功率损失量。现在，它是根据功率比（输出功率除以输入功率）的常用（以 10 为底）对数来定义的：

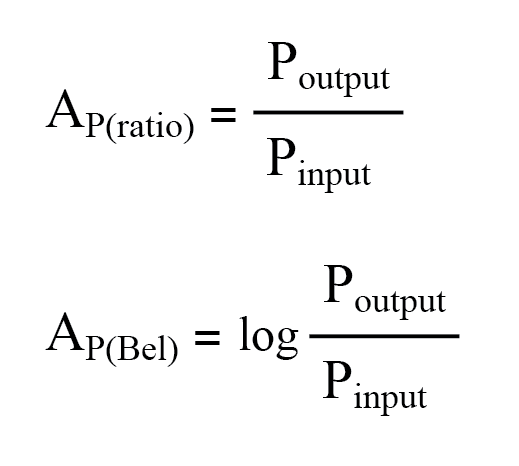
Bel 是非线性的

因为bel是一个对数单位，所以它是非线性的。为了让您了解其工作原理，请考虑下表，比较了以 bels 为单位的功率损耗和增益与简单比率：

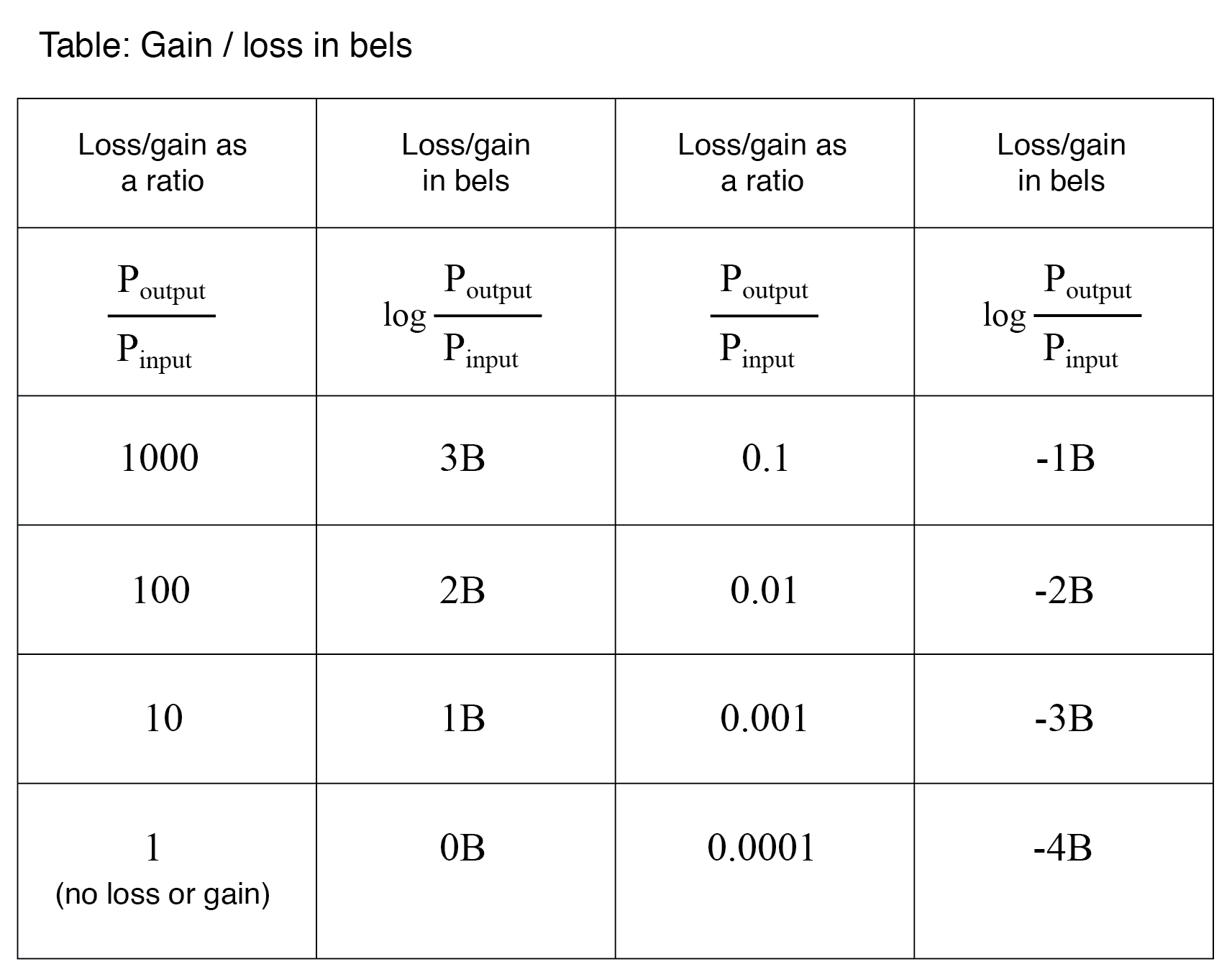
从贝尔到分贝

后来认为 bel 是一个太大的单位而不能直接使用，因此习惯上使用公制前缀 deci （意思是 1/10），使它deci 贝尔，或分贝。现在，“dB”这个词太常见了，以至于很多人都没有意识到它是“deci-”和“-bel”的组合，甚至没有意识到“bel”这样的单位。从这个角度来看，这是另一个对比功率增益/损耗比与分贝的表格：

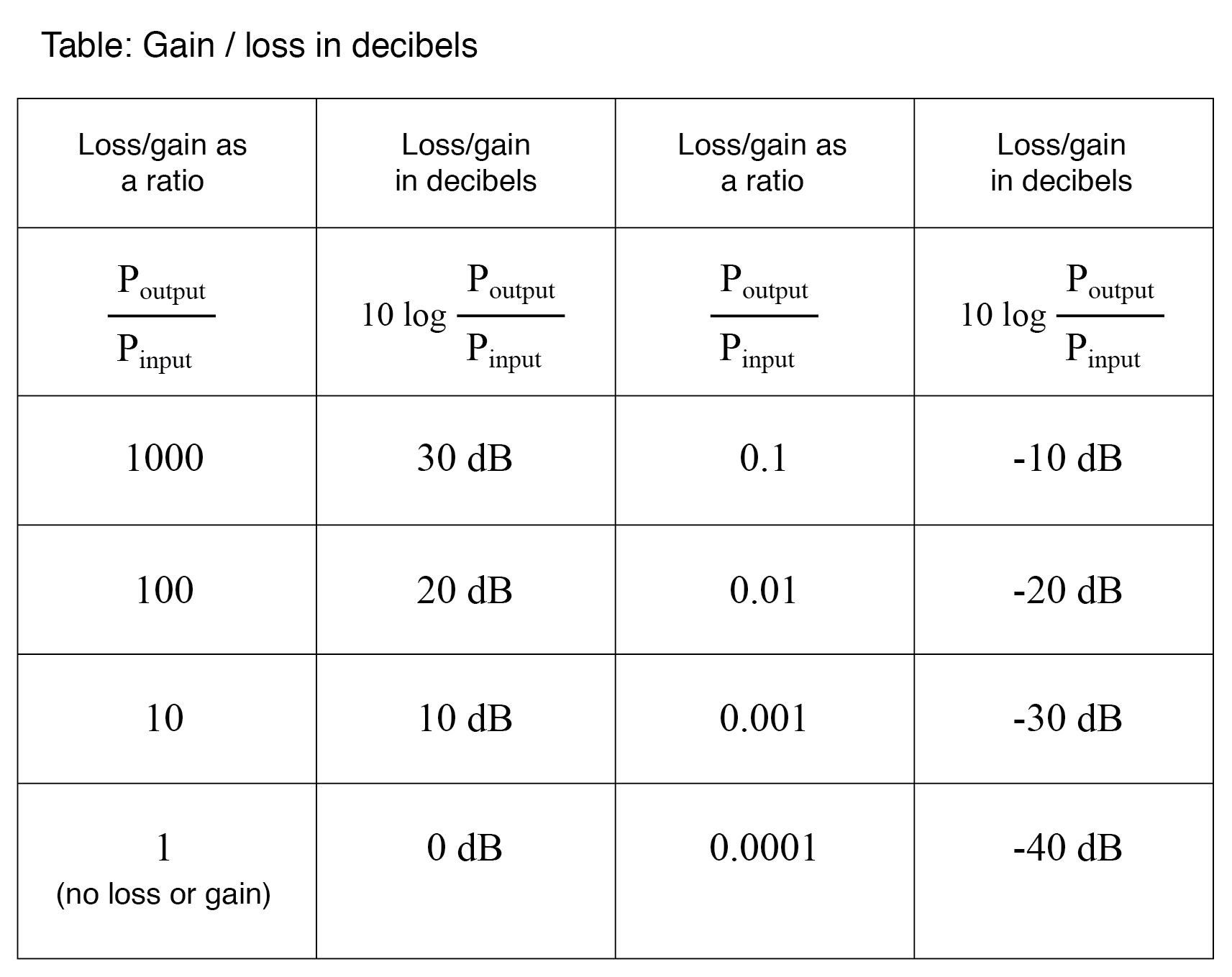
作为对数单位，这种功率增益表达模式涵盖了广泛的比率范围，并且数字跨度最小。可以合理地问，“为什么有人觉得有必要发明一个对数 电话系统中电信号功率损耗的单位？”答案与人类听觉的动力学有关，其感知强度本质上是对数的。

人类听觉是非线性的

人类的听觉是高度非线性的：为了使声音的感知强度加倍，实际声功率必须乘以 10 倍。在这种情况下，用对数“bel”标度来关联电话信号功率损耗非常有意义：1 bel 的功率损耗转化为 50% 或 1/2 的感知声音损耗。 1 贝尔的功率增益转化为声音感知强度的两倍。

其他对数刻度示例：里氏刻度和化学 pH 值

里氏音阶

与贝尔震级几乎完美的类比是用来描述地震强度的里氏震级：里氏 6.0 级地震的强度是里氏 5.0 级地震的 10 倍；里氏 7.0 级地震的威力是里氏 5.0 级地震的 100 倍；里氏 4.0 级地震的强度是里氏 5.0 级地震的 1/10，依此类推。

化学 pH 值

化学 pH 值的测量尺度同样是对数的，尺度上的差异 1 相当于化学溶液中氢离子浓度的十倍差异。使用对数测量尺度的一个优势是相对较小的数值跨度提供了巨大的表达范围，正是这种优势确保了地震使用里氏数和氢离子活动的pH值。

使用 Bel 表达系统得失

采用贝尔作为增益单位的另一个原因是为了简单表达系统的损益。考虑最后一个系统示例（上图），其中两个放大器串联连接以放大信号。每个放大器各自的增益表示为一个比率，系统的整体增益是这两个比率的乘积（相乘）：

总增益 =(3)(5) =15

如果这些数字代表了力量 增益，我们可以直接将贝尔单位应用于表示每个放大器以及整个系统的增益的任务。 （下图）

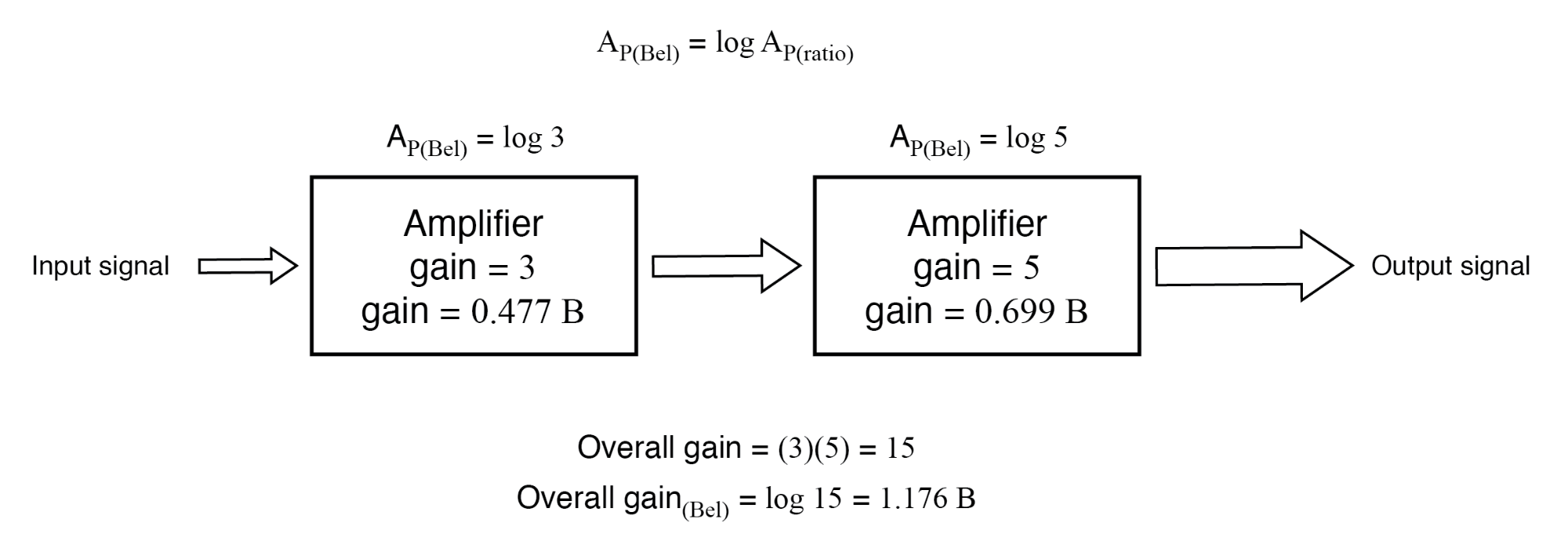
以贝尔为单位的功率增益是相加的：0.477 B + 0.699 B =1.176 B。

仔细检查以“bel”为单位的这些增益数字会产生一个发现：它们是可加的。比增益数字是分级放大器的乘法，但增益以 bels add 表示 而不是乘以 等于整个系统增益。功率增益为 0.477 B 的第一个放大器加上第二个放大器的 0.699 B 功率增益，使系统的总功率增益为 1.176 B。

使用分贝的增益

重新计算分贝而不是贝尔，我们注意到同样的现象。 （下图）

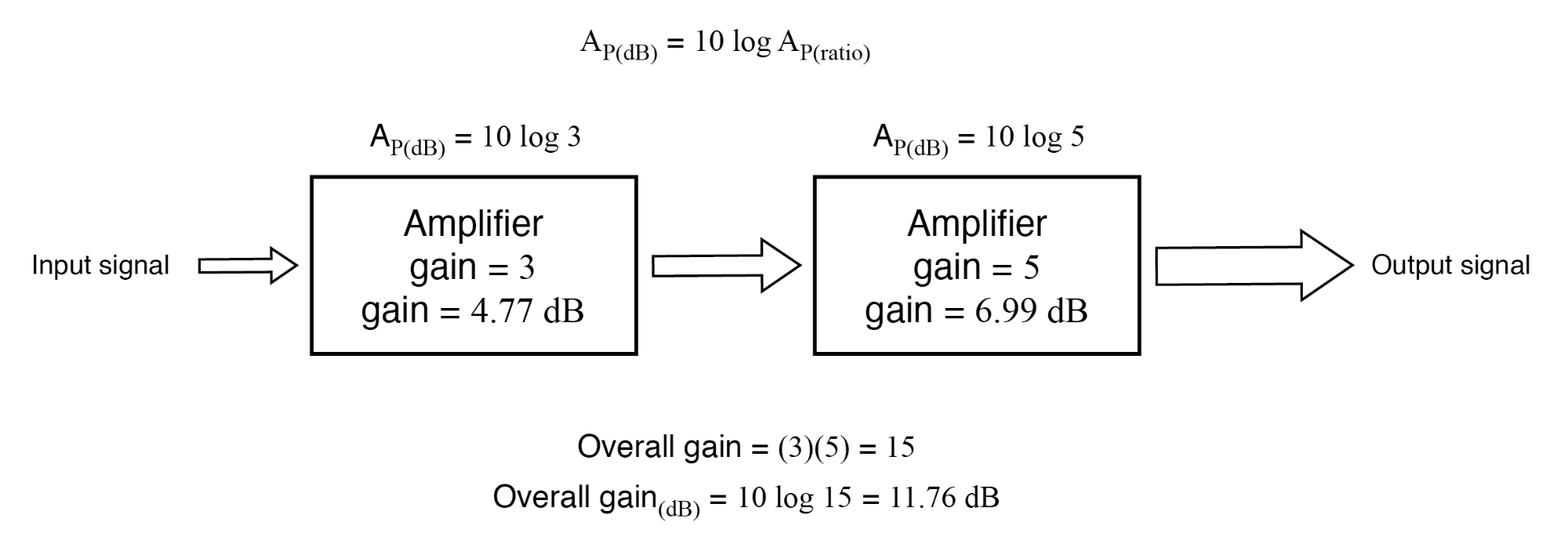
以分贝为单位的放大器级增益是相加的：4.77 dB + 6.99 dB =11.76 dB。

对于那些已经熟悉对数的算术性质的人来说，这并不奇怪。两个数的对数值之和的反对数等于两个原数的乘积，这是代数的基本规则。换句话说，如果我们取两个数字并确定每个数字的对数，然后将这两个对数数字相加，然后确定该和的“反对数”（将对数的底数——在这种情况下，10——提升到该和的幂），结果将与我们简单地将两个原始数字相乘一样。

这个代数规则构成了一个名为滑动规则的设备的核心 ，一种模拟计算机，除其他外，它可以通过加法来确定数字的乘积和商（将滑动木头、金属或塑料秤上标记的物理长度加在一起）。

给定一个对数表，同样的数学技巧可以用来执行复杂的乘法和除法，只需分别进行加法和减法。随着高速、手持、数字计算器设备的出现，这种优雅的计算技术几乎从流行中消失了。但是，在使用本质上是对数的测量尺度时，了解仍然很重要，例如贝尔（分贝）和里氏尺度。

分贝和无单位比的换算

将功率增益从以贝尔或分贝为单位转换为无单位比率时，使用常用对数的数学反函数：10 的幂，或 反对数 .

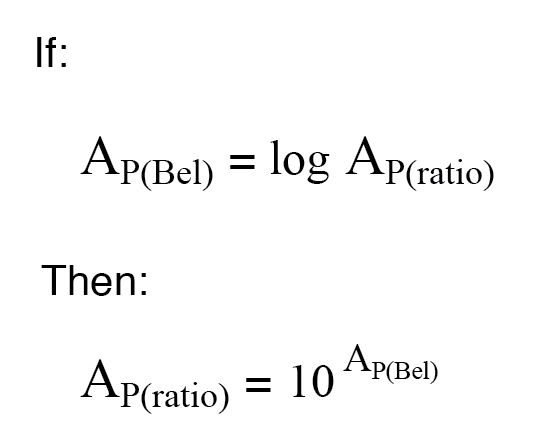
将分贝转换为功率增益的无单位比率大致相同，指数项中仅包含 10 的除法因子：

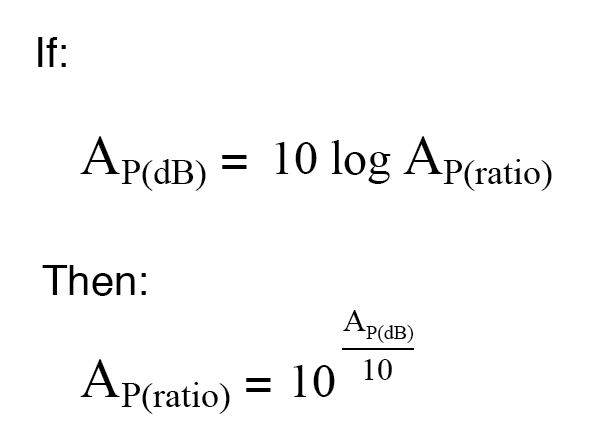
示例： 放大器的功率为 1 瓦，输出功率为 10 瓦。求以 dB 为单位的功率增益。

AP(dB) =10*log10(PO / PI) =10*log10(10 /1) =10*log10(10) =10*(1) =10 dB

示例： 求 20 dB 功率增益的功率增益比 AP(ratio) =(PO / PI)。

AP(dB) =20 =10*log10(APratio) 20/10 =log10*(APratio) 10^(20/10) =10^(log10*(APratio)) 10^2 =100 =AP(ratio) =(PO / PI)

将功率增益转换为电压/电流增益

因为贝尔基本上是功率的单位 系统中的增益或损耗，电压或电流增益和损耗不会以完全相同的方式转换为 bels 或 dB。当使用贝尔或分贝来表示功率以外的增益时，无论是电压还是电流，我们必须根据电压或电流增益量的功率增益来计算。

对于恒定负载阻抗，电压或电流增益为 2 等于功率增益为 4 (2 ² );电压或电流增益为 3 相当于功率增益为 9 (3 ² ）。如果我们将电压或电流乘以给定的系数，那么乘法产生的功率增益将是该系数的平方。这与焦耳定律的形式有关，其中根据电压或电流和电阻计算功率：

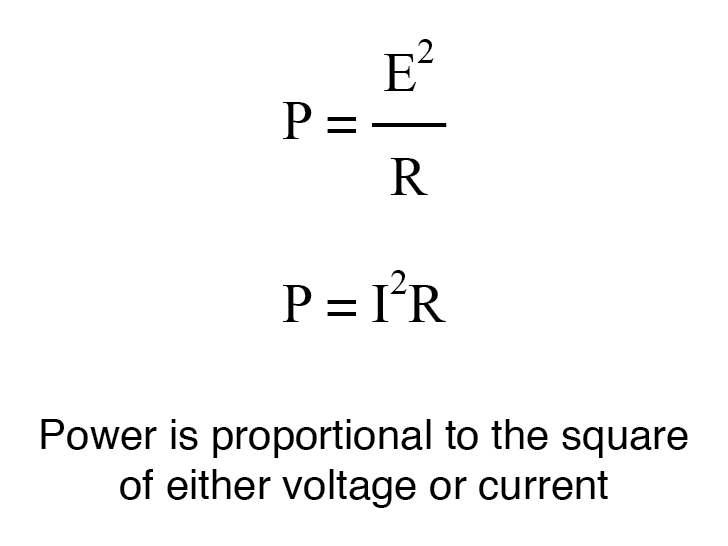
因此，当转换电压或电流增益比率 以 bel 单位表示的相应增益，我们必须在等式中包含这个指数：

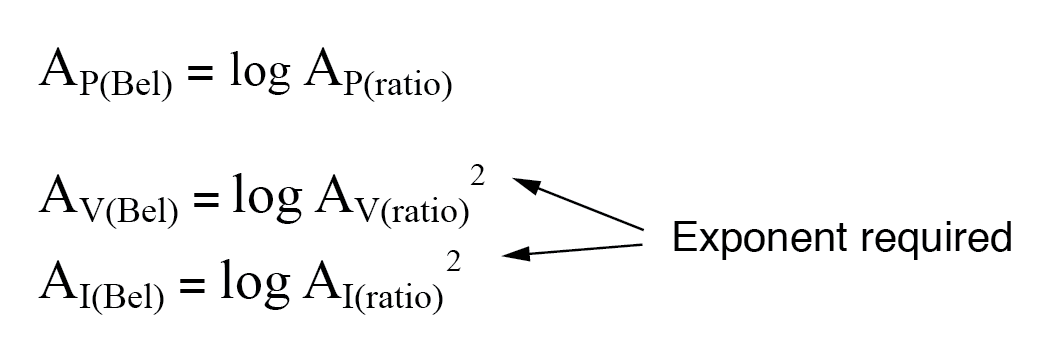
以分贝表示电压或电流增益时，同样的指数要求也适用：

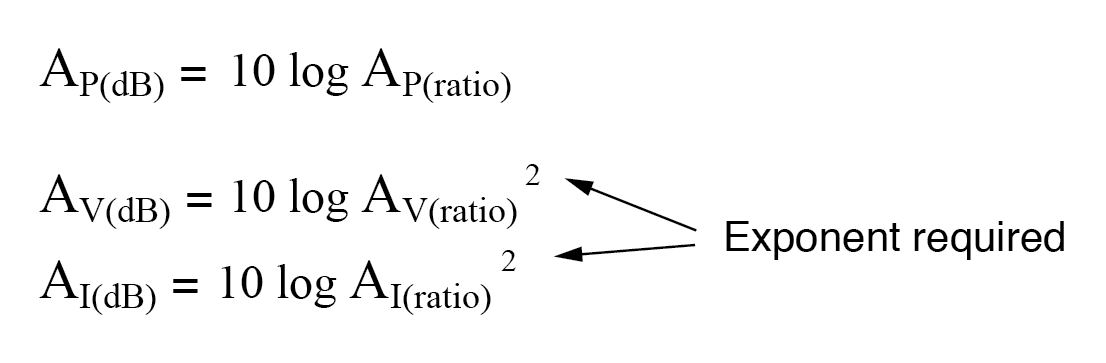
然而，由于对数的另一个有趣特性，我们可以通过将“2”作为乘数来简化这些方程以消除指数 为对数函数。换句话说，而不是取平方的对数 电压或电流增益，我们只需将电压或电流增益的对数乘以2，最终结果以贝尔或分贝为单位：

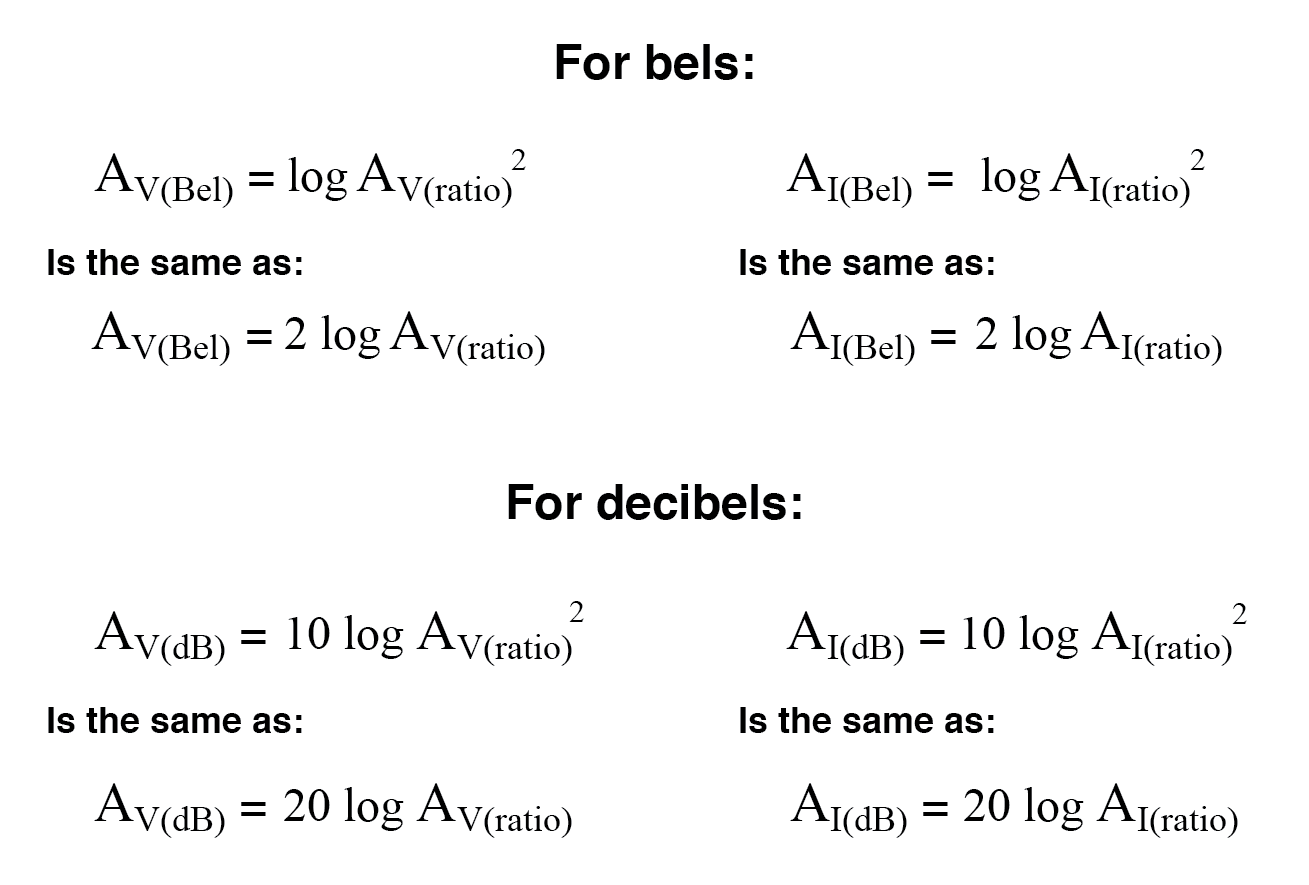
将电压或电流增益从贝尔或分贝转换为无单位比率的过程与功率增益的过程大致相同：

以下是用于将电压或电流增益（以分贝为单位）转换为无单位比率的公式：

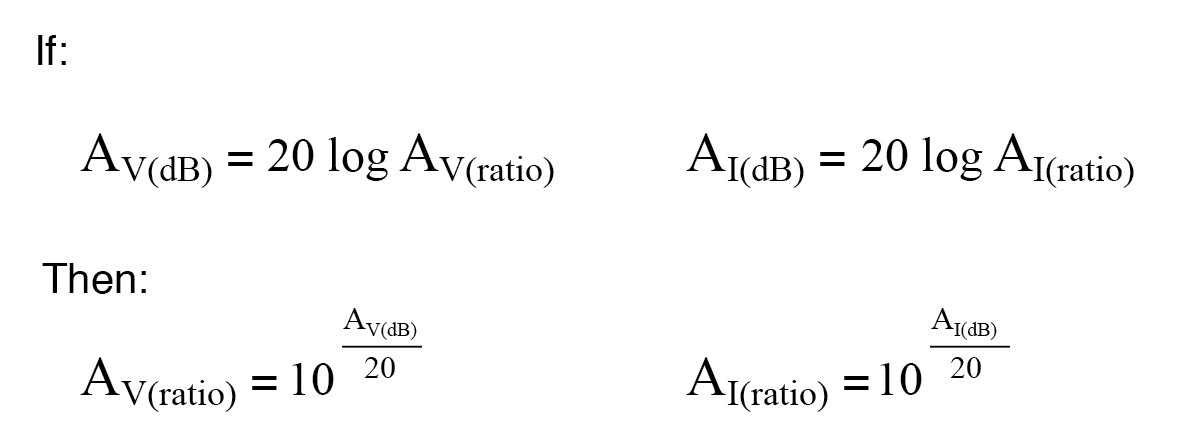
虽然贝尔是一个自然缩放的功率单位，但已经发明了另一种对数单位来直接表示电压或电流增益/损耗，它基于自然 对数而不是常用 贝尔和分贝是对数。被称为 neper ，其单位符号为“Np；但是，可能会遇到小写的“n”。

无论好坏，无论是 neper 还是它的减毒表亲，decineper , 在美国工程应用中常用作单位。 示例： 600 Ω 音频线路放大器的电压为 10 mV，600 Ω 负载两端的电压为 1 V。求功率增益，单位为 dB。

A(dB) =20 log10(VO / VI) =20 log10 (1 /0.01) =20 log10 (100) =20 (2) =40 dB

示例： 求具有 50 Ω 输入和输出阻抗的 20 dB 增益放大器的电压增益比 AV(ratio) =(VO / VI)。

AV(dB) =20 log10 AV(ratio) 20 =20 log10 AV(ratio) 20/20 =log10 AP(ratio) 1020/20 =10log10 (AV(ratio)) 10 =AV(ratio) =( VO / VI)

分贝回顾

• 增益和损耗可以用无单位比率表示，也可以用贝尔 (B) 或分贝 (dB) 单位表示。分贝实际上是 deci -bel：贝尔的十分之一。
• bel 基本上是表达力量的单位 获得或损失。要将功率比转换为贝尔或分贝，请使用以下公式之一：

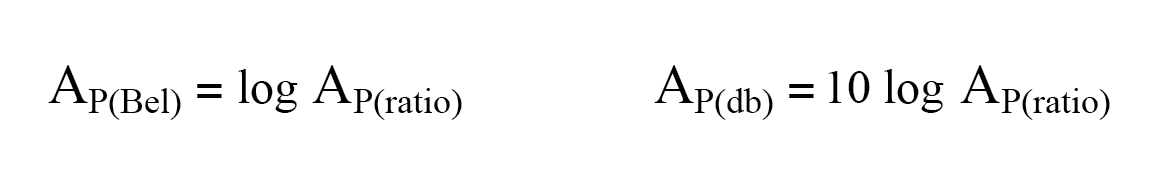
• 当使用贝尔或分贝单位来表示电压 或当前 比率，它必须根据等效的功率进行转换 比率。实际上，这意味着使用不同的方程，对数值的乘法因子为 2，对应于电压或电流增益比的指数 2：

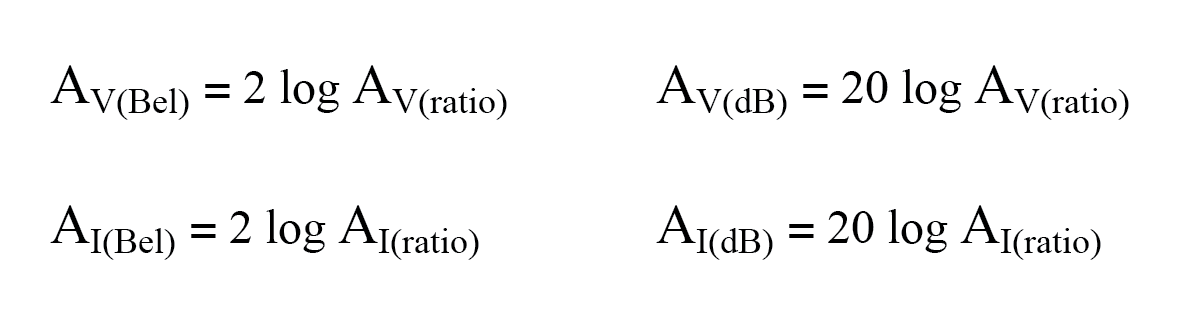
• 要将分贝增益转换为无单位比率增益，请使用以下等式之一：

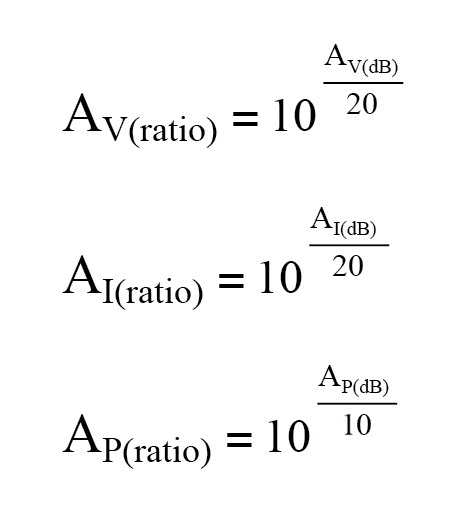
• 增益（放大）表示为正贝尔或分贝数字。损失（衰减）表示为负贝尔或分贝数字。单位增益（无增益或损耗；比率 =1）表示为零贝尔或零分贝。
• 计算由多个放大器级组成的放大器系统的整体增益时，各个增益比相乘 求总增益比。另一方面，每个放大器级的贝尔或分贝数字被添加 共同确定总体收益。

相关工作表：

• 分贝测量工作表
• 基本放大器理论工作表