了解多层感知器的训练公式和反向传播
本文介绍了我们在执行权重更新计算时使用的方程,我们还将讨论反向传播的概念。
欢迎来到 AAC 的机器学习系列。
在这里了解到目前为止的系列:
- 如何使用神经网络进行分类:什么是感知器?
- 如何使用简单的感知器神经网络示例对数据进行分类
- 如何训练基本的感知器神经网络
- 了解简单的神经网络训练
- 神经网络训练理论简介
- 了解神经网络中的学习率
- 使用多层感知器进行高级机器学习
- Sigmoid 激活函数:多层感知器神经网络中的激活
- 如何训练多层感知器神经网络
- 了解多层感知器的训练公式和反向传播
- Python 实现的神经网络架构
- 如何在 Python 中创建多层感知器神经网络
- 使用神经网络进行信号处理:神经网络设计中的验证
- 训练神经网络数据集:如何训练和验证 Python 神经网络
我们已经到了需要仔细考虑神经网络理论中的一个基本主题的地步:计算过程允许我们微调多层感知器 (MLP) 的权重,以便它可以准确地对输入样本进行分类。这会将我们引向“反向传播”的概念,这是神经网络设计的一个重要方面。
更新权重
围绕 MLP 训练的信息很复杂。更糟糕的是,在线资源使用不同的术语和符号,甚至似乎得出不同的结果。但是,我不确定结果是否真的不同,或者只是以不同的方式呈现相同的信息。
本文中包含的方程基于 Dustin Stansbury 博士在此博客文章中提供的推导和解释。他的处理方法是我发现的最好的,如果您想深入研究梯度下降和反向传播的数学和概念细节,这是一个很好的起点。
下图表示我们将在软件中实现的架构,下面的等式对应于该架构,下一篇文章将对此进行更深入的讨论。

术语
如果我们不保持清晰的术语,这个话题很快就会变得难以管理。我将使用以下术语:
- 预激活 (缩写\(S_{preA}\) ):这是指作为节点激活函数输入的信号(实际上只是一次训练迭代上下文中的一个数字)。它是通过执行点积来计算的 包含权重的数组和包含源自前一层节点的值的数组。点积相当于对两个数组执行逐元素乘法,然后对乘法产生的数组中的元素求和。
- 激活后 (缩写\(S_{postA}\) ):这是指退出节点的信号(同样,只是单个迭代上下文中的一个数字)。它是通过将激活函数应用于预激活信号而产生的。我对激活函数的首选术语,表示为 \(f_{A}()\) , 是物流 而不是 sigmoid。
- 在 Python 代码中,您将看到标有 ItoH 的权重矩阵 和 HtoO .我使用这些标识符是因为像“隐藏层权重”这样的说法是模棱两可的——这些会是之前应用的权重 隐藏层或之后 隐藏层?在我的方案中,ItoH 指定应用于从输入节点传输到隐藏节点的值的权重,而 HtoO 指定应用于从隐藏节点传输到输出节点的值的权重。
- 训练样本的正确输出值称为目标 用 T 表示 .
- 学习率 缩写为 LR .
- 最终错误 是来自输出节点的激活后信号之间的差异 (\(S_{postA,O}\) ) 和目标,计算为 \(FE =S_{postA,O} - T\) .
- 错误信号 (\(S_{错误}\) ) 是通过输出节点的激活函数传播回隐藏层的最终误差。
- 渐变 表示给定权重对误差信号的贡献。我们通过减去这个贡献来修改权重(必要时乘以学习率)。
下图将其中一些术语置于网络的可视化配置中。我知道——它看起来像是一团糟。我道歉。这是一个信息密集的图表,虽然乍一看可能有点冒犯,但如果你仔细研究它,我认为你会发现它很有帮助。
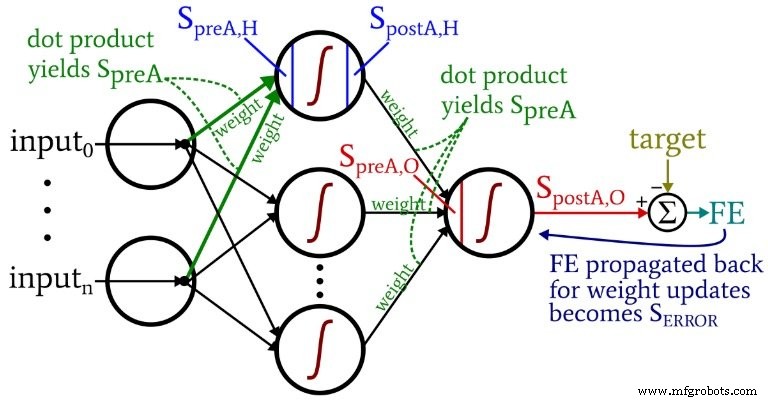
权重更新方程是通过对要修改的权重取误差函数的偏导数推导出来的(我们使用的是平方和误差,请参阅本系列的第 8 部分,它涉及激活函数)。如果你想看数学,请参考斯坦斯伯里博士的帖子;在本文中,我们将直接跳到结果。对于隐藏到输出的权重,我们有以下内容:
\[S_{ERROR} =FE \times {f_A}'(S_{preA,O})\]
\[gradient_{HtoO}=S_{ERROR}\times S_{postA,H}\]
\[weight_{HtoO} =weight_{HtoO}- (LR \times gradient_{HtoO})\]
我们计算错误信号 l 乘以最终误差 通过应用导数时产生的值 激活函数 预激活信号 传递到输出节点(注意素数符号,表示一阶导数,在 \({f_A}'(S_{preA,O})\))。 渐变 然后通过乘以误差信号来计算 通过激活后信号 从隐藏层。最后,我们通过减去这个梯度来更新权重 从当前权重值,我们可以乘以梯度 通过学习率 如果我们想改变步长。
对于输入到隐藏的权重,我们有:
\[gradient_{ItoH} =FE \times {f_A}'(S_{preA,O})\times weight_{HtoO} \times {f_A}'(S_{preA ,H}) \times input\]
\[\Rightarrow gradient_{ItoH} =S_{ERROR} \times weight_{HtoO} \times {f_A}'(S_{preA,H})\times input\]
\[weight_{ItoH} =weight_{ItoH} - (LR \times gradient_{ItoH})\]
使用输入到隐藏的权重,误差必须通过附加层传播回来,我们通过乘以误差信号 通过隐藏到输出权重 连接到感兴趣的隐藏节点。因此,如果我们更新输入到隐藏的权重 导致第一个隐藏节点,我们乘以误差信号 通过将第一个隐藏节点连接到输出节点的权重。然后我们通过执行类似于隐藏到输出权重更新的乘法来完成计算:我们应用导数 激活函数 到隐藏节点的预激活信号 ,“输入”值可以被认为是激活后信号 来自输入节点。
反向传播
上面的解释已经涉及到反向传播的概念。我只是想简要地强调一下这个概念,并确保您对这个术语有明确的熟悉,这个术语经常出现在神经网络的讨论中。
反向传播使我们能够克服第 8 部分中讨论的隐藏节点困境。 我们需要根据网络生成的输出和训练数据提供的目标输出值之间的差异更新输入到隐藏的权重,但这些权重会影响间接生成的输出。
反向传播指的是我们将误差信号发送回一个或多个隐藏层并使用来自隐藏节点的权重和隐藏节点激活函数的导数来缩放该误差信号的技术。整个过程用作根据权重对输出误差的贡献来更新权重的一种方式,即使该贡献被输入到隐藏权重与生成的输出值之间的间接关系所掩盖。
结论
我们已经涵盖了很多重要的材料。我认为我们在本文中有一些关于神经网络训练的非常有价值的信息,我希望你同意。该系列将开始变得更加精彩,所以请回来查看新的分期付款。
工业机器人


