如何训练多层感知器神经网络

我们可以通过添加一层隐藏节点来极大地增强感知器的性能，但这些隐藏节点也使训练变得更加复杂。

到目前为止，在关于神经网络的 AAC 系列中，您已经了解了使用神经网络进行数据分类，尤其是感知器种类。

赶上下面的系列或深入了解这个新条目，它将解释多层感知器 (MLP) 神经网络的基础知识。

上一篇文章表明，单层感知器根本无法产生我们对现代神经网络架构所期望的那种性能。仅限于线性可分函数的系统将无法近似出现在现实生活信号处理场景中的复杂输入-输出关系。解决方案是多层感知器（MLP），比如这个：

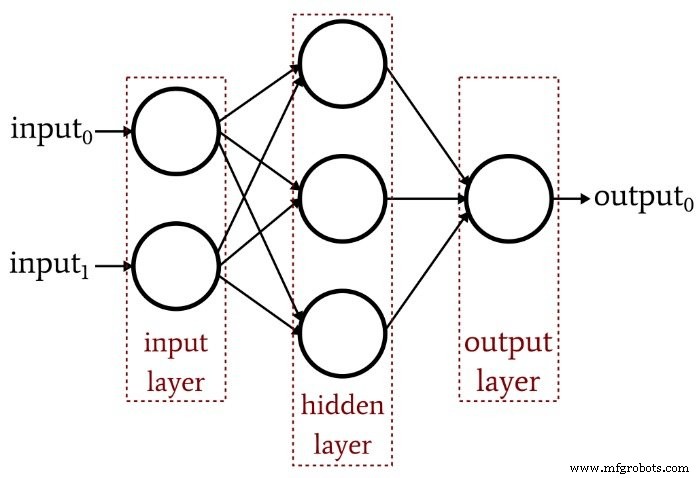
通过添加隐藏层，我们将网络变成了一个“通用逼近器”，可以实现极其复杂的分类。但我们始终要记住，神经网络的价值完全取决于其训练质量。没有丰富多样的训练数据和有效的训练程序，网络永远不会“学习”如何对输入样本进行分类。

让我们看看我们在上一篇文章中用来训练单层感知器的学习规则：

\[w_{new} =w+(\alpha\times(output_{expected}-output_{calculated})\times input)\]

注意这个等式中的隐含假设：我们根据观察到的输出更新权重，因此要使其起作用，单层感知器中的权重必须直接影响输出值。这就像通过旋转冷热两个旋钮来选择水龙头的水温。整体温度和旋钮动作之间的关系相当简单，即使不喜欢数学的人也可以通过摆弄旋钮一段时间来找到所需的水温。

但是现在想象一下，通过冷热管的水流以一种复杂的、高度非线性的方式与旋钮位置相关。您稳定而缓慢地转动热水旋钮，但由此产生的流量变化不规律。你试试冷水的旋钮，它做同样的事情。在这些条件下确定理想的水温——特别是因为“输出”必须通过两种令人困惑的控制关系的组合来实现——会困难得多。

这就是我理解隐藏层困境的方式。将输入节点连接到隐藏节点的权重在概念上类似于那些机械不稳定的旋钮——因为输入到隐藏的权重没有到输出层的直接路径，这些权重与网络输出之间的关系是如此复杂到上面显示的简单学习规则将无效。

由于原始感知器学习规则不能应用于多层网络，我们需要重新考虑我们的训练策略。我们要做的是结合梯度下降和误差函数的最小化。

要记住的一件事是，此训练过程并非特定于多层神经网络。梯度下降来自一般优化理论，我们用于 MLP 的训练过程也适用于单层网络。然而，据我所知，对于单层感知器来说，MLP 风格的梯度下降（至少在理论上）是不必要的，因为上面显示的更简单的规则最终会完成工作。

推导出 MLP 的实际权重更新方程涉及一些令人生畏的数学，我不会在此时尝试智能解释。在本文的其余部分，我的目标是对 MLP 训练的两个关键方面——梯度下降和误差函数——进行概念性介绍，然后我们将在下一篇文章中通过引入新的激活函数来继续讨论。

顾名思义，梯度下降是一种基于斜率下降到误差函数最小值的方法。下图传达了梯度为我们提供有关如何修改权重的信息的方式——误差函数上一个点的斜率告诉我们我们需要去哪个方向以及我们离最小值有多远。

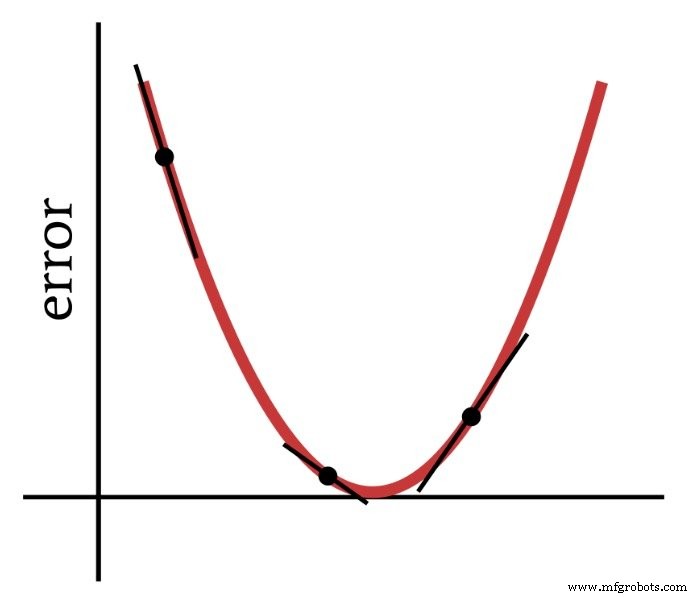
因此，误差函数的导数是我们用来训练多层感知器的计算的重要元素。实际上，我们需要部分衍生品在这里。当我们实施梯度下降时，我们使每个权重修改与误差函数相对于被修改权重的斜率成正比。

量化神经网络误差的常用方法是对每个输出节点的预期（或“目标”）值与计算值之间的差进行平方，然后对所有这些平方差求和。您可以将其称为“平方差之和”或“误差平方和”或其他各种名称，您还会看到缩写 LMS，它代表最小均方，因为训练的目标是最小化均值平方误差。这个误差函数（用E表示）可以用数学表示如下：

\[E=\frac{1}{2}\sum_k(t_k-o_k)^2\]

其中k为输出节点范围，t为目标输出值，o为计算输出值。

我们已经为成功训练多层感知器奠定了基础，我们将在下一篇文章中继续探索这个有趣的话题。

工业机器人