Python 实现的神经网络架构
本文讨论了我们将用于神经网络训练和分类实验的感知器配置,我们还将查看相关主题偏置节点。
欢迎阅读 All About Circuits 神经网络系列技术文章。在迄今为止的系列中(链接如下),我们已经介绍了很多有关神经网络的理论。
- 如何使用神经网络进行分类:什么是感知器?
- 如何使用简单的感知器神经网络示例对数据进行分类
- 如何训练基本的感知器神经网络
- 了解简单的神经网络训练
- 神经网络训练理论简介
- 了解神经网络中的学习率
- 使用多层感知器进行高级机器学习
- Sigmoid 激活函数:多层感知器神经网络中的激活
- 如何训练多层感知器神经网络
- 了解多层感知器的训练公式和反向传播
- Python 实现的神经网络架构
- 如何在 Python 中创建多层感知器神经网络
- 使用神经网络进行信号处理:神经网络设计中的验证
- 训练神经网络数据集:如何训练和验证 Python 神经网络
现在我们准备开始将这些理论知识转化为功能性感知器分类系统。
首先我想介绍一下我们将用高级编程语言实现的网络的一般特征;我使用的是 Python,但代码的编写方式将有助于翻译成 C 等其他语言。下一篇文章提供 Python 代码的详细演练,之后我们将探索不同的训练方式、使用和评估此网络。
Python 神经网络架构
软件对应下图所示的感知器。
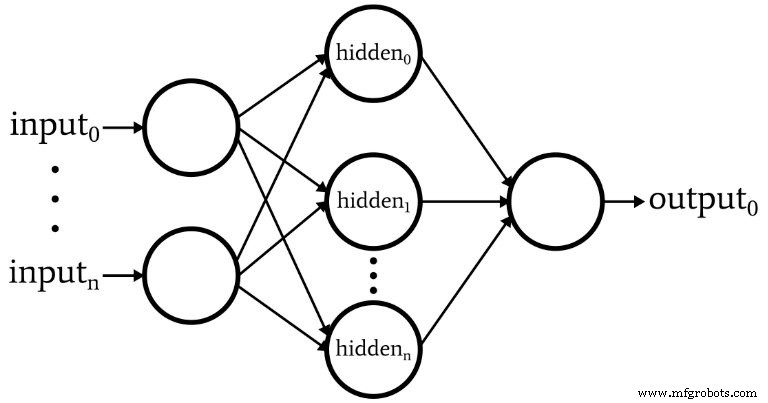
以下是网络的基本特征:
- 输入节点的数量是可变的。如果我们想要一个具有任何显着灵活性的网络,这是必不可少的,因为输入维度必须与我们要分类的样本的维度相匹配。
- 代码不支持多个隐藏层。此时不需要 - 一个隐藏层就足以进行极其强大的分类。
- 一个隐藏层内的节点数量是可变的。寻找隐藏节点的最佳数量涉及一些反复试验,尽管有一些指导方针可以帮助我们选择一个合理的起点。我们将在以后的文章中探讨隐藏层维度的问题。
- 输出节点的数量目前固定为 1。此限制将使我们的初始程序更简单一些,我们可以将可变输出维度合并到改进版本中。
- 隐藏节点和输出节点的激活函数将是标准的逻辑 sigmoid 关系:
\[f(x)=\frac{1}{1+e^{-x}}\]
什么是偏置节点? (如果你是一个感知器,AKA 偏差是好的)
在我们讨论网络架构时,我应该指出,神经网络通常包含称为偏差节点的东西(或者您可以将其称为“偏差”,而没有“节点”)。与偏置节点相关的数值是设计者选择的常数。例如:
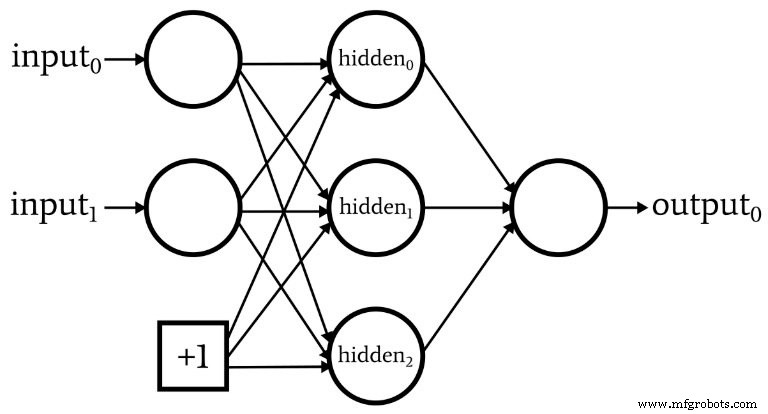
偏置节点可以合并到输入层或隐藏层,或两者兼而有之。它们的权重与任何其他权重一样,并使用相同的反向传播程序进行更新。
使用偏置节点是编写神经网络代码的一个重要原因,它允许您轻松更改输入节点或隐藏节点的数量——即使您只对一个特定的分类任务、可变输入和隐藏层维度感兴趣确保您可以方便地尝试使用偏置节点。
在第 10 部分中,我指出节点的预激活信号是通过执行点积来计算的——即,您将两个数组(或向量,如果您愿意)的相应元素相乘,然后将所有单独的乘积相加。第一个数组保存来自前一层的激活后值,第二个数组保存将前一层连接到当前层的权重。因此,如果前一层激活后数组用x表示,权重向量用w表示,则预激活值计算如下:
\[S_{preA} =w \cdot x =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)\]
您可能想知道这到底与偏置节点有什么关系。好吧,偏差(由 b 表示)修改了这个过程如下:
\[S_{preA} =( w \cdot x)+b =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)+b\]
偏置会改变激活函数处理的信号,从而使网络更加灵活和健壮。使用字母 b 来表示偏差值让人联想到标准直线方程中的“y 截距”:y =mx + b .这绝非偶然的巧合。偏差确实就像一个 y 截距,你可能也注意到了权重数组相当于一个斜率:
\[S_{preA} =( w \cdot x)+b\]
\[y =mx + b\]
权重、偏差和激活
如果我们考虑在训练期间传递给节点激活函数的数值,权重会增加或减少输入数据的斜率,并且偏差会垂直移动输入数据。但这如何影响节点的输出?好吧,让我们假设我们使用标准逻辑函数进行激活:
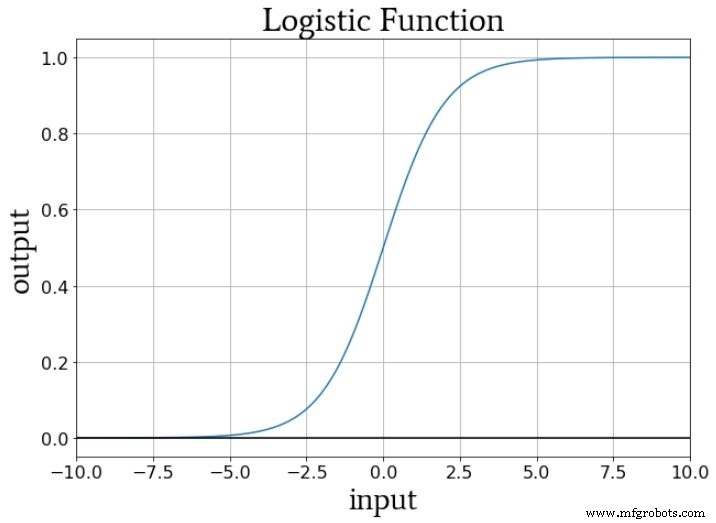
从 fA(x) =0 到 fA(x) =1 的转换以 x =0 的输入值为中心。因此,通过使用偏置来增加或减少预激活信号,我们可以影响转换的发生和从而将激活函数向左或向右移动。另一方面,权重决定输入值如何“快速”通过 x =0,这会影响激活函数中转换的陡度。
结论
我们已经讨论了偏置节点和我们将在软件中实现的第一个神经网络的显着特征。现在我们已准备好查看实际代码,这正是我们在下一篇文章中要做的。
工业机器人


