什么是量子计算以及它是如何工作的?
谷歌、IBM、亚马逊和微软等科技巨头正在将资源投入到量子计算中。量子计算的目标是创造下一代计算机,突破经典计算极限。
尽管取得了进展,但这个新兴领域仍然存在未知领域。
本文介绍了量子计算的基本概念。您将了解什么是量子计算及其工作原理 ,以及将量子设备与标准机器区分开来的原因。
什么是量子计算?定义
量子计算是基于量子力学的新一代计算机,是研究原子和亚原子粒子的物理分支。这些超级计算机以普通计算机无法处理的速度和水平执行计算。
这些是量子设备和普通桌面的主要区别:
- 不同的架构: 量子计算机具有与传统设备不同的架构。例如,使用不同的技术平台(例如超导电路和捕获的原子离子)代替传统的基于硅的存储器或处理器。
- 计算密集型用例: 普通用户可能对量子计算机没有太多用处。这些机器的计算重点和复杂性使其在可预见的未来适用于企业和科学环境。
与标准计算机不同,它的量子对应物可以同时执行多个操作。这些机器还可以在每单位数据中存储更多状态,并运行更高效的算法。
令人难以置信的处理能力使量子计算机能够解决复杂的任务并搜索未分类的数据。
量子计算有什么用?行业用例
采用更强大的计算机使每个行业受益。然而,一些领域已经成为量子计算机取得成功的绝佳机会:
- 医疗保健: 量子计算机有助于以更快的速度开发新药。 DNA 研究也从使用量子计算中受益匪浅。
- 网络安全: 量子编程可以推进数据加密。例如,新的量子密钥分发 (QKD) 系统使用光信号来检测网络攻击或网络入侵者。
- 财务: 公司可以使用量子计算机优化他们的投资组合。欺诈检测和模拟系统也可能会有所改进。
- 交通: 量子计算机可以推动交通规划系统和路线优化方面的进步。
什么是量子比特?
量子计算机强大的关键在于它能够创建和操纵量子比特或量子比特。
这是一个量子比特q0的状态:
q0 = a|0> + b|1>, where a2 + b2 = 1
测量时 q0 为 0 的可能性是 a 2 .测量时为1的概率为b 2 .由于概率性质,一个量子比特可以同时为 0 和 1。
对于 a =1 且 b =0 的量子比特 q0,q0 相当于经典比特 0。测量时有 100% 的机会达到 0 的值。如果 a =0 且 b =1,则 q0 等价于经典比特 1。因此,经典二进制比特 0 和 1 是量子比特的子集。
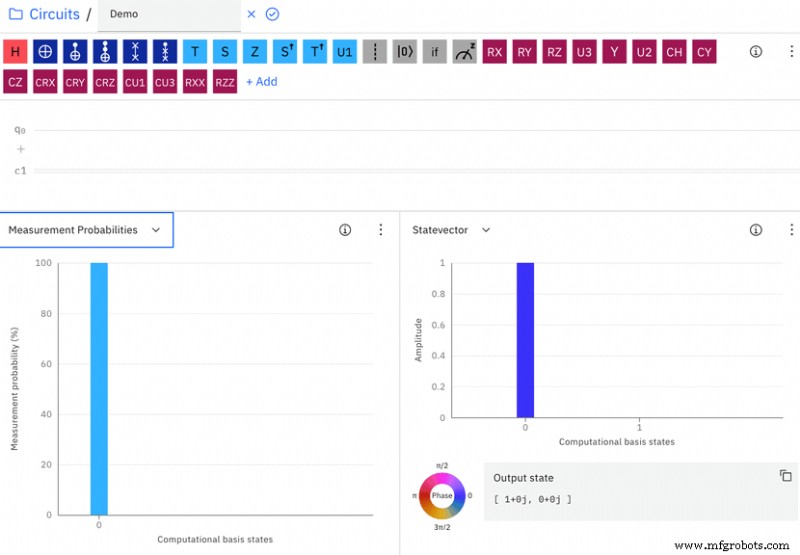
现在,让我们看一下 IBM Circuit Composer 中的一个空电路,其中包含一个 qubit q0(图 1)。 “测量概率”图显示 q0 有 100% 被测量为 0。“状态向量”图显示了 a 和 b 的值,它们分别对应于 0 和 1 “计算基础状态”列。
在图 1 的情况下,a 等于 1,b 等于 0。因此,q0 的概率为 1 2 =1 被测量为 0。
一组连接的量子位比相同数量的二进制位提供更多的处理能力。处理上的差异是由于两个量子特性:叠加 和纠缠 .
量子计算中的叠加
当 0 2 定义 和 b 2 .
Hadamard Gate 是量子计算中的基本门。 Hadamard Gate 将量子比特从 0 或 1 的非叠加状态移动到叠加状态。在叠加状态下,有 0.5 的概率被测量为 0。量子比特也有 0.5 的概率最终为 1。
让我们看看在 q0 上添加 Hadamard Gate(显示为红色 H)的效果,其中 q0 当前处于非叠加状态 0(图 2)。通过 Hadamard 门后,“测量概率”图显示,当测量 q0 时,有 50% 的机会得到 0 或 1。
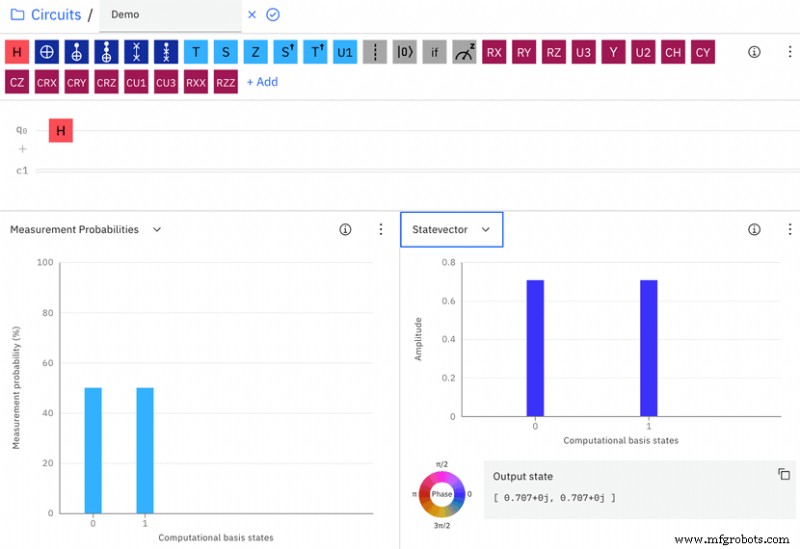
“状态向量”图显示了 a 和 b 的值,它们都是 0.5 =0.707 的平方根。量子比特被测量到 0 和 1 的概率是 0.707 2 =0.5,所以q0现在处于叠加态。
什么是度量?
当我们测量处于叠加态的量子比特时,量子比特会跳到非叠加态。测量会改变量子比特并迫使其脱离叠加状态,进入 0 或 1 状态。
如果一个量子比特处于 0 或 1 的非叠加状态,测量它不会改变任何东西。在这种情况下,量子比特在测量时已经处于 100% 为 0 或 1 的状态。
让我们在电路中添加一个测量操作(图 3)。我们在 Hadamard 门之后测量 q0,并将测量的值输出到 c1 中的位 0(经典位):
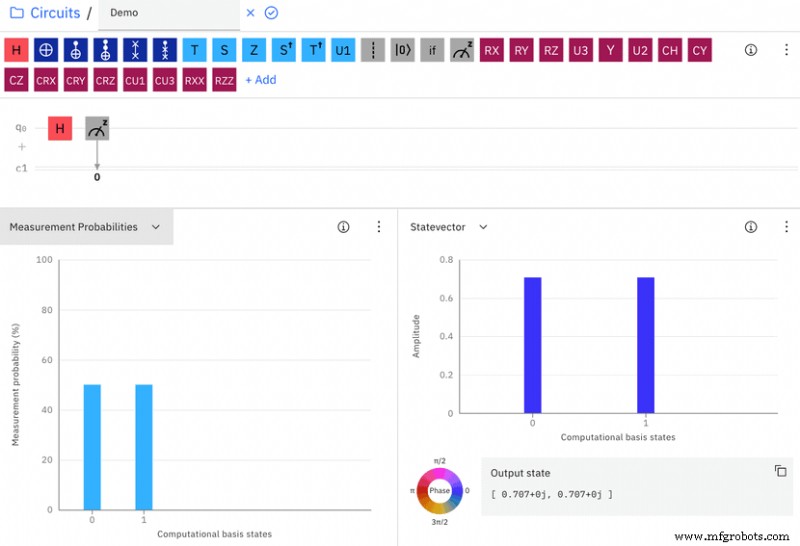
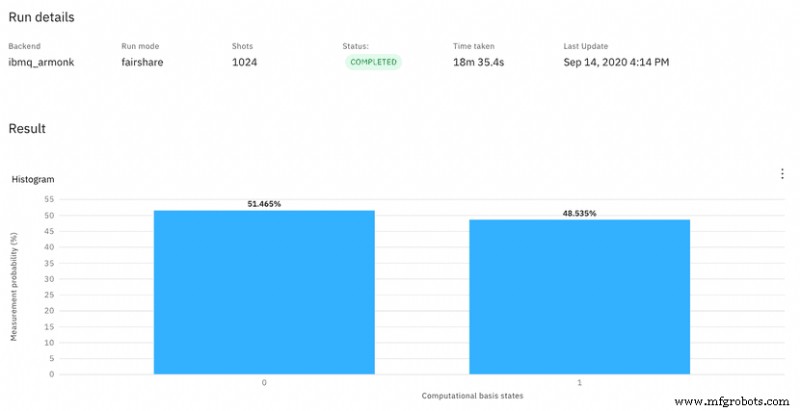
为了查看 Hadamard Gate 之后的 q0 测量结果,我们将电路发送到名为“ibmq_armonk 的实际量子计算机上运行 。”默认情况下,量子电路有 1024 次运行。结果(图4)显示,大约47.4%的时间,q0测量为0。其他52.6%的时间,测量为1:
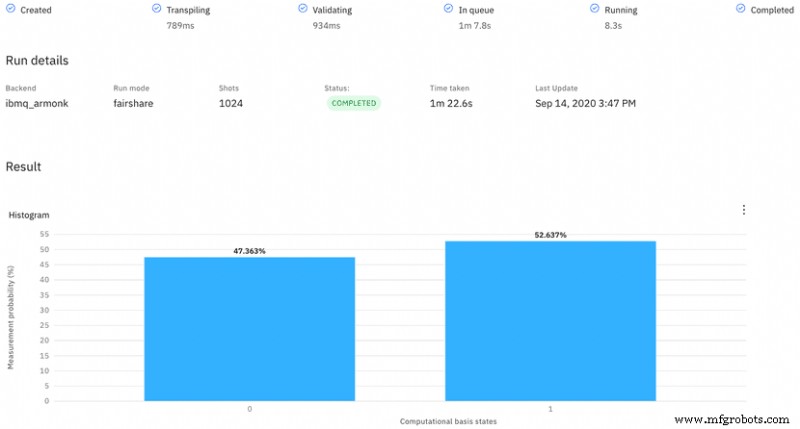
第二次运行(图 5)产生了不同的 0 和 1 分布,但仍接近预期的 50/50 分割:
量子计算中的纠缠
如果两个量子位处于纠缠状态,一个量子位的测量会立即“折叠”另一个量子位的值。即使两个纠缠的量子位相距很远,也会产生同样的效果。
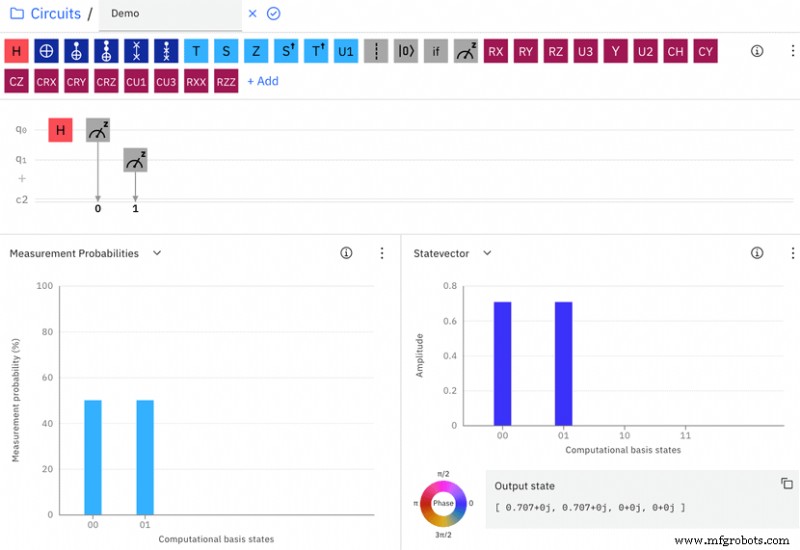
让我们看一个例子。将两个未纠缠的量子位置于纠缠状态的量子操作是 CNOT 门。为了证明这一点,我们首先添加另一个量子位 q1,默认初始化为 0。在 CNOT 门之前,两个量子比特是解开的,因此由于 Hadamard 门,q0 有 0.5 的机会为 0 或 1,而 q1 将是 0。“测量概率”图(图 6)显示概率(q1, q0) 为 (0, 0) 或 (0, 1) 的比例为 50%:
然后我们添加 CNOT 门(显示为蓝点和加号),它将来自 Hadamard 门的 q0 的输出和 q1 作为输入。 “测量概率”图表现在显示,在测量时,(q1, q0) 有 50% 的可能性为 (0, 0),有 50% 的可能性为 (1, 1)(图 7):
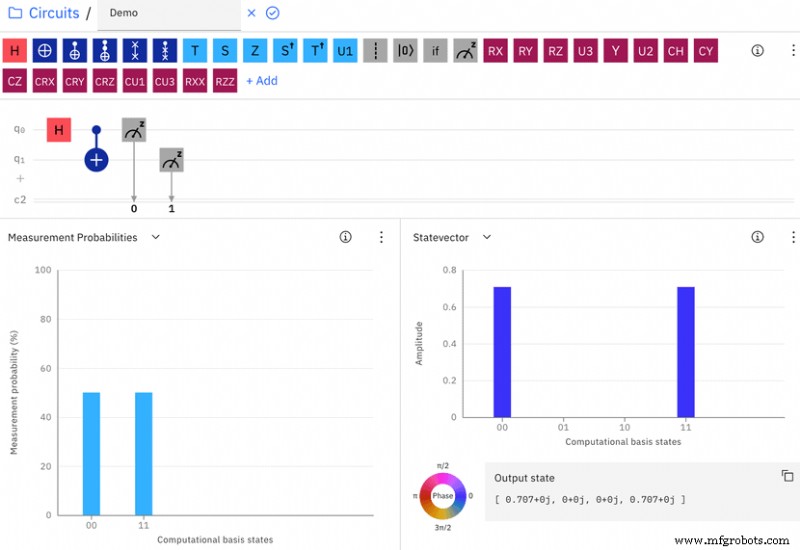
得到 (0, 1) 或 (1, 0) 的机会为零。一旦我们确定了一个量子比特的值,我们就知道另一个量子比特的值,因为两者必须相等。在这种状态下,q0 和 q1 纠缠在一起。
让我们在一台实际的量子计算机上运行它,看看会发生什么(图 8):
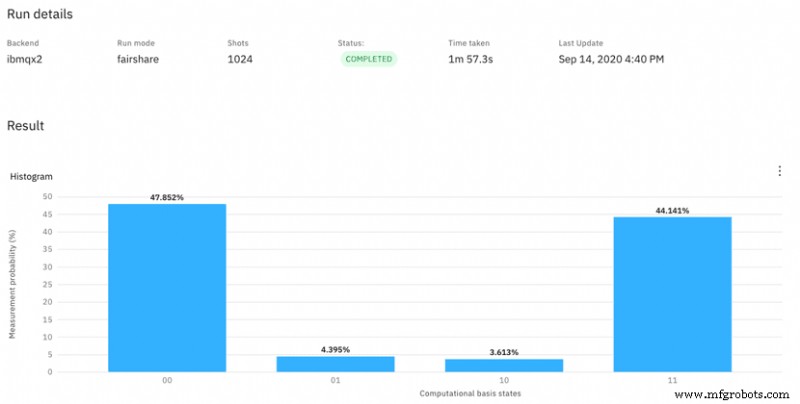
我们接近“00”和“11”状态之间的 50/50 分布。由于量子计算机的高错误率,我们还看到了“01”和“10”的意外出现。虽然经典计算机的错误率几乎不存在,但高错误率是量子计算的主要挑战。
贝尔电路只是一个起点
“纠缠”部分中显示的电路称为贝尔电路。尽管它是基本的,但该电路显示了量子计算的一些基本概念和特性,即量子比特、叠加、纠缠和测量。贝尔电路经常被称为量子计算的 Hello World 程序。
至此,你可能有很多疑问,比如:
- 我们如何在物理上表示一个量子比特的叠加状态?
- 我们如何在物理上测量一个量子位,为什么这会迫使一个量子位变为 0 或 1?
- 量子比特公式中的 |0> 和 |1> 究竟是什么?
- 为什么要 2 和 b 2 对应于一个量子比特被测量为 0 和 1 的机会?
- Hadamard 门和 CNOT 门的数学表示是什么?为什么门将量子比特置于叠加态和纠缠态?
- 我们能解释一下纠缠现象吗?
学习量子计算没有捷径可走。该领域涉及物理、数学和计算机科学等复杂主题。
有大量介绍该技术的好书和视频教程。这些资源通常涵盖线性代数、量子力学和二进制计算等必备概念。
除了书籍和教程之外,您还可以从代码示例中学到很多东西。例如,金融投资组合优化和车辆路线的解决方案是学习量子计算的重要起点。
计算机进化的下一步
量子计算机甚至有可能超越最先进的超级计算机。量子计算可以在科学、医学、机器学习、建筑、交通、金融和紧急服务领域带来突破。
承诺是显而易见的,但该技术仍远未适用于现实生活场景。不过,每天都有新的进展出现,因此预计量子计算将在未来几年造成重大破坏。
云计算


