e
的幂函数的导数
e 的导数示例
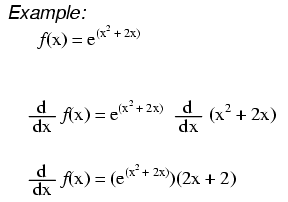
比例常数
当我们说一种关系或现象是“指数的”时,我们是在暗示某些数量——电流、利润、人口——随着数量的增加而增加得更快。换句话说,相对于给定变量的变化率与该变量的值成正比。这意味着指数函数的导数等于原始指数函数乘以一个常数 (k ) 建立相称性。
$$\frac{\text{d}}{\text{d}x}a^x=ka^x$$
比例常数等于指数底的自然对数:
$$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$
因此,如果底的自然对数等于 1,则函数的导数将等于原始函数。这正是 e 的幂函数发生的情况:e 的自然对数是 1,因此 $$e^x$$ 的导数是 $$e^x$$。
$$\frac{\text{d}}{\text{d}x}e^x=e^x$$
“链”规则
当指数表达式不是简单的 x 时,我们应用链式法则:首先取整个表达式的导数,然后乘以指数中表达式的导数。
$$\frac{\text{d}}{\text{d}x}e^{x^2+2x}=e^{x^2+2x}\times\frac{\text{d}}{ \text{d}x}(x^2+2x)=(2x+2)e^{x^2+2x}$$
该技术可用于找到二极管电流相对于二极管电压的变化率。以下等式提供了二极管两端的电压 ($$V_D$$) 与通过二极管的电流 ($$I_D$$) 之间的近似关系:
$$I_D=I_S\times e^\frac{V_D}{0.026}$$
(有关二极管电流-电压方程的更多信息,请参见二极管和整流器页面;另外,请注意 $$I_S$$ 是一个常数,而不是一个变量。)要找到电流相对于电压的变化率,我们取导数:
$$\frac{\text{d}I_D}{\text{d}V_D}=\frac{\text{d}}{\text{d}V_D}(I_S\times e^\frac{V_D}{ 0.026})=I_S\times e^\frac{V_D}{0.026}\times\frac{1}{0.026}$$
因此,在二极管电压 $$V_D$$ 的给定值下,电压的增量增加将产生等于 $$\frac{I_S}{0.026}e^\frac{V_D}{0.026}$$ 的电流增加.
相关工作表:
-
电路微积分练习题
工业技术


