斜率（积分）ADC

到目前为止，我们只能通过使用 DAC 作为 ADC 电路的一部分来避免闪存转换器中组件的庞大数量。然而，这并不是我们唯一的选择。如果我们用一个模拟斜坡电路和一个精确计时的数字计数器代替，就可以避免使用DAC。

这是所谓的single-slope背后的基本思想 ，或集成 ADC。我们不使用具有斜坡输出的 DAC，而是使用称为积分器的运算放大器电路 生成锯齿波，然后通过比较器与模拟输入进行比较。

锯齿波超过输入信号电压电平所需的时间是通过以精确频率方波（通常来自晶体振荡器）计时的数字计数器来测量的。基本原理图如下所示：

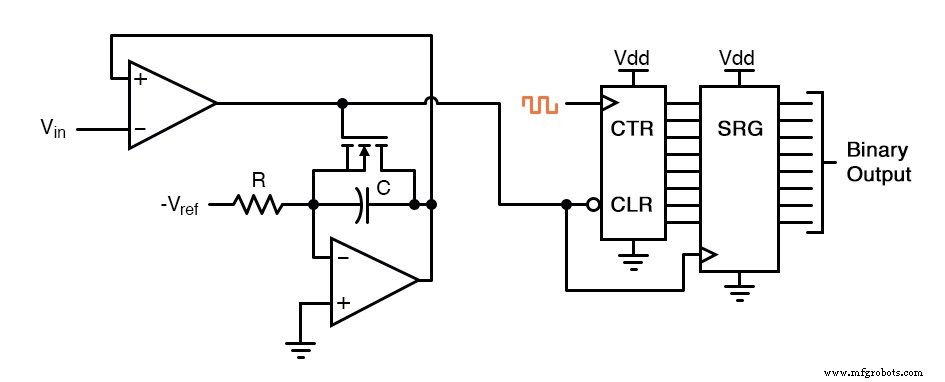
此处显示的 IGFET 电容器放电晶体管方案有点过于简化。实际上，当比较器的输出变高时，很可能必须将一个与时钟信号同步的锁存电路连接到 IGFET 栅极，以确保电容器完全放电。

然而，基本思想在这张图中很明显。当比较器输出低（输入电压大于积分器输出）时，积分器可以以线性方式对电容器充电。同时，计数器以精确时钟频率固定的速率递增计数。

电容器充电到与输入相同的电压电平所需的时间取决于输入信号电平以及 -Vref、R 和 C 的组合。当电容器达到该电压电平时，比较器输出变高，将计数器的输出加载到移位寄存器中作为最终输出。

IGFET 由比较器的高输出触发“开启”，将电容器放电回零伏。当积分器输出电压降至零时，比较器输出切换回低电平状态，清零计数器并使积分器再次升高电压。

此 ADC 电路的行为与数字斜坡 ADC 非常相似，不同之处在于比较器参考电压是平滑的锯齿波而非“阶梯”：

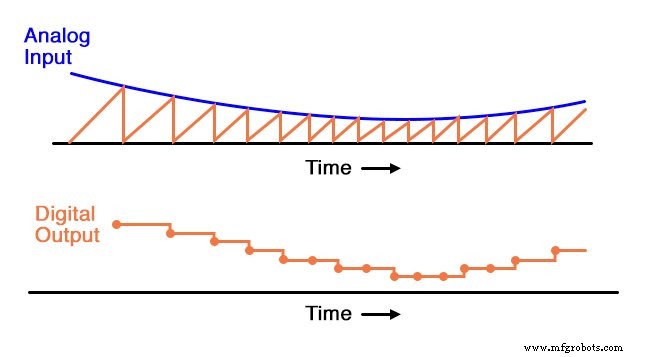
单斜率 ADC 具有数字斜坡 ADC 的所有缺点，另外还有校准漂移 .该 ADC 的输出与其输入的准确对应取决于与计数器的计数率（时钟频率）匹配的积分器的电压斜率。

对于数字斜坡 ADC，时钟频率对转换精度没有影响，只对更新时间有影响。在该电路中，由于积分率和计数率是相互独立的，随着时间的推移，两者之间的变化是不可避免的，会导致精度的损失。

该电路唯一的优点是避免使用DAC，降低了电路复杂度。

双斜率转换器

在称为双斜率的设计变体中可以找到解决这种校准漂移困境的方法 转换器。在双斜率转换器中，积分器电路在交替循环中被正负驱动以斜坡下降然后上升，而不是在每个周期结束时重置为 0 伏。

在斜坡的一个方向上，积分器由正模拟输入信号驱动（产生负的、可变的输出电压变化率，或输出斜率 ) 一段固定的时间，由具有精确频率时钟的计数器测量。然后，在另一个方向，用一个固定的参考电压（产生一个固定的输出电压变化率）随时间由同一个计数器测量。

当积分器的输出达到与开始周期的固定时间部分时相同的电压时，计数器停止计数。积分器的电容器放电回其原始输出电压所需的时间量（由计数器累积的幅度测量）成为 ADC 电路的数字输出。

双斜率方法可以类似于机械时钟机构中使用的旋转弹簧。想象一下，我们正在构建一个机制来测量轴的转速。

因此，轴速度是我们要由该设备测量的“输入信号”。测量周期从处于松弛状态的弹簧开始。

然后弹簧被旋转轴（输入信号）转动或“上紧”一段固定的时间。这会将弹簧置于与轴速度成正比的特定张力中：轴速度越大，上链速度越快，并且在这段时间内积累的弹簧张力越大。

之后，弹簧从轴上脱开并允许以固定速率松开，由计时器装置测量其松开回到松弛状态的时间。 时间 弹簧以固定速率展开所需的时间将与速度成正比 它在周期的固定时间部分缠绕（输入信号幅度）。

这种模数转换技术避免了单斜率 ADC 的校准漂移问题，因为积分器的积分系数（或“增益”）和计数器的速率在整个“卷绕”和“展开”期间都有效”循环部分。如果计数器的时钟速度突然增加，这将缩短积分器“结束”的固定时间段（导致积分器积累的电压较小），但这也意味着它会在此期间计数得更快允许积分器以固定速率“展开”的时间。

计数器计数较快的比例将与时钟速度变化前积分器的累积电压减少的比例相同。因此，时钟速度误差将自行抵消，数字输出将完全正确。

这种方法的另一个重要优点是输入信号在周期的固定时间部分驱动积分器时变得平均。这段时间内模拟信号的任何变化都会对该周期结束时的数字输出产生累积影响。

其他 ADC 策略仅在每个周期的单个时间点“捕获”模拟信号电平。如果模拟信号“有噪声”（包含大量虚假电压尖峰/骤降），其他 ADC 转换器技术之一可能偶尔会转换尖峰或骤降，因为它在单个时间点重复捕获信号。

另一方面，双斜率 ADC 将积分周期内的所有尖峰和下降平均在一起，从而提供具有更高抗噪性的输出。双斜率 ADC 用于要求高精度的应用。

相关工作表：

• 模数转换工作表