节点电压法

节点电压分析方法根据 KCL 方程组求解电路节点处的未知电压。这种分析看起来很奇怪，因为它涉及用等效电流源替换电压源。此外，以欧姆为单位的电阻值被以西门子为单位的等效电导取代，G =1/R。西门子 (S) 是电导的单位，取代了姆欧单位。在任何情况下，S =Ω-1。并且 S =mho（已过时）。

节点电压计算方法

我们从具有传统电压源的电路开始。选择一个公共节点 E0 作为参考点。节点电压E1和E2是针对这一点计算的。

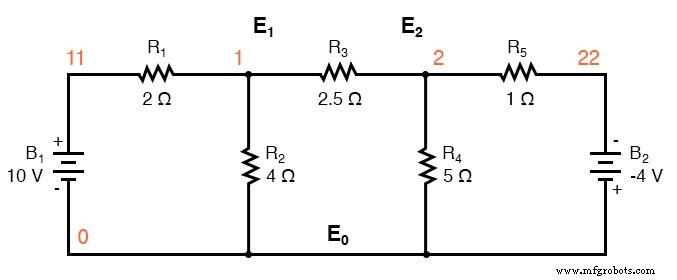
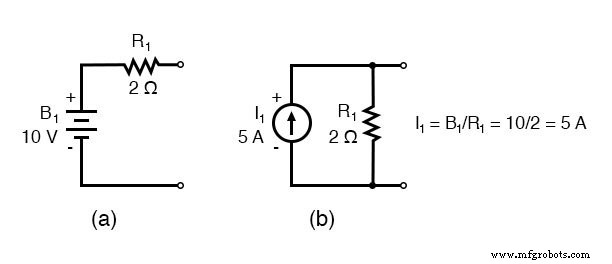
用等效电流源和并联电阻器代替电压源和相关的串联电阻器产生修改后的电路。用电阻用西门子电阻代替欧姆电阻。

<前> I1 =E1/R1 =10/2 =5 A I2 =E2/R5 =4/1 =4 A G1 =1/R1 =1/2 Ω =0.5 S G2 =1/R2 =1/4 Ω =0.25 S G3 =1/R3 =1/2.5 Ω =0.4 S G4 =1/R4 =1/5 Ω =0.2 S G5 =1/R5 =1/1 Ω =1.0 S

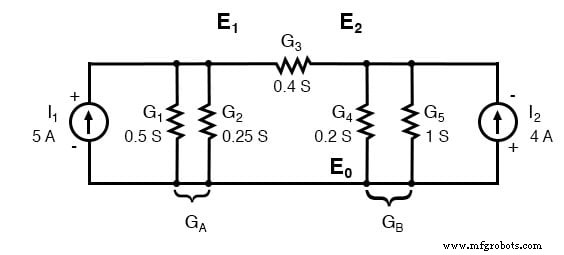
并联电导（电阻器）可以通过增加电导来组合。不过，我们不会重绘电路。该电路已准备好用于节点电压法的应用。

<前> GA =G1 + G2 =0.5 S + 0.25 S =0.75 S GB =G4 + G5 =0.2 S + 1 S =1.2 S

推导出一个通用的节点电压方法，我们一次用未知的节点电压 V1 和 V2 写出一对 KCL 方程。我们这样做是为了说明通过检查编写方程的模式。

<前> GAE1 + G3(E1 - E2) =I1 (1) GBE2 - G3(E1 - E2) =I2 (2) (GA + G3 )E1 -G3E2 =I1 (1) -G3E1 + (GB + G3)E2 =I2 (2)

上面最后一对方程的系数已重新排列以显示模式。连接到第一节点的电导总和是等式（1）中第一电压的正系数。连接到第二节点的电导总和是等式（2）中第二电压的正系数。其他系数为负，代表节点之间的电导。对于这两个方程，右侧等于连接到节点的相应电流源。这种模式使我们能够通过检查快速编写方程式。这就引出了一套分析节点电压方法的规则。

节点电压规则：

• 将与电阻串联的电压源转换为与电阻并联的等效电流源。
• 将电阻值更改为电导。
• 选择一个参考节点(E0)
• 将未知电压 (E1)(E2) ... (EN) 分配给其余节点。
• 为每个节点 1,2, ... N 写一个 KCL 方程。第一个方程中第一个电压的正系数是连接到节点的电导之和。第二个方程中第二个电压的系数是连接到该节点的电导之和。对第三个电压的系数、第三个方程和其他方程重复。这些系数落在对角线上。
• 所有方程的所有其他系数都是负数，表示节点之间的电导。第一个方程，第二个系数是节点1到节点2的电导，第三个系数是节点1到节点3的电导。其他方程填负系数。
• 等式的右侧是连接到各个节点的电流源。
• 求解未知节点电压的方程组。

节点电压法示例

示例： 使用上图中的数值建立方程并求解节点电压。

解决方案：

<前> (0.5+0.25+0.4)E1 -(0.4)E2=5 -(0.4)E1 +(0.4+0.2+1.0)E2 =-4 (1.15)E1 -(0.4)E2=5 -(0.4)E1 +(1.6)E2 =-4 E1 =3.8095 E2 =-1.5476

可以使用计算器或八度音程（未显示）来求解两个方程。该解决方案基于带有电压源的原始原理图通过 SPICE 进行了验证。不过，可以模拟带有电流源的电路。

<前> V1 11 0 直流 10 V2 22 0 直流 -4 r1 11 1 2 r2 1 0 4 r3 1 2 2.5 r4 2 0 5 r5 2 22 1 .DC V1 10 10 1 V2 -4 -4 1 .print DC V(1) V(2) 。结尾 v(1) v(2) 3.809524e+00 -1.547619e+00

再举一个例子。这个有三个节点。我们没有在示意图上列出电导。但是，G1 =1/R1 等

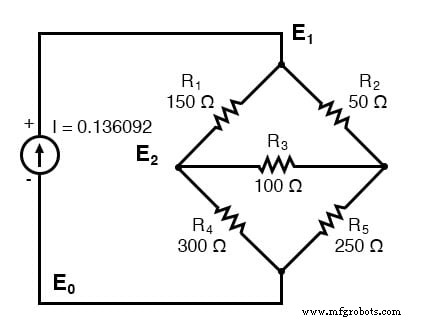
有三个节点可以通过检查来编写方程。请注意，方程 (1) E1、方程 (2) E2 和方程 (3) E3 的系数为正。这些是连接到节点的所有电导的总和。所有其他系数都是负的，代表节点之间的电导。等式的右侧是相关的电流源，节点 1 处唯一的电流源为 0.136092 A。由于缺少电流源，右侧的其他等式为零。我们懒得计算图上电阻的电导。因此，下标 G 是系数。

 (G1 + G2)E1 -G1E2 -G2E3 =0.136092 -G1E1 +(G1 + G3 + G4)E2 -G3E3 =0 -G2E1 -G3E2 +(G2 + G3 + G5)E3 =0 

我们太懒了，我们将倒数电阻和倒数电阻的总和输入到八度“A”矩阵中，让八度计算“A=”之后的电导矩阵。最初的输入行很长，以至于它被分成了三行。这与之前的示例不同。输入的“A”矩阵由开始和结束方括号划定。列元素以空格分隔。行以“新行”分隔。不需要逗号和分号作为分隔符。但是，“b”处的电流向量以分号分隔，以产生电流列向量。

<前> 八度：12> A =[1/150+1/50 -1/150 -1/50> -1/150 1/150+1/100+1/300 -1/100> -1/50 -1/100 1/50+1/100+1/250] 一 =0.0266667 -0.0066667 -0.0200000 -0.0066667 0.0200000 -0.0100000 -0.0200000 -0.0100000 0.0340000 八度：13> b =[0.136092;0;0] 乙 =0.13609 0.00000 0.00000 八度：14> x=A\b x =24.000 17.655 19.310

注意“A”矩阵对角线系数为正，其他所有系数均为负。

作为电压矢量的解位于“x”处。 E1 =24.000 V，E2 =17.655 V，E3 =19.310 V。这三个电压与之前的网状电流和不平衡桥问题的 SPICE 解决方案进行了比较。这并非巧合，因为我们特意选择了 0.13609 A 的电流源，以产生在该问题中用作电压源的 24 V。

总结

• 给定电导和电流源网络，电路分析的节点电压方法可从 KCL 方程求解未知节点电压。
• 有关通过检查编写方程式的详细信息，请参阅上述规则。
• 电导G的单位是西门子S。电导是电阻的倒数：G =1/R

相关工作表：

• 精密二极管电路工作表
• 基尔霍夫定律工作表