电路效果

非正弦重复波形等效于一系列不同频率的正弦波的原理是一般波的基本性质，对交流电路的研究具有重要的实际意义。

这意味着任何时候我们的波形不是完美的正弦波形，所讨论的电路都会做出反应，就好像它同时施加了一系列不同频率的电压一样。

当交流电路承受由多种频率组成的电源电压时，该电路中的组件以不同的方式响应每个组成频率。任何电抗元件（例如电容器或电感器）都会同时对电路中的每个频率呈现独特的阻抗量。

值得庆幸的是，通过应用叠加定理，对此类电路的分析变得相对容易 ，将多频源看作是一组串联的单频电压源，一次分析一个源的电路，最后将结果相加得出总和：

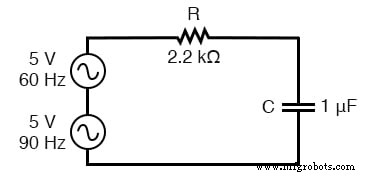
由频率组合驱动的电路：60 Hz 和 90 Hz

单独60Hz源的分析电路：

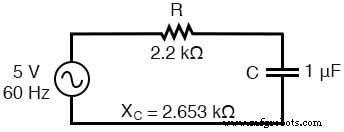
解决 60 Hz 的电路

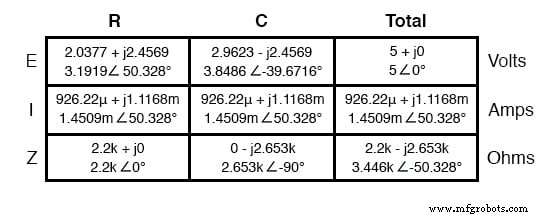
单独分析 90 Hz 源的电路：

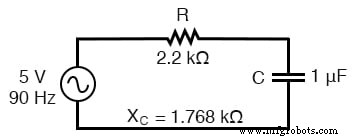
解决 90 Hz 的电路

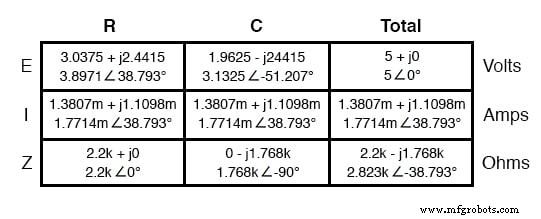
叠加 R 和 C 上的压降，我们得到：

由于每个组件上的两个电压处于不同的频率，我们无法将它们合并为一个单一的电压图，如果我们将相同频率下不同幅度和/或相位角的两个电压加在一起就可以了。

复数符号使我们能够表示波形幅度（极坐标幅度）和相位角（极角），但不能表示频率。

我们可以从叠加定理的这个应用中看出，电容器两端的 60 Hz 电压降比 90 Hz 电压大。电阻的压降正好相反。

这是值得注意的，特别是考虑到两个源电压相等的事实。正是这种对不同频率信号的不均衡电路响应，将是我们下一章的重点。

我们还可以将叠加定理应用于由非正弦电压（例如方波）供电的电路的分析。如果我们知道该波的傅里叶级数（多个正弦/余弦波等效值），我们可以将其视为源自具有适当幅度、频率和相移的多个正弦电压源的串联串。

不用说，这对于某些波形来说可能是一项艰巨的任务（准确的方波傅立叶级数被认为可以表达为九次谐波，或总共五个正弦波！），但这是可能的。我提到这一点不是为了吓唬您，而是要告诉您看似简单的波形背后潜在的复杂性。

实际电路对方波供电的响应与由无限供电的响应相同 一系列奇数倍频率和递减幅度的正弦波。

众所周知，这会转化为意外的电路谐振、变压器和电感器磁芯由于涡流、宽频谱范围内的电磁噪声等而过热。技术人员和工程师需要意识到非正弦波形在电抗电路中的潜在影响。

众所周知，谐波也以电磁辐射的形式表现出来。

已经对在客机上使用便携式计算机的潜在危害进行了研究，理由是计算机的高频方波“时钟”电压信号能够产生无线电波，可能会干扰飞机电子导航设备的运行.

典型的微处理器时钟信号频率在飞机无线电频段的范围内已经够糟糕的了，但更糟糕的是这些基频的谐波倍数跨越更大的范围，因为时钟信号电压是平方-波形而不是正弦波。

这种性质的电磁“辐射”在工业应用中也可能是一个问题，由于电机和电炉功率的（非线性）电子控制，谐波数量非常多。

基本电力线频率可能只有 60 Hz，但这些谐波频率的倍数理论上可以扩展到无限高的频率范围。低频电源线电压和电流不会像电磁能那样很好地辐射到空间，但高频可以。

此外，由近距离导体引起的电容性和电感性“耦合”通常在高频下更为严重。与纯正弦波干扰相比，靠近电源线的信号线更容易从电源线“拾取”谐波干扰。

当旧的电机控制被新的固态电子电机控制取代时，这个问题会在工业中表现出来，以提供更高的能源效率。

突然之间，可能会有奇怪的电噪声被施加到以前从未出现过的信号线上，因为旧的控制装置从未产生谐波，并且这些高频谐波电压和电流倾向于以电感和电容的方式“耦合”到附近的导体，而不是其他任何来自旧控件的 60 Hz 信号曾经使用过。

评论：

• 任何规则（重复）、非正弦波形都等效于一系列不同频率、相位和幅度的特定正弦/余弦波，并在必要时加上直流偏置电压。确定任何波形的正弦波形等效值的数学过程称为傅立叶分析 .
• 通过串联多个单频电压源，可以模拟多频电压源进行分析。电压和电流的分析是通过使用叠加定理来完成的。注意：叠加不同频率的电压和电流不能 以复数形式相加，因为复数只说明幅度和相移，而不是频率！
• 谐波会在附近的电路上施加不需要的（“噪声”）电压信号，从而导致问题。这些不需要的信号可能来自电容耦合、电感耦合、电磁辐射或它们的组合。

相关工作表：

• 叠加定理工作表