网格当前方法和分析

网格电流法 ，也称为环流方法 , 与支路电流方法非常相似，因为它使用联立方程、基尔霍夫电压定律和欧姆定律来确定网络中的未知电流。它与 Branch Current 方法的不同之处在于它不 使用基尔霍夫电流定律，它通常可以解决未知变量较少和联立方程较少的电路，如果你不得不在没有计算器的情况下解决这个问题，这尤其好。

Mesh Current，常规方法

让我们看看这个方法如何处理同一个示例问题：

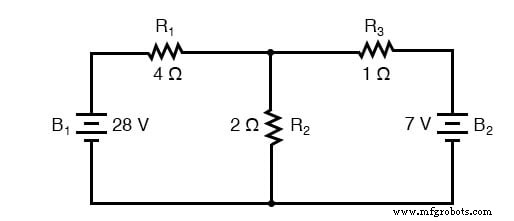
识别循环

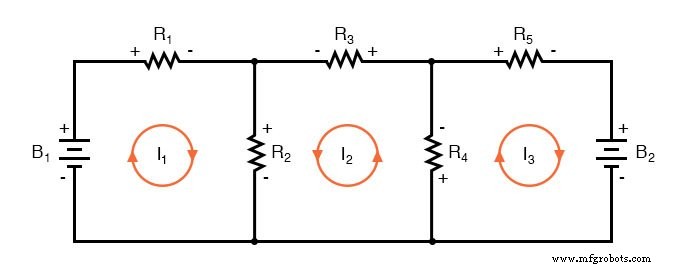
网格电流方法的第一步是识别包含所有组件的电路中的“回路”。在我们的示例电路中，由 B1、R1 和 R2 形成的回路将是第一个，而由 B2、R2 和 R3 形成的回路将是第二个。网格电流方法最奇怪的部分是设想每个回路中的循环电流。事实上，这种方法得名于这些电流在循环之间啮合在一起的想法，就像一组旋转齿轮：

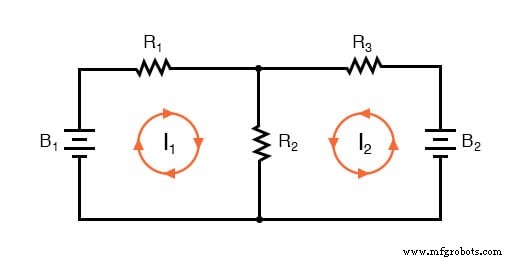
每个电流方向的选择完全是任意的，就像在分支电流方法中一样，但是如果电流通过相交组件流向相同的方向，则结果方程更容易求解（注意电流 I1 和 I2 如何都“上升”通过电阻器 R2，它们在那里“啮合”或相交）。如果网格电流的假定方向错误，则该电流的答案将为负值。

标记压降极性

下一步是根据网状电流的假定方向标记电阻器上的所有电压降极性。请记住，电阻器的“上游”端始终为负，而电阻器的“下游”端相对于彼此为正，因为电子带负电。当然，电池极性由图中的符号方向决定，并且可能与电阻器极性（假设的电流方向）“一致”，也可能不“一致”：

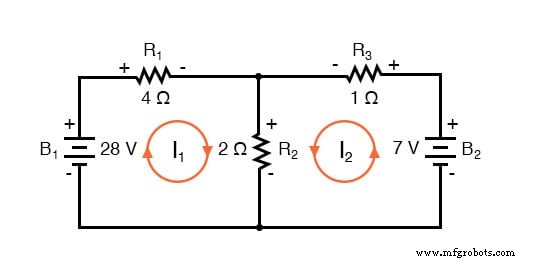
使用基尔霍夫电压定律，我们现在可以绕过这些循环中的每一个，生成代表组件电压降和极性的方程。与分支电流方法一样，我们将电阻的电压降表示为电阻（以欧姆为单位）与其各自的网状电流（此时该量未知）的乘积。当两个电流啮合在一起时，我们将把该项写在等式中，其中电阻器电流是和 两个啮合电流。

用方程追踪电路的左环

追踪电路的左循环，从左上角开始逆时针移动（起点和方向的选择最终无关紧要），像我们手上有一个电压表一样计算极性，前面的点是红色的和黑铅在后面的点，我们得到这个等式：

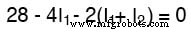
请注意，等式的中间项使用网状电流 I1 和 I2 的总和作为通过电阻器 R2 的电流。这是因为网状电流 I1 和 I2 流经 R2 的方向相同，因此相互补充。将系数 2 分配给 I1 和 I2 项，然后将等式中的 I1 项合并，我们可以简化为：

这时候我们有一个方程有两个未知数。为了能够求解两个未知的网格电流，我们必须有两个方程。如果我们跟踪电路的另一个回路，我们可以获得另一个 KVL 方程，并有足够的数据来求解这两个电流。我是习惯的生物，我将从右循环的左上角开始逆时针追踪：

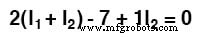
像以前一样简化等式，我们最终得到：

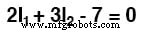
解决未知问题

现在，通过两个方程，我们可以使用几种方法之一来数学求解未知电流 I1 和 I2：

重绘电路

知道这些解决方案是 mesh 的价值 电流，而不是分支 电流，我们必须回到我们的图表，看看它们如何组合在一起以提供通过所有组件的电流：

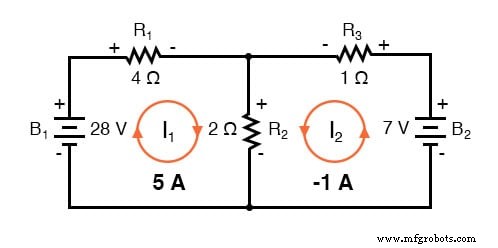
I2 为 -1 amp 的解决方案意味着我们最初假设电流方向不正确。实际上，I2 以（正）1 安培的值沿逆时针方向流动：

由于电流 I2，电流方向从最初假设的变化将改变 R2 和 R3 两端的电压降的极性。从这里，我们可以说通过 R1 的电流为 5 安培，R1 上的压降是电流和电阻的乘积 (E=IR)，20 伏特（左侧为正，右侧为负）。

此外，我们可以肯定地说，通过 R3 的电流为 1 安培，电压降为 1 伏 (E=IR)，左侧为正，右侧为负。但是 R2 发生了什么？

网格电流 I1 通过 R2 “下降”，而网格电流 I2 通过 R2 “上升”。要确定通过 R2 的实际电流，我们必须查看网格电流 I1 和 I2 如何相互作用（在这种情况下它们是对立的），并将它们代数相加以获得最终值。由于 I1 以 5 安培“下降”，而 I2 以 1 安培“上升”，真实 通过 R2 的电流必须为 4 安培，“下降”：

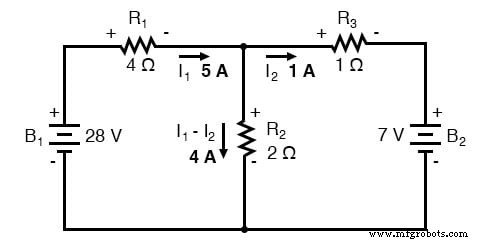
4 安培的电流通过 R2 的 2 Ω 电阻给我们一个 8 伏的电压降 (E=IR)，顶部为正，底部为负。

网格电流分析的优势

网格电流分析的主要优点是它通常允许解决具有较少未知值和较少联立方程的大型网络。我们的示例问题使用三个方程来求解分支电流方法，而使用网格电流方法仅使用两个方程。随着网络复杂性的增加，这种优势会变得更大：

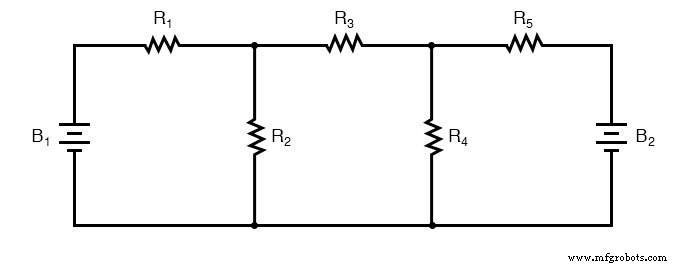
为了使用分支电流解决这个网络，我们必须建立五个变量来解释电路中的每个独特电流（I1 到 I5）。这将需要五个方程来求解，形式为两个 KCL 方程和三个 KVL 方程（节点处 KCL 的两个方程，每个循环中 KVL 的三个方程）：

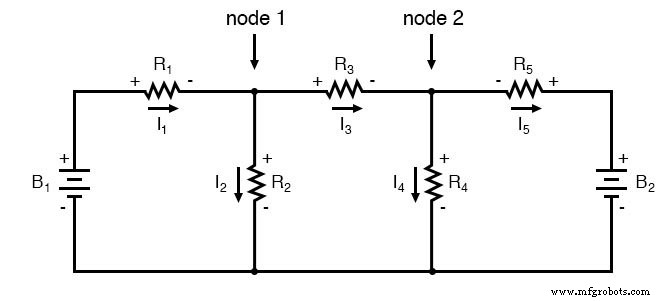
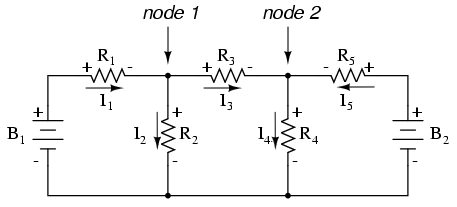
我想如果你没有什么比用五个方程求解五个未知变量更好的事情要做，你可能不介意使用这个电路的分支电流分析方法。对于我们这些拥有的人 更好地利用我们的时间，网格电流方法要容易得多，只需要解决三个未知数和三个方程：

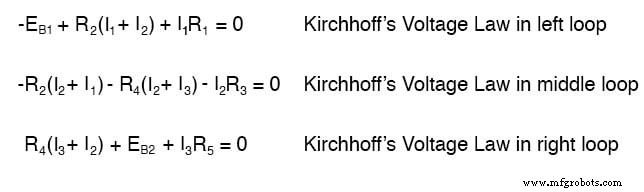
使用较少的方程是一个明显的优势，尤其是在手动执行联立方程求解时（无需计算器）。

不平衡惠斯通电桥

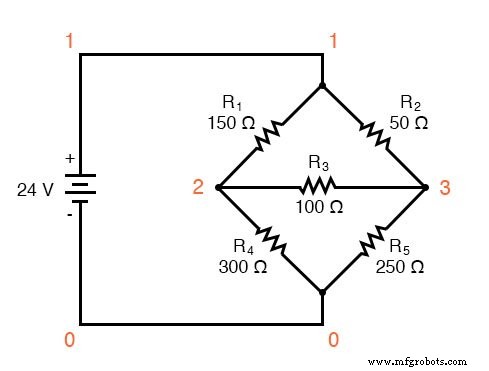
另一种非常适合网格电流的电路是不平衡惠斯通电桥。以这个电路为例：

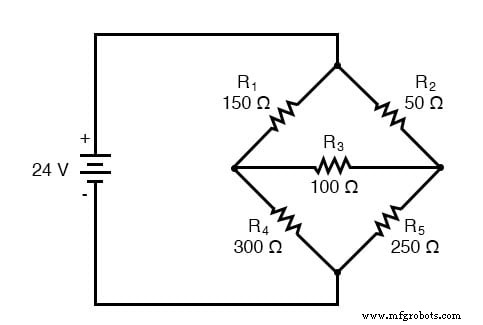
由于 R1/R4 和 R2/R5 的比率不相等，我们知道电阻器 R3 上会有电压，并且有一定量的电流通过它。正如本章开头所讨论的，这种类型的电路无法通过正常的串并联分析来简化，只能通过其他方法进行分析。

我们可以将分支电流方法应用于该电路，但它需要六个 电流（I1 到 I6），导致需要求解的非常大的联立方程组。然而，使用网格电流方法，我们可以用更少的变量求解所有电流和电压。

绘制网格

网格电流方法的第一步是绘制足够的网格电流以考虑电路中的所有组件。看看我们的桥式电路，应该很明显在哪里放置这些电流中的两个：

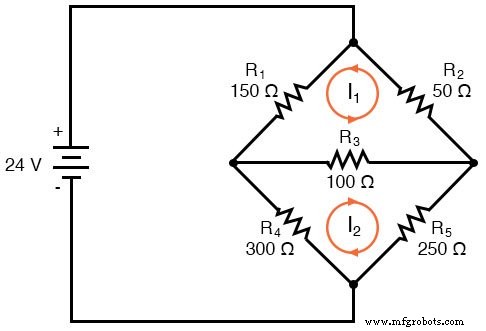
当然，这些网格电流的方向是任意的。然而，在这个电路中，两个网状电流是不够的，因为 I1 和 I2 都不通过电池。因此，我们必须添加第三个网格电流 I3：

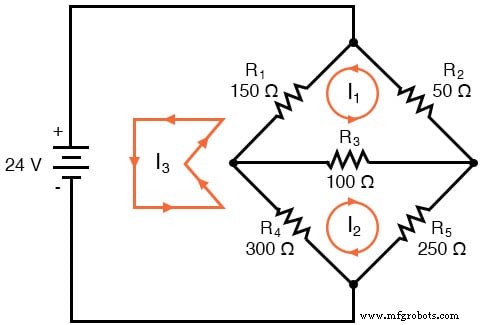
在这里，我选择了 I3 从电池底部循环，通过 R4，通过 R1，然后回到电池的顶部。这不是我为 I3 选择的唯一路径，但它似乎是最简单的。

标记电阻压降极性

现在，我们必须按照每个假定的电流方向标记电阻器电压降的极性：

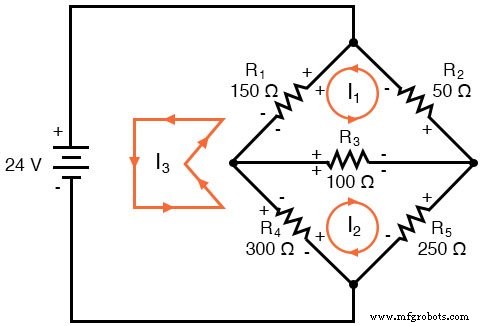
请注意这里非常重要的一点：在电阻器 R4 处，各个网状电流的极性不一致。这是因为这些网状电流（I2 和 I3）以不同的方向通过 R4。这并不排除使用 Mesh Current 分析方法，但它确实有点复杂。虽然稍后，我们将展示如何避免 R4 电流冲突。 （见下例）

使用 KVL

为桥的顶部环生成KVL方程，从顶部节点开始，顺时针方向追踪：

在这个方程中，我们用它们的总和来表示电流的共同方向 通过普通电阻。例如，值为 100 Ω 的电阻器 R3 的压降在上述 KVL 方程中由表达式 100(I1 + I2) 表示，因为电流 I1 和 I2 从右到左流经 R3。电阻 R1 也可以这样说，其压降表达式显示为 150(I1 + I3)，因为 I1 和 I3 从下到上通过该电阻，从而一起 产生其电压降。

为电桥底部环路生成 KVL 方程并不容易，因为我们有两个电流通过电阻器 R4 相互对抗。这是我的操作方法（从右侧节点开始，逆时针追踪）：

请注意方程原始形式中的第二项如何将电阻器 R4 的值为 300 Ω 乘以差值 I2 和 I3 (I2 - I3) 之间。这就是我们如何表示两个网格电流以相反方向通过同一组件的组合效果。选择合适的数学符号在这里非常重要：300(I2 - I3) 与 300(I3 - I2) 的意思不同。我选择写 300(I2 - I3) 是因为我首先想到的是 I2 的影响（产生一个正压降，用虚拟电压表测量 R4，底部红色引线和顶部黑色引线），其次I3 的影响（产生负压降，底部为红色，顶部为黑色）。如果我首先考虑 I3 的影响，其次考虑 I2 的影响，将我想象中的电压表引线保持在相同的位置（底部红色，顶部黑色），表达式将是 -300(I3 - I2 ）。注意这个表达式是 数学上等同于第一个：+300(I2 - I3)。

嗯，这需要处理两个方程，但我仍然需要第三个方程来完成我的三个变量、三个方程的联立方程组。这第三个方程还必须包括电池电压，到目前为止，在前面的两个 KVL 方程中都没有出现该电压。为了生成这个方程，我将用我想象中的电压表从电池的底部（负极）端子开始，顺时针步进（同样，我步进的方向是任意的，不需要与方向相同）再次追踪一个循环该回路中的网格电流）：

解决电流

使用我们喜欢的任何联立方程方法求解 I1、I2 和 I3：

示例： 使用 Octave 从上述简化形式的方程中找到 I1、I2 和 I3 的解。

解决方案： 在开源 Matlab® 克隆 Octave 中，将系数输入到方括号之间的 A 矩阵中，列元素以逗号分隔，行元素以分号分隔。在列向量中输入电压： b．未知电流：I1、2 和 I3 由命令计算：x=A\b。这些包含在 x 列向量中。

<前> 八度：1>A =[300,100,150;100,650,-300;-150,300,-450] 一 =300 100 150 100 650 -300 -150 300 -450 八度：2> b =[0;0;-24] 乙 =0 0 -24 八度：3> x =A\b x =-0.093793 0.077241 0.136092

I1 的负值告诉我们该网格电流的假定方向不正确。因此，通过每个电阻器的实际电流值如下：

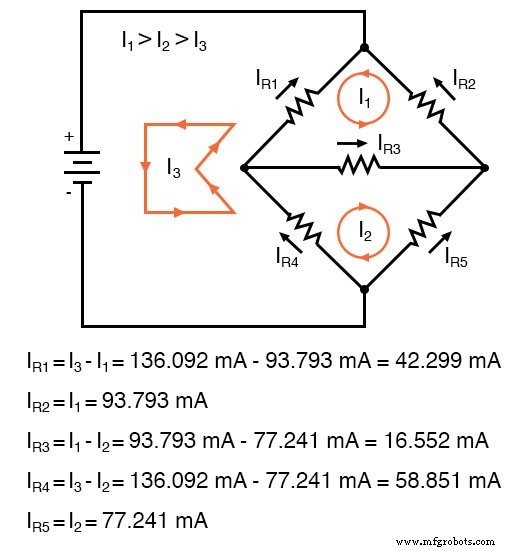
计算每个电阻上的压降：

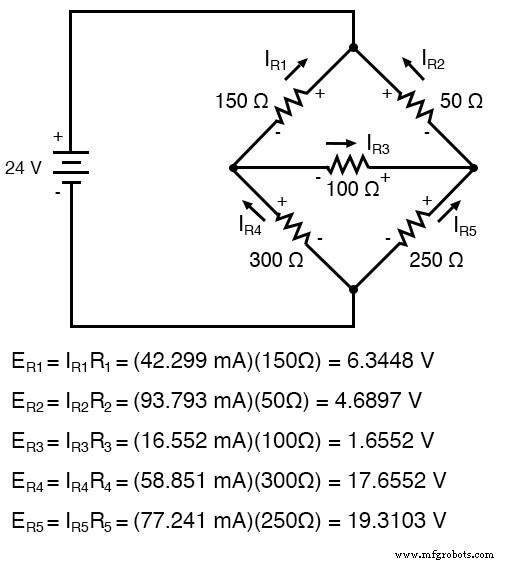
SPICE 仿真证实了我们电压计算的准确性：

不平衡惠斯通电桥 v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) 。结尾 v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E​​+01 1.931E+01 

示例：

(a) 为电流 I3 找到一条新路径，与 I1 或 I2 相比，该路径不会在任何电阻器上产生冲突的极性。 R4 是有问题的组件。 (b) 找出 I1、I2 和 I3 的值。 (c) 找出五个电阻电流并将它们与之前的值进行比较。

解决方案：

(a) 路线 I3 通过 R5、R3 和 R1，如图所示：

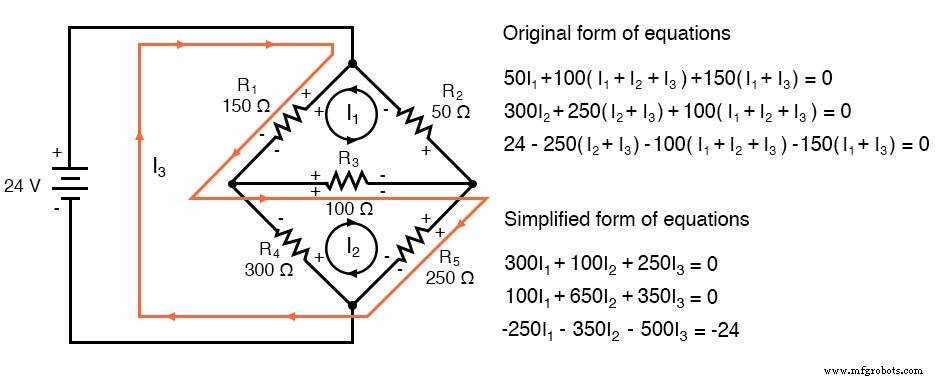
请注意，R4 上的冲突极性已被删除。此外，其他电阻都没有极性冲突。

(b) Octave，一个开源（免费）Matlab 克隆，在“x”处产生一个网格电流向量：

<前> 八度：1> A =[300,100,250;100,650,350;-250,-350,-500] 一 =300 100 250 100 650 350 -250 -350 -500 八度：2> b =[0;0;-24] 乙 =0 0 -24 八度：3> x =A\b x =-0.093793 -0.058851 0.136092

由于环路路径不同，并非所有电流 I1、I2 和 I3 都与之前的电桥相同 (I2) 但是，电阻电流与之前的值相比：

<前> IR1 =I1 + I3 =-93.793 毫安 + 136.092 毫安 =42.299 毫安 IR2 =I1 =-93.793 毫安 IR3 =I1 + I2 + I3 =-93.793 毫安 -58.851 毫安 + 136.092 毫安 =-16.552 毫安 IR4 =I2 =-58.851 毫安 IR5 =I2 + I3 =-58.851 毫安 + 136.092 毫安 =77.241 毫安

由于电阻电流与之前的值相同，因此电阻电压将相同，无需重新计算。

评论：

• “网格电流”分析方法要遵循的步骤：
• (1) 在电路的回路中绘制网格电流，足以说明所有组件。
• (2) 根据网格电流的假定方向标记电阻器压降极性。
• (3) 为电路的每个回路写出 KVL 方程，在方程的每个电阻项中用乘积 IR 代替 E。当两个网格电流通过一个组件相交时，如果电流以相同的方向通过该组件，则将电流表示为这两个网格电流的代数和（即 I1 + I2）。如果不是，则表示电流的差异（即 I1 - I2）。
• (4) 求解未知的网格电流（联立方程）。
• (5) 如果任何解为负，则假定的当前方向是错误的！
• (6) 代数相加网格电流以找到共享多个网格电流的电流分量。
• (7) 求解所有电阻器上的电压降 (E=IR)。

目测目测

我们再看一遍“网格电流法”，所有电流都顺时针 (cw) 运行。其动机是通过忽略电阻压降极性来简化网格方程的编写。但是，我们必须注意电压源相对于假定电流方向的极性。电阻电压下降的符号将遵循固定模式。

如果我们为下面的电路编写一组常规的网状电流方程，我们确实注意电阻两端的电压降的符号，我们可以将系数重新排列为固定模式：

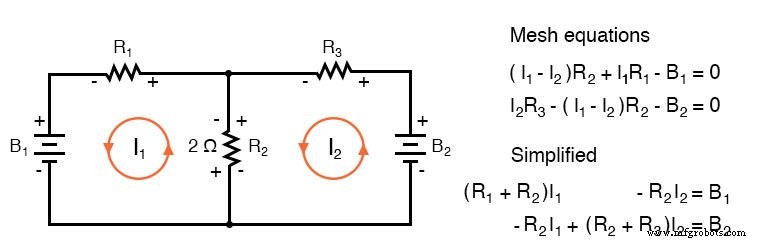
一旦重新排列，我们可以通过检查写出方程。系数的符号在上面的一对或下面的规则中的三个集合中遵循一个固定的模式。

网格当前规则：

• 此方法假设传统的电流流动电压源。将任何与电阻并联的电流源替换为与等效电阻串联的等效电压源。
• 忽略电阻上的电流方向或电压极性，绘制穿过所有组件的逆时针电流回路。避免嵌套循环。
• 根据未知电流写出电压定律方程：I1、I2 和 I3。公式 1 系数 1、公式 2、系数 2 和公式 3 系数 3 是各个回路周围电阻器的正和。
• 所有其他系数都是负数，代表一对回路共有的电阻。等式 1 系数 2 是回路 1 和 2 共用的电阻器，系数 3 是回路 1 和 3 共用的电阻器。对其他等式和系数重复此过程。
• +(R's loop 1的总和)I1 - (common R loop 1-2)I2 - (common R loop 1-3)I3 =E1
  -(common R loop 1-2)I1 + ( R 循环的总和 2)I2 - (共同的 R 循环 2-3)I3 =E2
  -(共同的 R 循环 1-3)I1 - (共同的 R 循环 2-3)I2 + (R 的循环 3 的总和)I3 =E3
• 等式的右侧等于电子电流流动电压源。相对于逆时针假设电流的电压上升为正，0 表示没有电压源。
• 求解网格电流方程：I1、I2 和 I3。使用 KCL 求解通过各个电阻器的电流。使用欧姆定律和 KVL 求解电压。

虽然上述规则特定于三网格电路，但这些规则可以扩展到更小或更大的网格。下图说明了规则的应用。三个电流都以相同的方向，顺时针方向绘制。为三个循环中的每一个编写一个 KVL 方程。请注意，电阻上没有极性。我们不需要它来确定系数的符号。虽然我们确实需要注意电压源相对于电流方向的极性。 I3 顺时针电流从 l24V 电源的 (+) 正极端子流出，然后返回到 (-) 端子。这是常规电流的电压上升。因此，第三个方程右边是-24V。

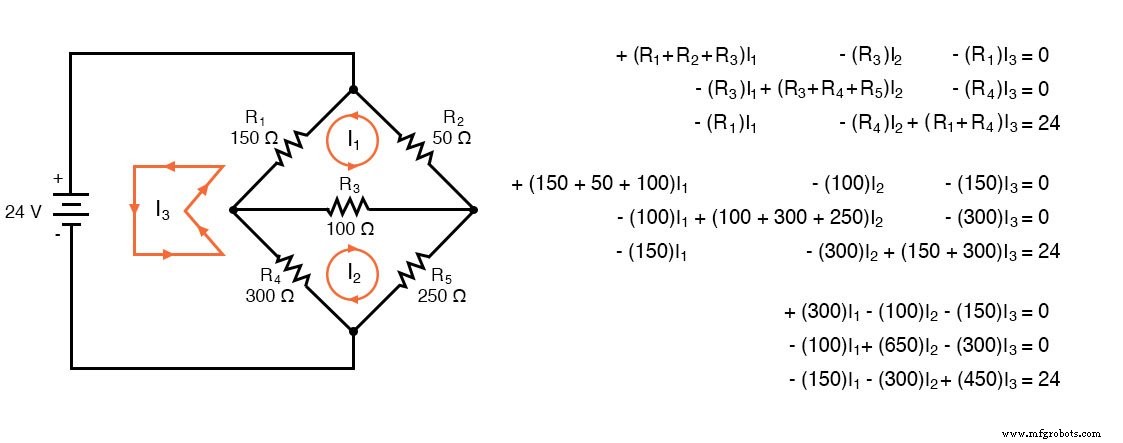
在 Octave 中，将系数输入到 A 矩阵中，列元素以逗号分隔，行元素以分号分隔。将电压输入到列向量 b 中。使用以下命令求解未知电流：I1、I2 和 I3：x=A\b。这些电流包含在 x 列向量中。正值表示三个网格电流均沿假定的顺时针方向流动。

<前> 八度：2> A=[300,-100,-150;-100,650,-300;-150,-300,450] 一 =300 -100 -150 -100 650 -300 -150 -300 450 八度：3> b=[0;0;24] 乙 =0 0 24 八度：4> x=A\b x =0.093793 0.077241 0.136092

网格电流通过不同的网格电流方法匹配先前的解决方案。电阻器电压和电流的计算将与之前的解决方案相同。此处不再赘述。

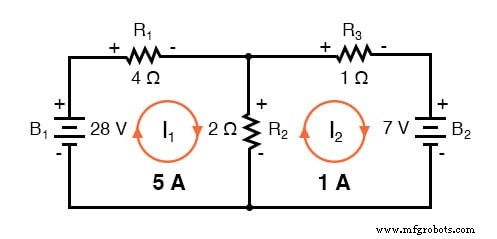
请注意，电气工程文本基于常规电流。这些文本中的回路电流、网格电流方法将运行假定的网格电流顺时针 .常规电流通过电路从电​​池的（+）端子流出，返回到（-）端子。传统的电流-电压上升对应于通过任何电压源跟踪从 (-) 到 (+) 的假定电流。

下面是先前电路的另一个示例。环路 1 周围的电阻为 6 Ω，环路 2 周围的电阻为 3 Ω。两个回路共有的电阻为 2 Ω。注意方程对中 I1 和 I2 的系数。沿着假设的顺时针回路 1 电流通过 B1 从 (+) 到 (-) 对应于电子电流流动电压上升。

因此，28 V 的符号为正。回路 2 逆时针假设电流轨迹 (-) 到 (+) 通过 B2，即电压降。因此，B2 的符号为负，在第二个网格方程中为 -7。再一次，电阻器上没有极性标记。他们也没有考虑到等式。

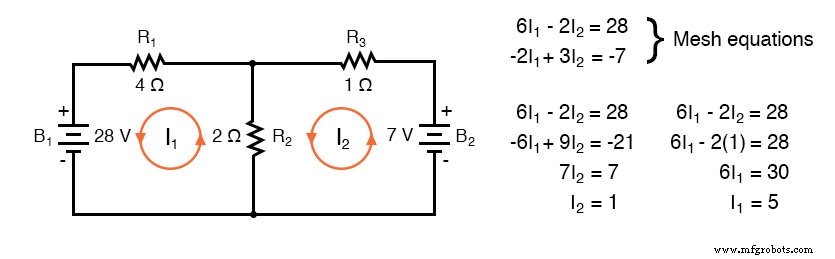
电流 I1 =5 A 和 I2 =1 A 都是正的。它们都沿顺时针方向流动。这与之前的结果相比。

总结：

• 修改后的网格电流方法避免了通过为常规电流顺时针绘制所有网格电流来确定方程系数的符号。
• 但是，我们确实需要确定回路中任何电压源的符号。如果假定的 ccw 电流与电池（源）一起流动，则电压源为正。如果假定的 ccw 电流流向电池，则符号为负。
• 有关详细信息，请参阅上述规则。

相关工作表：

• 直流网格电流分析工作表