简单向量加法
请记住,向量是数学对象,就像数轴上的数字一样:它们可以加、减、乘和除。加法可能是最容易可视化的向量运算,所以我们将从它开始。如果将具有公共角的向量相加,它们的大小(长度)相加就像常规标量一样:(下图)

同样,如果具有相同相位角的交流电压源串联在一起,它们的电压会增加,就像您对直流电池所期望的那样:(下图)
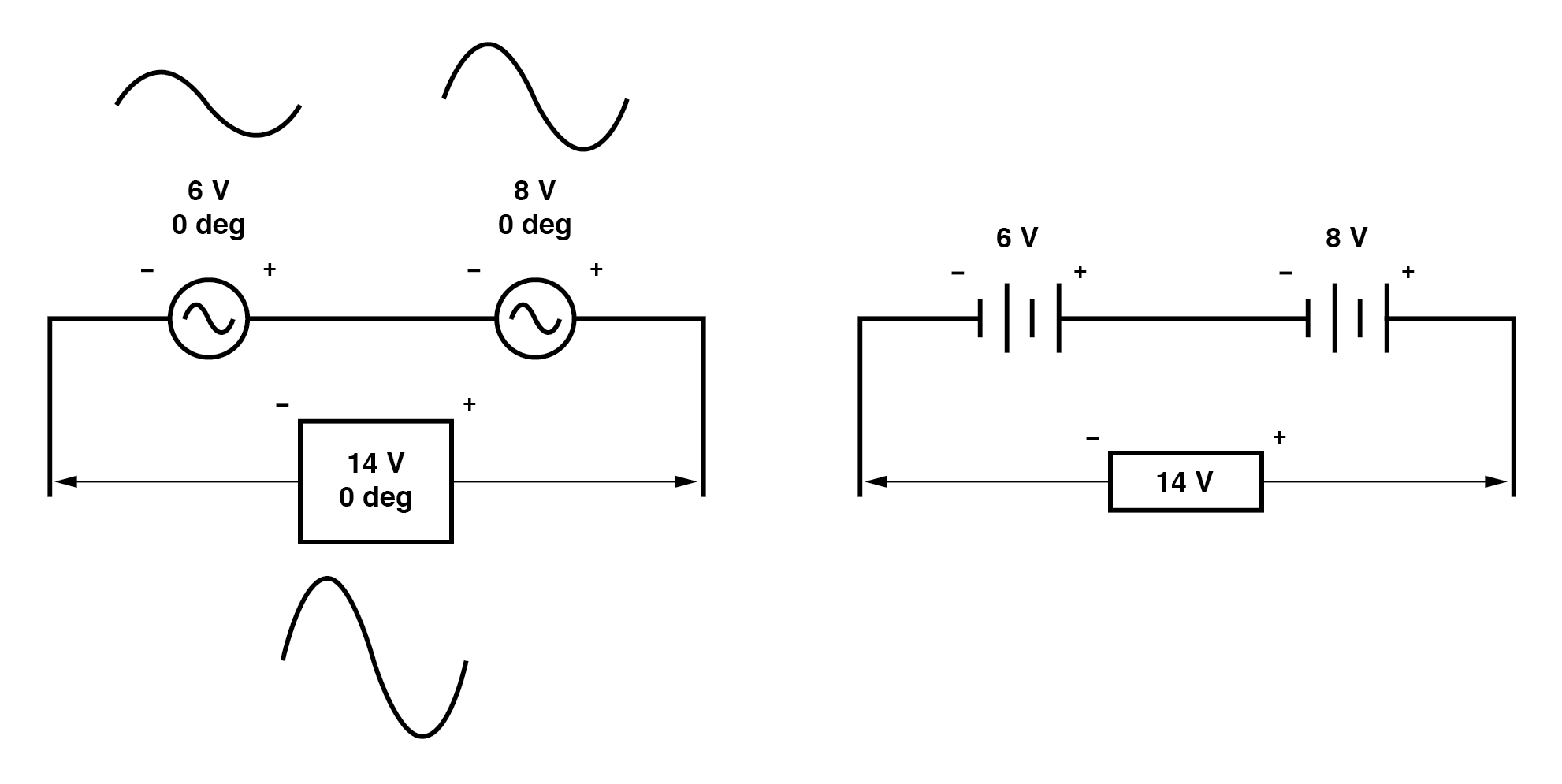
请注意两个交流电源引线旁边的 (+) 和 (-) 极性标记。尽管我们知道 AC 没有与 DC 相同意义上的“极性”,但这些标记对于了解如何参考给定的电压相角至关重要。这将在下一个示例中变得更加明显。
如果向量彼此直接相反 (180° 异相)相加,它们的幅度(长度)相减,就像相加时正负标量相减一样:(下图)
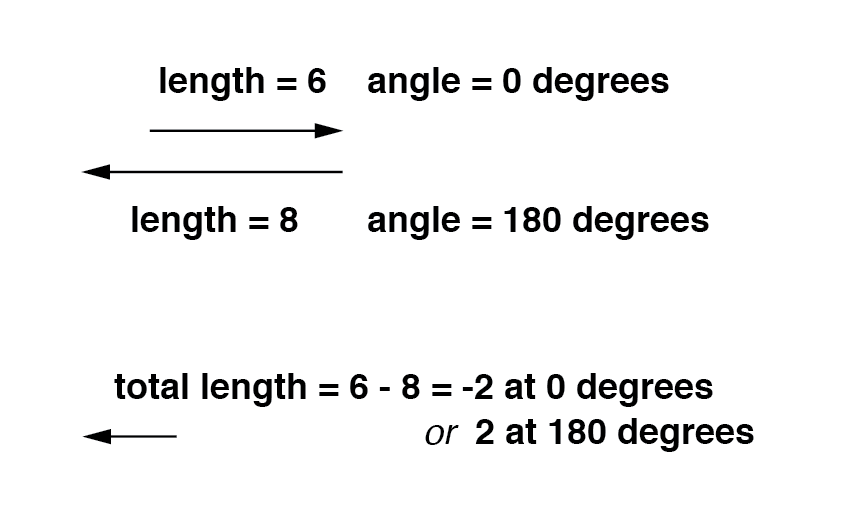
类似地,如果相反的交流电压源串联连接,它们的电压会减去,正如您在以相反的方式连接的直流电池所期望的那样:(下图)
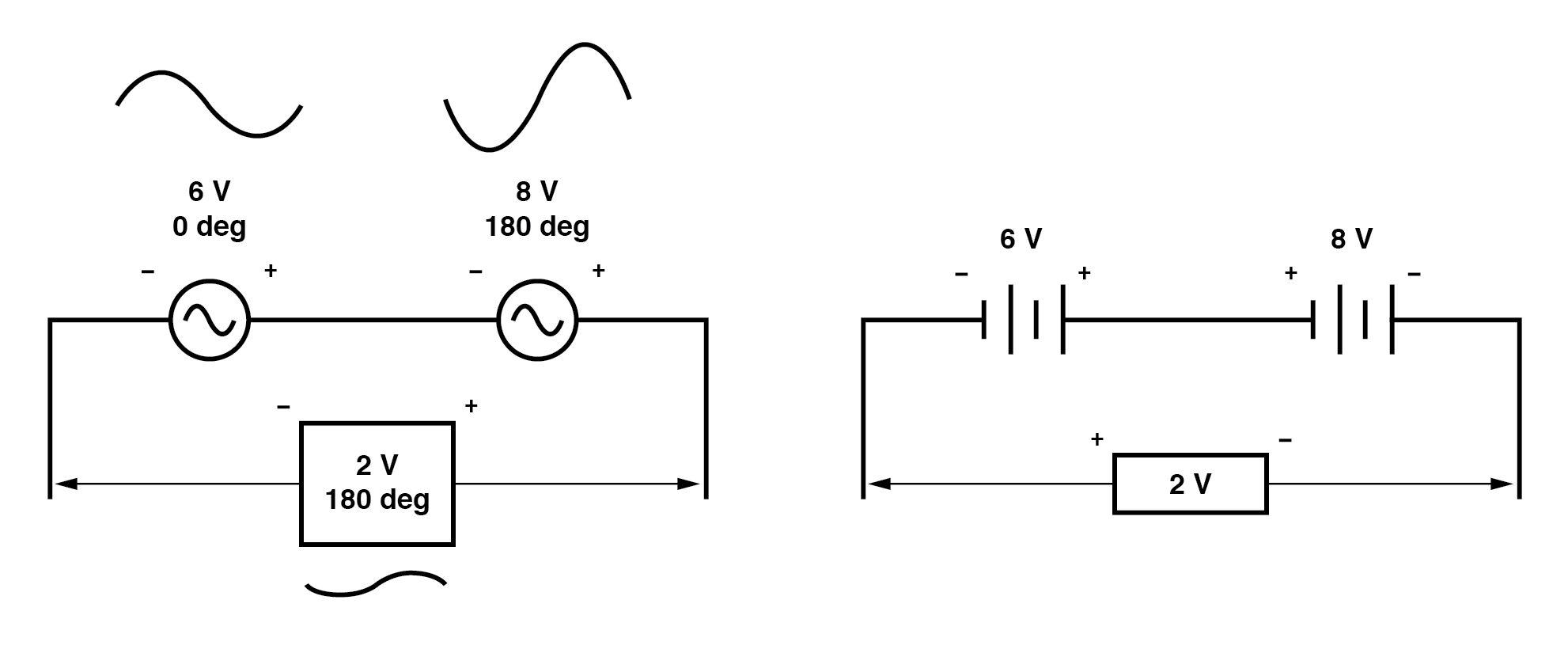
确定这些电压源是否彼此相反需要检查它们的极性标记和 它们的相角。请注意上图中的极性标记似乎表示附加电压(从左到右,我们看到 6 伏电源上的 - 和 +,8 伏电源上的 - 和 +)。
尽管这些极性标记通常表示添加剂 在直流电路中(两个电压一起工作以产生更大的总电压)的影响,在这个交流电路中,它们实际上是在相反的方向推动,因为其中一个电压的相位角为 0° 另一个相位角为180° .
结果当然是总电压为2伏。
我们也可以像这样串联显示相反的电压相减:(下图)
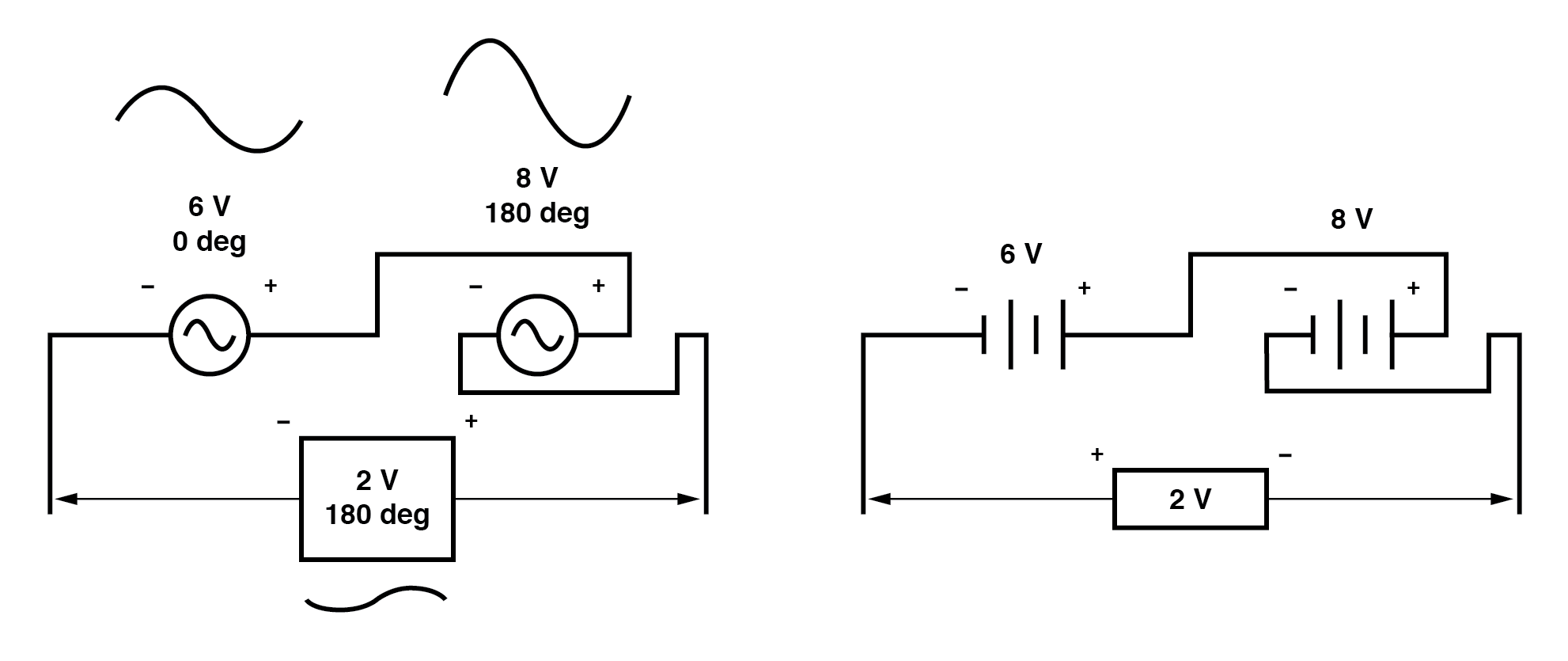
请注意,由于 8 伏电源上的接线颠倒,现在极性似乎是相反的。
由于两个源都被描述为具有相等的相位角 (0° ),它们确实是相互对立的,总体效果与前一种情况相同,具有“附加”极性和不同的相位角:总电压仅为 2 伏。 (下图)
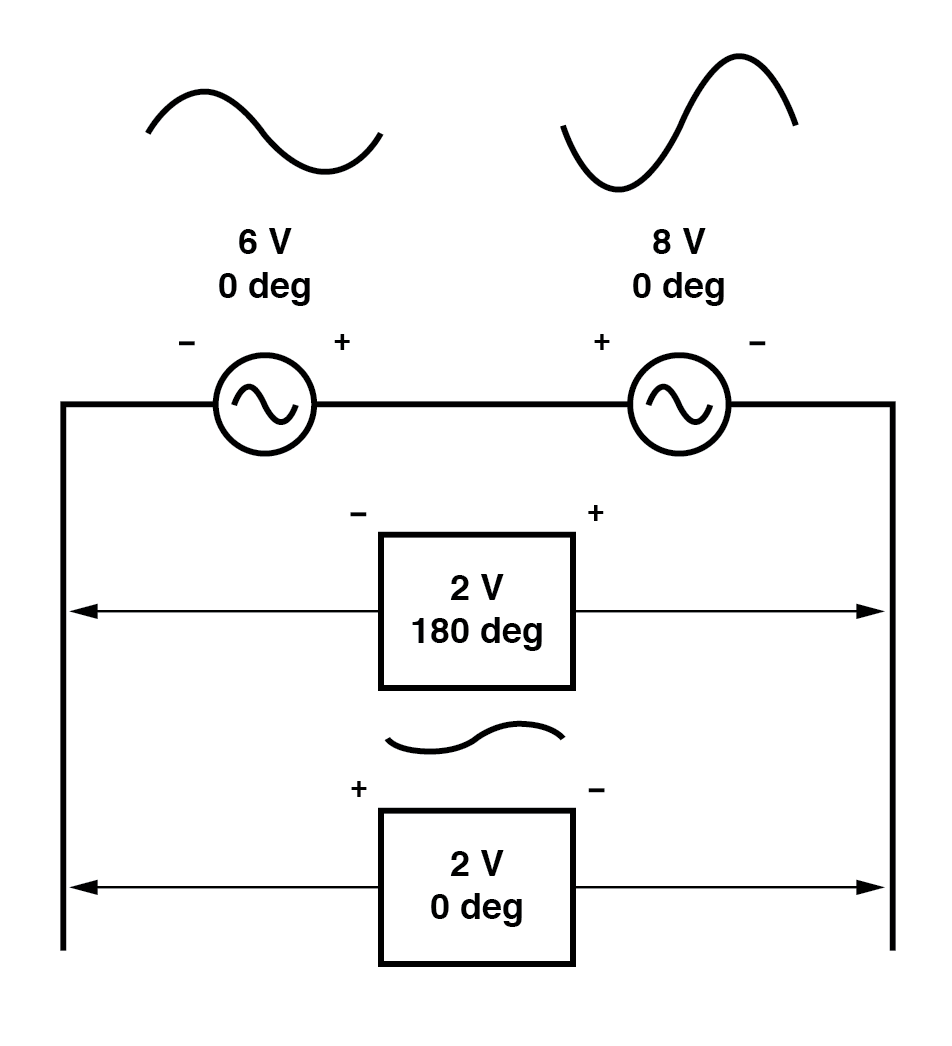
正如有两种方法可以表示源的相位一样,也有两种方法可以表示它们的总和。
所得电压可以用两种不同的方式表示:180° 时为 2 伏,左侧为 (-) 符号,右侧为 (+) 符号,或 0° 时为 2 伏,左侧为 (+) 符号和右侧的 (-) 符号。来自交流电压源的电线反转与将该电源相移 180° 相同。 (下图)

等效电压源示例。
相关工作表:
- 交流相工作表
- 交流网络分析工作表
工业技术


