基于聚二甲基硅氧烷交叉耦合衍射光栅的多自由度运动参数测量方法

背景

多自由度运动参数可以提供特定目标的准确位置和姿态信息，已广泛应用于大型结构的飞行器姿态稳定性控制、枪探针系统瞄准稳定性、机械臂工业加工中精密零件的对中和工件定位[1,2,3]。

因此，采用高精度检测方法来感知目标的多自由度信息（如直线度、俯仰度和偏转角），这些方法需要高性能传感器，包括高速检测的特性、同步、测量精度高、实时性好。这些方法被广泛应用于航空航天、无人机、精密制造和光学对准应用[4,5,6]。

动态多自由度运动信息的精确实时测量和解耦方法是确定载体姿态稳定性的关键要素。 Hsieh [7] 提出了一种三维检测阵列，使用三组模块来感知不同的自由度，其中使用不同的传感模块来测量不同的位置信息，并使用一种算法来计算角度和多自由度信息。 Liu [8] 提出了一种基于两个装配光栅之间相对角度变化的多自由度运动参数测量方法来进行信息测量。然而，上述方法容易出现两个或多个传感元件组装误差和耦合计算的复杂性，其精度还依赖于高精度仪器系统。

随着微纳制造技术、纳米技术和纳米材料的发展，研究人员从微型化和低成本应用的角度研究了基于单片机实现的多自由度运动参数检测方法。纳米材料、光学材料和纳米器件领域。 Tana [9] 报道了一种基于便携式微型棱镜结构的非衍射光束多自由度运动参数检测算法，可以最大限度地减少测量误差。我们团队提出了一种基于单个传感元件的矢量应变计方法，该方法可用于使用多轴集成机械传感器进行表面矢量应变测量，并为本文的研究奠定了基础[8, 10]。

在这项工作中，已经证明了一种基于单个元素的多自由度矢量位移和角度测量方法；该元件是使用氧等离子体处理技术制造的，在预弯曲成椭圆形的聚二甲基硅氧烷 (PDMS) 基板的两侧形成正交梯度光栅结构。这些交叉的光栅可以使输入激光束衍射成二维光斑阵列。衍射光斑位置信息可用于实现定位算法实时计算出的入射光束角。基于该方法和 480 × 640 像素电荷耦合器件 (CCD)，位移和偏转角的测量分辨率分别为 0.18 μm 和 0.0075 rad。此外，更高像素的 CCD 可以将位移和偏转角的测量分辨率分别提高到亚纳米和微弧度级别。最后，使用所提出的方法实时跟踪悬停旋翼机的动态位置；获取的信息可用于修正飞行器的位置，为飞行器在空中稳定提供了一种新方法。

实验

聚二甲基硅氧烷 (PDMS) 制备

PDMS (Sylgard 184) 购自 Dow Corning。 PDMS (10:1) 膜通过旋涂在硅片上制备，并在低于 80°C 的温度下旋转 2 小时后立即固化。通过控制旋转速度制备厚度为600 μm的PDMS基板。

双正交光栅制备

根据实验要求，制备面积为3×3 cm ² 的PDMS薄膜 .然后使用自制的平移台在 X 方向上将 PDMS 薄膜相对于原始薄膜预拉伸 1.5 倍。皱纹 SiO x 然后在氧气流速为 30 sccm 和氧化时间为 40 秒的条件下，在 O2 等离子体处理的预应变 PDMS 基板（IoN Wave 10，PVA-TePla，德国）上形成层。 PDMS基材表面经过预应变松弛后形成了均匀有序的纳米光栅结构。如图1a所示，在PDMS基板的另一侧以90°角差重复该工艺，在PDMS基板的两侧形成正交光栅结构。

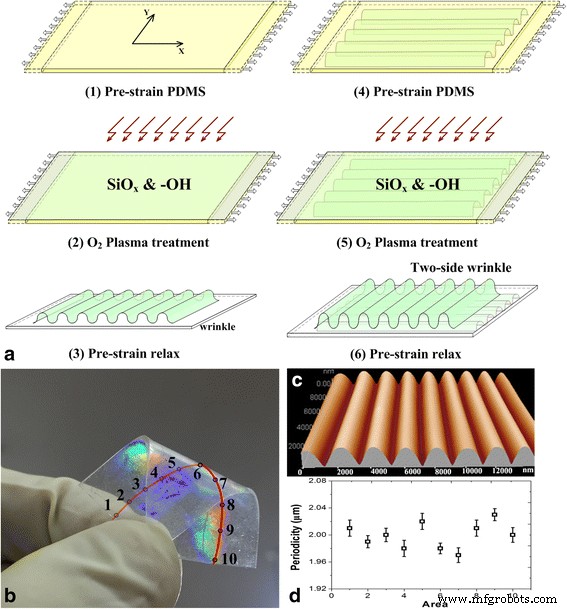
PDMS双光栅的制备工艺及形貌表征。 一 制作双光栅。 b 光栅的光学图像。 c 光栅的原子力显微镜图像。 d 样品的周期性均匀性

测试平台搭建

搭建的四自由度位移角传感器系统包括激光光源、角度位移平台组件、试样架、屏幕、CCD相机和计算机。如图 2a 所示，He-Ne 激光光源（激光波长 680 nm）安装在由电动旋转平台和手动三维调整架组成的角度位移平台组件（北京卓力仪器有限公司） .)该平台的旋转精度为 0.1°，位移精度为 2 μm。这种交叉光栅可以使激光束衍射成二维光斑阵列。使用480×640像素的互补金属氧化物半导体（CMOS）相机，使用MATLAB图像处理算法实时获取二维光斑阵列图像，提取每个衍射点位置，然后计算x- 和 y -轴位移和角度信息。提供了一个四旋翼飞机（Typhoon Q500，Yuneec Electric Aviation）形式的测试平台。并获取四自由度信息以获得室内悬停姿态。

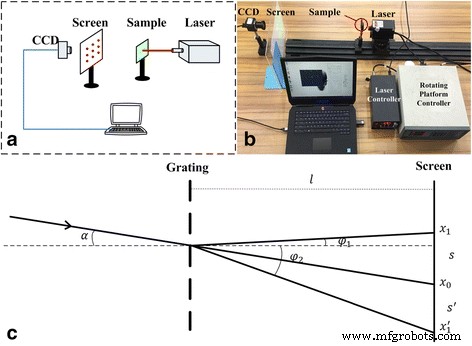
MODF运动参数的原理及测试系统。 一 系统图。 b 系统设置。 c 位移角度测试原理

分析与讨论

正交 PDMS 光栅表征

制造过程如图 1a 所示。 PDMS 的亲水表面改性使用氧等离子体技术。一氧化硅x 层和亲水基团（例如，-OH）因此通过氧等离子体在预弯曲的 PDMS 基材上形成。当 PDMS 衬底中的预应变超过临界值时，在预应变松弛后在 PDMS 表面形成光栅结构 [11, 12]。光栅的周期性是通过调整应用的预弯曲和等离子体条件来实现的，可以在我们以前的工作中计算出来。如图 1c 所示，微/纳米光栅的形貌通过原子力显微镜（AFM）（CSPM5500；Benyuan Co.）表征。如图 1b、d 所示，沿样品一侧的中心线选取了 10 个区域来研究光栅结构的周期性和均匀性。 10个区域的光栅对应的周期性是均匀的，在整个样品表面上的周期为（2±0.05）μm。

用于位置和角度运动参数表征的衍射光栅

根据夫琅禾费衍射理论[13]，激光束穿过样品（带有光栅）衍射成光斑矩阵。衍射斑的位置与入射光束的位置和角度直接相关，因此可以通过衍射斑的位置信息来检测入射光束的位置信息。

图 2 显示了移动和旋转平台以跟踪入射光束的定位和相应的衍射点。根据夫琅禾费衍射理论，当衍射光栅与屏幕距离固定时，入射光束、衍射光束与波长的关系可表示为：

这里，λ 是入射光束的波长，d 是光栅的周期，α 是入射角，φ 是衍射角，m 为光栅衍射级。

当入射角α 不等于0，“+”表示衍射光束和入射光束分布在光栅法线的同一侧，“-”表示衍射光束和入射光束存在于光栅法线的两侧。在特定的入射角下，屏幕上一阶衍射点和零级衍射点之间的距离不相等。因此，点之间的距离会随着入射角的变化而变化。通过计算衍射光斑位置，可以定量计算出入射光束的角度。同时，入射光束的移动位置导致衍射点的零级移动。入射光束位置信息可以通过衍射光束零级点的位置信息计算得到。

图 2c 显示了光栅衍射图的单一方向，其中 x 0 为一阶衍射点，x 1 和 \( {x}_1^{\hbox{'}} \) 表示衍射斑点的二阶。从图 2c 中，s 和 s ’是一阶和二阶衍射斑之间的距离，表示如下：

从方程。 (1):

由上式可得光束入射角与衍射斑纹间距的相关模型为：

基于正交衍射光栅的多自由度运动参数检测和表征

通过单向光栅的激光束可以形成单个衍射斑。当激光束穿过 PDMS 基板两侧的正交光栅时，可以形成正交取向。当光束沿屏幕一侧光栅的方向透射时，将形成一维光栅衍射光束，尺寸在x中设置 -轴。然后形成与 x 正交的一维光栅衍射光束 -axis 当光束沿着屏幕另一侧的光栅方向穿过时，然后在 y 中设置尺寸 -轴。在屏幕上形成二维衍射点阵列，如图3b所示。

MODF 运动参数取决于衍射点的运动。 一 一维衍射斑由单向光栅产生。 b 双交叉光栅产生二维光斑阵列。 c 光斑阵列的移动由激光源的移动来控制。 d 光斑阵列之间的间隙移动由激光束的入射角控制

当激光束的位置发生变化时，零级衍射光斑位置会出现相应的运动，根据夫琅禾费衍射理论，衍射位图的位置也会发生相应的变化。可以根据晶格运动的方向直接计算入射光束位置，然后检测光束沿x-的实现位置信息 和 y -轴。如图 3c 所示，由于位移和偏转的耦合效应，一阶衍射点位置无法准确计算光位移。此外，零级衍射点位置仅与源位置有关。因此，使用衍射点位移的零级来计算光源的位置会更准确。如图 3d 所示，入射光束沿 x 的偏转角信息 -axis 和 y -axis 可以通过光点在 x 上的距离来计算 -axis 和 y -轴基于角度与光斑变化之间的相关模型。

然而，衍射光斑位移原因的限制取决于入射角以及基于方程的光栅与屏幕之间的距离。 (1).在我们的作品中，光栅与屏幕固定在一起，这意味着光栅与屏幕之间的距离变化为零。激光源沿z方向移动时，衍射光斑无位移 -轴。同样，当激光源沿 z 旋转时 轴，入射角变化为零，这将导致衍射斑点不位移。

在我们的实验中，角度变化 (Δθ x ) 沿着 x -axis 可以根据列间距 (s x ,\( {s}_x^{\hbox{'}} \)) 的衍射点，角度变化（Δθ 是 ) 沿着 y -axis 可以根据列间距 (s 是 ,\( {s}_y^{\prime } \)) 的衍射点。调整组合平台以改变光源位置，然后每 0.02 s 由 MATLAB 软件获取相机图像以提取衍射光斑位置与早期值进行比较，用于计算 x -axis 和 y -axis 以及数组的列间距和行间距的变化。

基于该算法，可以通过处理运动前后的图像来分析光斑阵列的位移，计算Δx ,∆y , ∆θ x , 和 ∆θ 是 .由于图像中激光光斑包含多个像素，且其能量符合高斯分布，因此采用高斯分布拟合方法去除图像中的背景噪声，从而准确提取出激光光斑中心位置。激光光斑的高斯函数表示为：

在这里，我 (x , y ) 是光斑强度和 H 是振幅，(x 0, y 0) 为光斑中心坐标，σ 1、σ 2 是 x 上的标准差 -axis 和 y -轴，分别。

对上式两边取对数即可得到光斑中心位置，可表示为：

在这里，a , b , c , 和 d 为对现场所有像素进行高斯拟合得到的多项式系数。

通过运动前后的两幅图像计算了两个衍射点之间距离的变化。并将衍射光斑的中心光斑设置为运动前的坐标中心系：光斑的绝对位移坐标系和相对位移坐标系。衍射光斑的绝对位移坐标系以静止屏为参考。运动信息（Δx ,Δy ) 可以通过衍射点坐标的零级（即中心位置）计算出两个屏幕中的点阵。光斑相对位移坐标系以衍射斑零级为参考，可用于计算光斑阵列间距(S x ) 和行间距 (S 是 ).

图 4 显示了四个自由度的表征。当激光束沿着 x 割草时 轴，在 x 中有相应的衍射点阵运动 -axis，但 y 中的位移大约为零 -轴。位移的灵敏度约为 5.4 像素/微米。该方法可用于高精度计算光源沿轴的位置信息，如图4a所示。

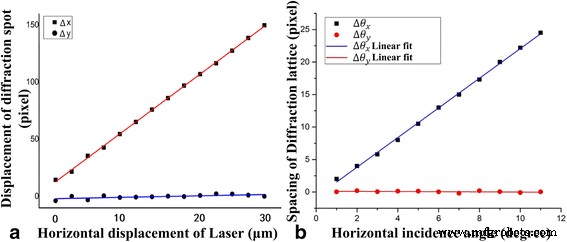
四个自由度的表征。 一 激光源的位移取决于衍射光斑的位移。 b 激光光源的入射角取决于衍射光斑之间的间隙

当激光沿 x 旋转一个小角度时 轴，衍射点阵行距有相应的距离变化，点阵列距为零。位移的灵敏度约为每角度 2.3 像素 (/°)。同时，由方程计算的角度测量范围理论上约为9.8°。 (1)–(5) 作为距离s =0. 归因于一阶衍射斑与零阶衍射斑随着入射角的增加，衍射斑的距离变化为零（s =0）。该方法可以实现光源沿x的角度信息 -轴。使用该方法也可以获得位置和角度信息。

一个像素的检测分辨率取决于基于MATLAB软件的算法。如上计算，该方法的位移灵敏度为 5.4 像素/微米，这意味着分辨率为 0.18 微米。 对于 2.3 像素/° 的位移灵敏度 ，它的分辨率为 0.0075 rad。这表明，基于此处介绍的方法和 CCD 分辨率，位移和角度的分辨率分别为 0.18 μm 和 0.0075 rad。 480 × 640 像素 CCD 用于实时获取二维光斑阵列的图像。此外，更高像素的CCD和光路的优化可以将位移和偏转角的分辨率分别提高到亚纳米和微弧度尺度。

悬停飞机旋翼运动参数信息表征

旋翼机是一种精度不高的民用无人机系统，广泛应用于航拍、航模、导航等领域。旋翼机的稳定性控制是无人作战平台的一个缩影。要实现高精度的飞行控制，最重要的是对飞机姿态和位置的稳定控制。其核心是实时解码高精度悬停姿态位置​​信息，使准确的悬停四自由度运动参数信息成为必不可少的资产。

在我们的实验中，基于交叉耦合衍射光栅，提出了一种实时获取飞机飞行四自由度姿态信息的测量方法。首先用四旋翼飞行器代替平台，由四自由度测试系统的位置和姿态组成，基于双光栅设置四自由度测试系统。 -四旋翼飞机的自由姿态测试系统。在测试系统中，一个小型激光指示器固定在四旋翼飞行器的中心作为光源，它垂直向下照射激光束。带有双光栅、屏幕和相机的样品沿光轴中心转动。这种交叉光栅可以使激光束衍射成二维光斑阵列。实验中，利用摄像头从屏幕上获取图像，并将图像实时传输至计算机，通过MATLAB软件计算位移信息。

为了实现对飞行信号的快速、准确、实时测量，四旋翼飞行器在空中盘旋并快速跟踪保持4秒的姿态信号。有关沿 x 的轴向位移的信息 -axis 和 y 已经在 4 秒的时间内获得了四旋翼飞机的 -axis，如图 5c 所示。在建立平面坐标系（即x -axis 和 y -axis)，x 和 y 值被转换为这些坐标点。 4 秒内的 200 个定位结果意味着在 0.02 秒内获得一个点。这表示每 0.02 秒实时使用飞机的跟踪方法来确定其位置和位置。飞机在 x 方向上的最大位移为 2.1 毫米 - 轴和 y 中的最大位移为 2.3 毫米 -axis，根据算法。

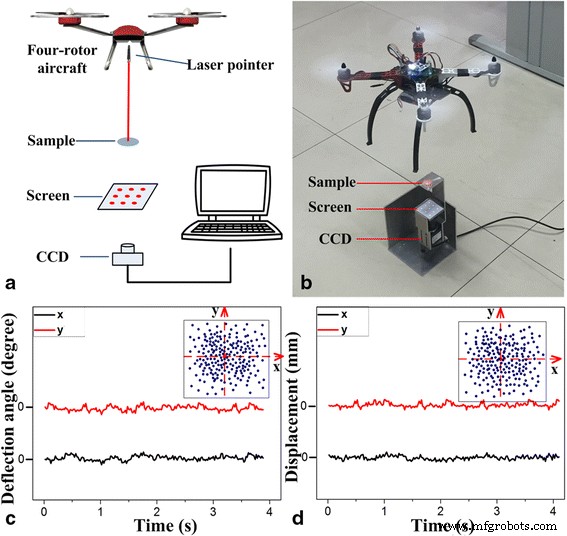
四旋翼飞行器姿态的表征。 一 系统图。 b 系统的设置。 c 旋翼飞行器的偏转角。 d 旋翼飞行器的位移

另外，飞机的俯仰角和滚转角信息已经通过上述算法和数据处理方法计算出来。如图 5d 的插图所示，四旋翼飞机的旋转角度点图通过每 0.02 秒实时跟踪，为飞机提供准确的角度信息。观察到飞机在 x 方向上的最大角度偏差为 1° -axis 和 y- 轴。因此该方法可以计算出飞行器的四自由度信息，在0.02s内将准确的位置和角度信号反馈给飞控系统，提高飞行器的稳定性。

结论

总之，展示了一种简单的可制造技术，可以在 PDMS 基板的两侧制造周期性为 2 μm 的正交光栅结构。基于正交光栅结构，研究了基于夫琅禾费衍射效应的衍射光斑位置信息识别光束位置和角运动参数信息的方法。使用 480 × 640 像素 CCD 实时获取二维光斑阵列的图像。结果表明，当使用这种方法和上述 CCD 时，位移和偏转角的分辨率分别为 0.18 μm 和 0.0075 rad。此外，使用更高像素的 CCD，位移和偏转角的分辨率可以分别提高到亚纳米和微弧度级。该方法可用于实时检测旋翼飞机的准确悬停位置和角度信息，每 0.02 秒的精度很高。这些信息可以反馈给无人机在空中控制飞行系统。该方法简单、成本低、精度高，可实现实时监控，为无人作战平台飞行器的稳定飞行和精确控制提供了研究基础。