B2 晶态 CuZr 合金中的各向异性相变

介绍

块状金属玻璃 (BMGs) 因其优异的机械和物理性能而备受关注，例如高强度、弹性、高硬度以及优异的耐腐蚀性等 [1,2,3,4]。然而，它们通常会通过局部剪切带发生灾难性的脆性断裂而失效 [5, 6]。在一些由延展性 B2 相 CuZr 颗粒增强的 CuZr 基块体金属玻璃复合材料 (BMGCs) 中，这一缺点在一定程度上得到了克服 [3, 7,8,9,10,11]。此外，一些 B2 结晶 CuZr 沉淀会通过在负载下在 CuZr 玻璃中结晶而固有地形成，然后发生孪晶和位错滑移，引起 BMGs 力学性能的变化，如实验 [12] 中所发现。为了对B2相CuZr析出物增韧BMGs并设计高性能BMGs，首先要明确B2相CuZr的变形行为。

B2相CuZr是一种形状记忆合金，在特定的热机械条件下具有恢复其原始形状的能力[13, 14]，不同于传统的以位错滑移或孪晶为主要变形机制的结晶材料[15,16,17]。基于泛函密度理论的第一性原理计算可用于研究吸附过程 [18,19,20] 和界面性质 [21, 22]，但不能用于研究相变行为的动态演化。受计算规模的限制。分子动力学 (MD) 模拟是研究材料力学性能和变形行为的有效方法 [23,24,25,26,27,28,29,30,31]。 Sutrakar 和 Mahapatra 研究了截面尺寸和温度对 Cu-Zr 纳米线相变的影响，以及通过 MD 模拟 [32,33,34] 的拉压不对称性，并获得了一些有价值的结果。例如，初始 B2 相通过 {100} 孪晶面的成核和传播转变为体心四方 (BCT) 相。阿米戈等人。等人在MD模拟中使用了两种势[35, 36]来研究相变行为，发现一种产生了从B2到BCT结构的马氏体转变，而另一种则没有[13]。

众所周知，晶体的各向异性在材料变形中起着重要作用。当沿不同晶体取向施加载荷时，不同的变形机制可能在变形过程中起主导作用 [37]。例如，完美的位错滑移和孪晶是分别使用圆柱形压头在氮化钒 (VN) 的 (001) 和 (111) 表面形成纳米压痕的主要变形机制 [38, 39]，显示出明显的各向异性塑性。对于 BCC 铁纳米线，相变显示出对晶体取向的复杂依赖，沿其施加载荷，<001> 取向的线表现出 BCC→FCC 转变，但 <011> 和 <111> 取向的线遵循 BCC→ HCP 转换 [40]。 B2结构中的原子分布阵列类似于BCC结构中的原子分布阵列，但B2结构中有两种元素。 BMGs中增强颗粒的晶体取向通常是分散的，因此加载方向对不同颗粒的增韧效果应该有不同的影响。因此，有必要研究增强粒子在不同方向加载时的变形行为。

单轴拉伸和压缩，作为通常用于评估材料基本机械性能的两种基本加载模式。在这项工作中，对 B2 结晶 CuZr 沿 [001]、[110] 和 [111] 取向的单轴拉伸和压缩试验进行了一系列 MD 模拟，以探索相变对加载取向和拉伸和压缩的依赖性(T/C) 不对称。

方法

选择众所周知的嵌入原子方法（EAM）[41]来描述Cu-Zr系统的原子间力。 EAM 电位已被广泛用于研究金属及其合金的机械性能 [42,43,44,45,46]。 2007年[35]、2009年[36]、2016年[47]，基于EAM框架，Mendelev等人对潜在参数进行了3次识别和优化。在这项工作中，使用了 2016 年开发的最新版本的 Cu-Zr [47] 原子间势中的参数。与2009年开发的参数相比，这些参数可以产生更真实的稳定和不稳定的堆垛层错能[36]，并且可以更好地描述晶体CuZr的性质。

加载轴向 z 的三个样本 分别沿[001]、[110]和[111]制备，如图1所示。加载前，采用共轭梯度（CG）算法最小化系统能量，达到优化的稳定配置。在 300 K 的室温下模拟机械测试。然后在 T 使用等温-等压 NPT 系综松弛系统 =300 K 持续 20 ps 以在无压力条件下达到平衡状态。发现随着应变率在5×10 ⁸ 之间变化，纳米多晶材料的应变率效应变得不显着。 和 1 ×10 ⁹ s ⁻¹ ，因此应变率指定为 1 × 10 ⁹ s ⁻¹ 通过综合考虑精度和计算效率 [48, 49]。因此，每个样本在 z 中被拉伸/压缩 -方向应变率为 10 ⁹ s ⁻¹ 装载期间；同时，采用带有机头/胡佛恒压器的 NPT 合奏 [50] 以保持 x 中的无压力 - 和 y - 方向。在松弛和加载阶段，在x中应用周期性边界条件 -, y -, 和 z -方向。

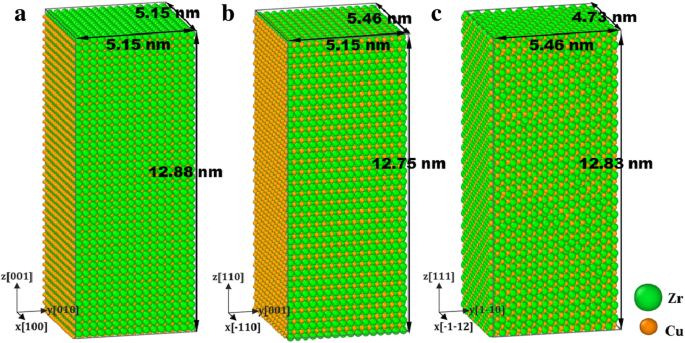
沿 a 轴向 z 的样本 [001], b [110] 和 c [111]，用原子类型着色

公共邻域分析 (CNA) [51] 是一种表征局部结构环境的算法，通常用作对晶体系统中的原子进行分类的有效方法。 BCC 结构中的第二最近邻距离仅比最近的距离大 15%；因此，CNA 方法在存在强烈的热波动和应变的情况下会失去一些可靠性。为了克服这个缺点，提出了多面体模板匹配（PTM）方法来对颗粒的局部结构环境进行分类并识别简单凝聚相（FCC、BCC、HCP等）的局部晶体结构[52]。与 CNA [51] 相比，PTM 方法在存在强烈热波动和应变的情况下具有更高的可靠性 [52]。 B2 和 BCC 结构具有类似的原子排列；因此，通过这种方法识别的BCC结构实际上是B2结构。用 PTM 对 MD 模拟获得的数据进行局部微观结构分析后，原子根据以下规则着色：蓝色为 BCC (B2) 结构，绿色为 FCC 结构，红色为堆垛层错或 HCP 结构，紫色为简单立方(SC)，白色表示晶界或位错核。需要注意的是，单层、双层和连续多层红原子分别表示为孪晶界、堆垛层错和 HCP 结构。含有红、绿、蓝、白原子的局部区域是无定形的。

作为一种补充的微观结构分析方法，中心对称参数（CSP）用于描述局部无序[53]。对于每个原子，CSP 的计算公式如下：

其中 N = 12 或 8 是 FCC 或 B2 结构中中心原子的第一个最近邻原子数，R 我 和 R i+N/2 是从中心原子到一对特定最近邻原子的向量。对于最近邻位于其完美晶格位置的原子，CSP 为零。如果原子附近存在空位或位错等缺陷，则原子的 CSP 将远大于局部原子振动引起的 CSP。 Stukowski[54]开发的开放软件Ovito用于显示原子构型。

结果和讨论

应力-应变曲线

图 2 显示了应力应变 (σ -ε ) B2 相 CuZr 沿 [001]、[110] 和 [111] 承受单轴拉伸和压缩的曲线。可以注意到应力比实验[55]大，因为（1）MD模拟使用的时间尺度与实验中使用的时间尺度不同，导致压痕速度比实验大得多； (2) 模拟中不考虑点缺陷、位错、晶界等缺陷。在初始阶段，这些曲线呈线性发展，然后呈现出不同的趋势。在第一个峰值之后，这些曲线可以分为三组。在第一组中，曲线迅速下降到低应力水平，例如沿 [110] 和 [111] 的压缩。在第 II 组中，应力下降到一个平台并随着第一个峰值后应变的增加而波动，例如沿 [001]、[110] 的张力和沿 [001] 的压缩。然后曲线在最终急剧下降之前攀升至第二个峰值。在第三组中，曲线迅速下降到低应力水平，然后以锯齿形波动，例如沿 [111] 的张力。在第一个峰之前，样品停留在 B2 结构中，没有观察到明显的位错滑移和孪晶现象，可以看作是弹性变形。在线弹性阶段，杨氏模量E 可以通过拟合每条曲线在0.00 <ε范围内的斜率得到 <0.02，并在表 1 中列出，其中可以看出 [001] 方向最软，[111] 方向最硬。这与散装 BCC 铁的结果一致 [40]。 E 除了[001]取向外，样品在压缩下的比在拉伸下的大，与在Cu单晶中观察到的一致[56]，这应该归因于压缩下更高的摩擦[56]。压缩下弹性阶段的其余曲线与拉伸下的曲线明显偏离，这应归因于原子间势的不对称拉伸和压缩性质[57]。在第一个峰值之后，尚不清楚变形应归因于位错滑移还是相变；因此，该区域不能被视为非弹性或塑性 T/C 不对称，这与其他人的作品不同 [57,58,59]。在流动部分，将详细讨论样品在不同方向加载时的变形机制。

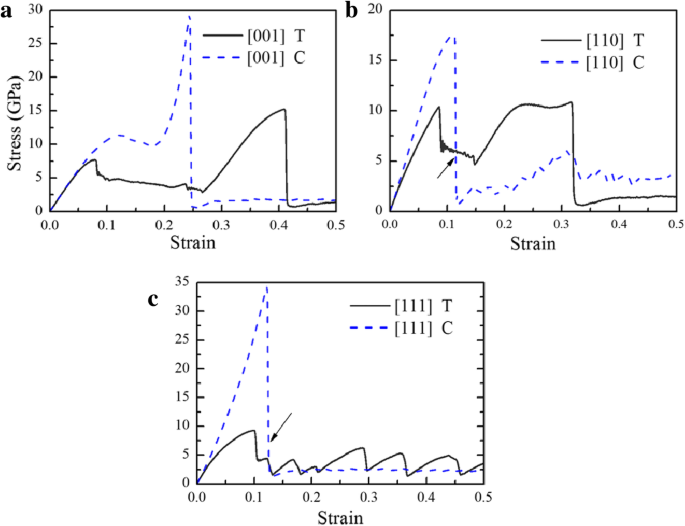
σ -ε 样品在拉伸 (T) 和压缩 (C) 下的曲线。 一 [001], b [110] 和 c [111]

失败行为

图3为沿[110]和[111]压缩样品的原子结构和径向分布函数(RDFs)，其σ -ε 曲线可以在图 2 中看到，标记为 [110] C 和 [111] C。图 3a、d 显示了在 300 K 弛豫后的初始样品 [110] 和 [111]，可以看出原子是在 B2 结构中。当 ε [110] C 和 [111] C 分别增加到 0.115 或 0.125，出现混合结构的区域，如图 3b、f 所示。混合区的结构定义为混合相。混合相的成核对应于图2b、c中曲线[110]C和[111]C的快速下降阶段，用箭头标记。因此，局部结构从 B2 到混合相的转变导致应力的快速下降。在流动阶段，混合相的体积分数变化是适应进一步变形的主要机制，压缩下样品的局部结构沿[110]和[111]在ε =0.25 分别显示在图 3c、g 中。为了指定混合区域中的结构，径向分布函数（RDFs ), g (r ），在不同应变下沿[110]和[111]压缩的样品如图3d，h所示。 g 的峰值 (r ) ε 处的样本 =0 和 ε =0.25 是尖锐的，表明它们仍然保持结晶特征。而 g 的峰值 (r ) 对于混合区域，即没有 B2 区域的样品，除了第一个区域外都是钝的，表明混合区域处于非晶态。位错提取算法（DXA）[60]也用于检测是否有位错形核，在整个变形过程中没有发现明显的位错。因此，B2 相的非晶化成为主要失效模式，导致快速下降，如图 2b、c 中箭头所示。

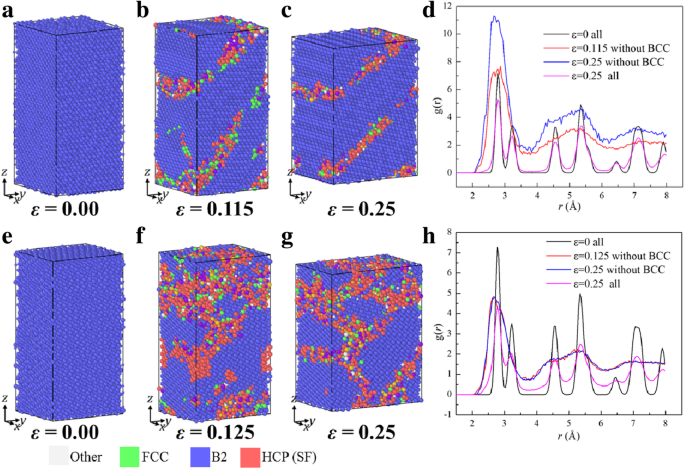
压缩下样品的原子构型和 RDF。 一 –d 沿着 [110] 和 e –h 沿[111]

图4显示了样品在沿[001]、[110]拉伸和沿[001]压缩的快速下降应变（失效应变）后的原子构型，其σ -ε 曲线属于组II。从图 4 中可以看出混合区的形成，类似于 I 组，表明非晶化也是主要的失效模式（图 4）。然而，这些混合区域被绿色和红色原子包围（FCC 和 HCP 结构），这与图 3 中的 B2 结构不同。这种差异表明混合相是由图 3 中的 B2 结构在压缩下转变的，但来自FCC的样品[001]在拉伸和压缩下，来自HCP的样品[110]在拉伸下。

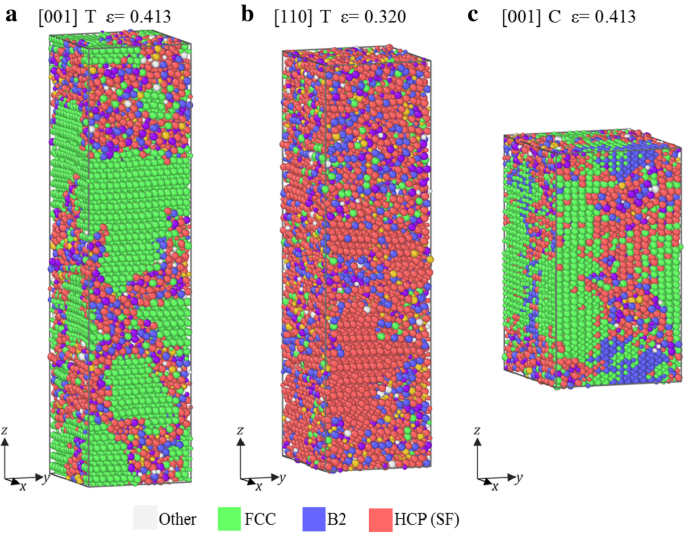
失效应变下样品中的原子构型。 一 在沿 [001] 的张力下，b 在沿 [110] 的张力下，和 c 在沿 [111] 压缩下

相变

图 5 显示了 σ -ε 样品 [001] 在张力下的曲线，其中还展示了典型点（用 A、B、...、G 标记）的微观结构。原子在 A 点 (ε =0.079) 属于 B2 结构，说明在 ε 之前 =0.079 样品中的变形是弹性的。然而，发生了从 B2 到 FCC 的局部转换，如 ε 的插图所示 =0.082 在图 5 中，导致第一次快速下降 (A→B) 到 ε =0.082，其中由于原子配置的重新分布而存储的弹性能量的释放提供了相变需要的能量。在B→F的流动阶段，随着相变的继续，储存的弹性能进一步释放，导致应力降低。样品的局部结构在ε处完全变成FCC =0.242（E 点）。 E点和F点之间的结构不断变化，但应力随着应变的增加而不断下降。为了揭示微观结构的变化，g的分布 (r ) 和原子数的变化 (N ) 反对CSP (N -CSP ) ε 处的样本 =0.242、0.254 和 0.267（E 点和 F 点之间）分别计算并显示在图 6a、b 中，其中每个峰的高度随着应变的增加而增加，表明系统变得更加紧凑。 <图片>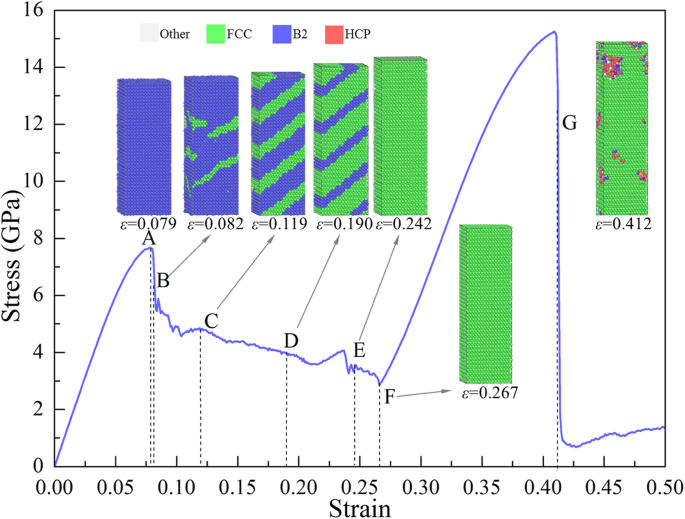

σ-ε 沿[001]拉伸样品的曲线，局部结构着色，蓝色、绿色和红色分别代表B2、FCC和非晶相

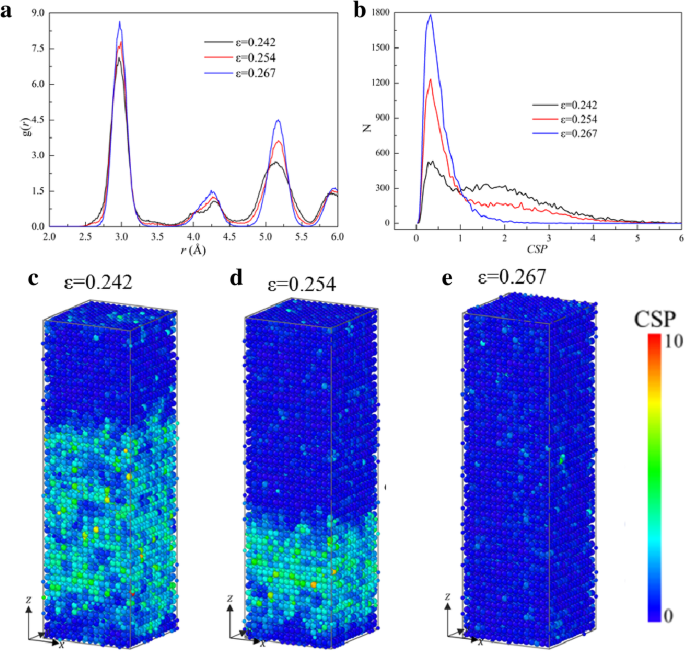
一 RDF , b N -CSP 样品在张力下沿 [001] 的图。 c –e CSP的分布 在不同菌株的样品中

为了表征原子是完美晶格的一部分还是局部缺陷（例如位错或堆垛层错）或表面，CSP [53] 具有 FCC 结构最近邻数 (N =12) 计算，如图 6c-e 所示。更大的 CSP 意味着与完美晶格的更大偏差 [17]。从图 6b 中可以看出，CSP <1 的原子数随着应变的增加而增加，从图 6c-e 中原子的 CSP 分布也可以更直观地看出这一点。不同于通常CSP不会随着应变的增加而降低的常见结果。因此，该阶段的主要变形行为也应归因于从不完美 FCC 到完美 FCC 的相变。在流动阶段，具有FCC结构的样品被拉伸，应力会增加，直到达到第二屈服点。然后曲线急剧下降，对应于局部非晶化，而不是位错或滑移的形核。

为了说明材料在变形过程中的相变，图 7 显示了一些 yoz 样品 [001] 在不同应变下的切片。水平和垂直的虚线用作识别原子结构是否旋转和偏离的参考。随着ε的增加 从 0.0 到 0.079，原子位于平行于水平和垂直轴的直线上，表明它们是 B2 局部结构。然而，图 7b 中的原子排列变为图 7c 中的原子排列为 ε 当一些 B2 结构转变为 FCC 结构时，从 0.079 到 0.119。阵列之间的角度从图 7b 中 B2 结构的 90° 变为图 7c 中 FCC 结构中的~ 85°，晶格取向顺时针偏离垂直轴 5°，但 B2 结构的原子阵列没有变化明显，无明显旋转。在 0.119 <ε < 0.190，FCC面积增大，绿色原子阵列逐渐逆时针旋转。在 ε =0.242，所有B2结构都转变为FCC结构，如图7e所示，其中三个晶格取向分别与三个轴几乎平行，但仍有明显偏差，表明FCC结构并不完美，即与图 6c 所示的一致。在流动阶段，原子排列有规律地趋向于，如图 7f 所示 ε =0.267，被认为是FCC结构的{110}面，其水平和垂直方向的晶体取向从B2结构的[010]和[001]变为FCC结构的<110>和<001>。

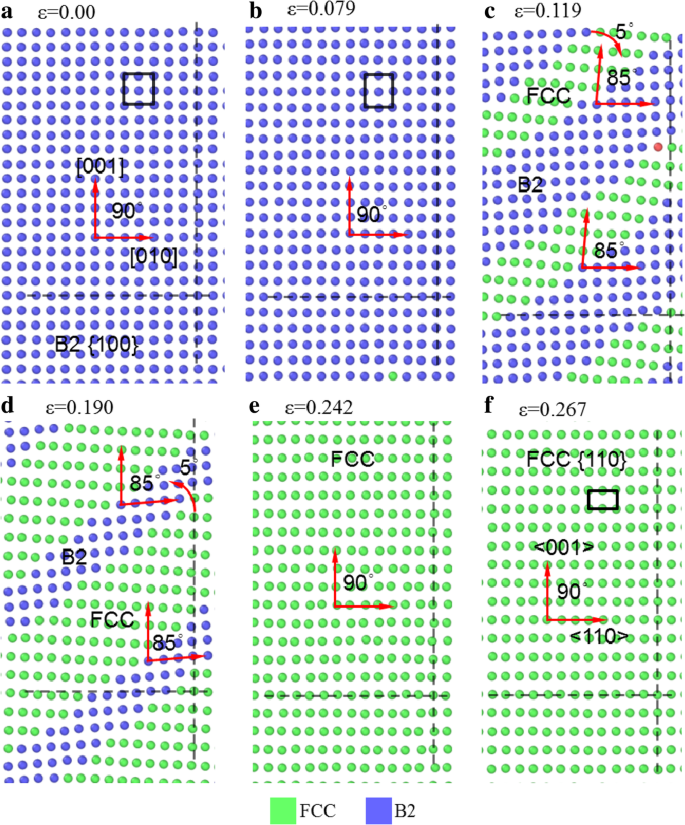
yz [001]样品在不同应变下的拉伸切片，局部晶格结构着色，蓝色、绿色和红色分别代表B2相、FCC相和非晶相

不同最大拉伸应变 (ε) 卸载时样品 (100) 响应的模拟 分别为 max =0.1、0.2 和 0.3)，并且 σ -ε 曲线如图 8 所示。可以看出卸载 σ -ε ε之间的曲线 =0.266 和 ε =0.056 不与加载曲线重叠，但它们可以满足弹性σ -ε ε 处的曲线 =0.056 然后沿弹性σ返回原点 -ε 曲线，表现出超弹性特性。加载和卸载路径形成滞后回线，这应该归因于正向和逆相变换的不同路径。

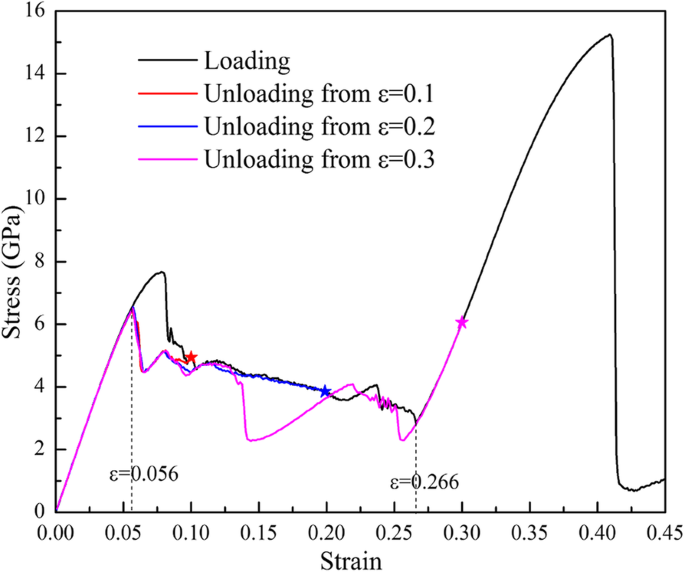
装卸σ -ε 不同应变沿[001]弯曲张力

σ -ε 样品[001]在压缩下的曲线也有类似趋势，如图9a所示，可分为四个阶段： (1) σ 随着应变的增加而线性增加； (2) σ 下降到平台期； (3) σ 随着应变的增加，以更大的斜率线性增加到第二个峰值； (4) σ 急剧下降到第二个高原。通过 PTM 分析局部结构，可以发现大多数原子在到达第二个峰之前被识别为 B2 结构，除了一些被识别为其他局部结构的分散原子，如图 9a 所示。但是，根据之前的理解，σ的突然变化 -ε 曲线通常对应于微观结构的变化。为了进一步确认，N -CSP 计算图并显示在图 9b 中，其中每个原子在不同应变下的 CSP 是用 B2 结构的最近邻 (N =8）。当 ε =0，CSP 原子数大于0但小于1，由于温度的影响，这意味着原子处于完美的B2结构。随着ε的增加 ，原子可以根据它们的 CSP 分为两组：CSP <1 和 5 ε < 0.121，第二个峰的 CSP 相同，但是这个 CSP 中的原子数 范围增加并趋于稳定，表明新相或缺陷（如堆垛层错）的形成。随着ε的进一步增加，第二个峰值处的CSP下降 ，即第二波向左移动。图 10 显示了不同应变下晶胞中键长的演变。在 ε =0，顶点处的八个 Cu 原子和体心处的一个 Zr 原子构成 B2 结构。晶格参数之间的关系为a =b =c .随着ε的增加 , xoy 中键的长度 平面增加，但在 xoz 平面减少。通过计算加载时其他两个方向的应变，可以发现在第二个峰值之前，其他两个方向的应变是相同的。因此，沿 x- 的键长 和 y -方向应该相同，并且大于沿 z 的方向 -方向。晶格参数之间的关系变为a =b> c .这些原子阵列可以被识别为 BCT 结构。综上所述，B2结构向BCT结构的转变是样品[001]受压变形的主要机制。

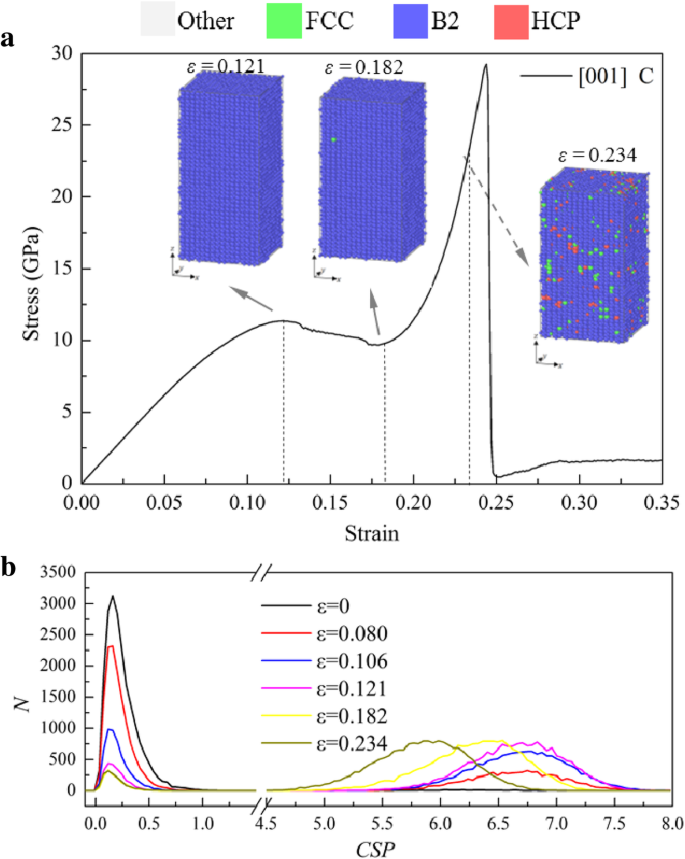
样品 [001] 在压缩下的响应。 一 σ-ε 曲线和典型的原子构型，原子用 PTM 识别的局部结构着色。 b N -CSP 地块

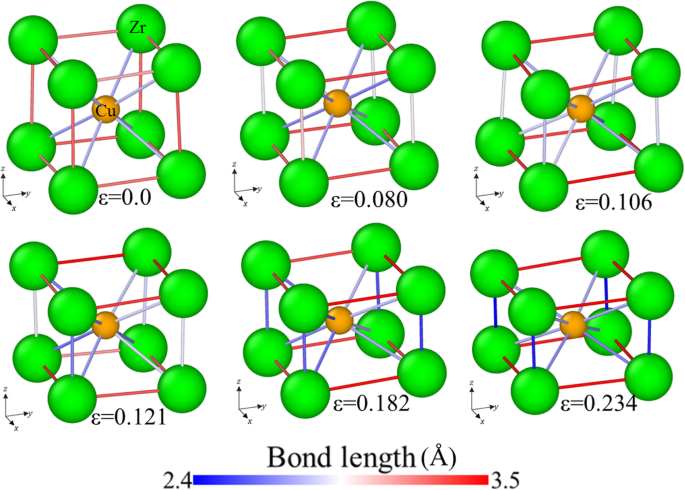
样品[001]在压缩下的键长变化，键长随其长度变化

图 11a 显示了样品 [110] 在张力下的响应。第一个峰值（A点）对应于B2结构的屈服极限，然后一些局部B2结构转变为HCP结构，导致急剧下降。随着ε的增加 ，当样品完全转变为 HCP 时，应力降低直到 C 点。图11b，c是xoy ε 处的一层切片 分别 =0 和 0.150，其中可以看到在初始阶段，Cu 和 Zr 原子位于相同的原子层中（图 11b）。然而，Cu 和 Zr 原子在 ε 处分离成相邻的层 =0.150（图 11c），这导致从 B2 到 HCP 的相变。然后随着ε的增加 , σ 以比初始线性阶段更小的斜率增加到 D 点，然后急剧下降到低应力水平，对应于由于局部非晶化导致的失效。

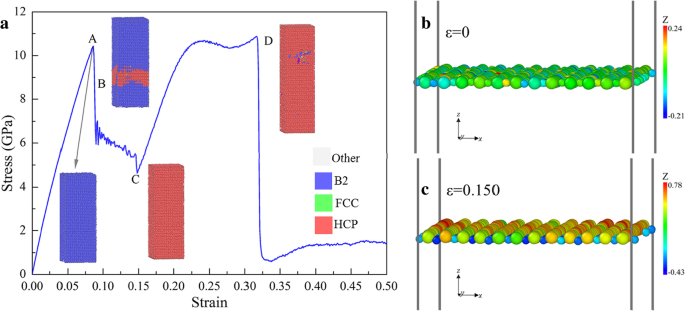
一 张力沿 [110] 的变形行为，用 PTM 着色。 b , c xoy 上的原子切片 分别在 ε =0 和 0.150 处的平面

结论

在这项工作中，利用分子动力学模拟，利用最新的原子间势，分别研究了沿 [001]、[110]、[111] 取向承受单轴拉伸和压缩的 CuZr 样品的响应和相变，其中可以得出以下主要结论：

1. 1.

   CuZr样品在拉伸和压缩下的力学响应表现出明显的不对称性，其主要失效机制应该是局部非晶化。

2. 2.

   拉伸和压缩沿[001]和拉伸沿[110]存在三种相变：B2→FCC、B2→BCT和B2→HCP。

3. 3.

   发现B2→FCC、B2→BCT和B2→HCP相变分别通过独特的机制实现，即晶格旋转（~ 5°）、均匀变形以及与Cu和Zr原子层分离。

4. 4.

   局部非晶化前卸载后相变区可恢复，表现出超弹性。

该结果对于探索纳米晶CuZr的力学性能和变形机制，以及纳米晶CuZr颗粒作为增强剂提高金属玻璃韧性的应用具有重要意义。

数据和材料的可用性

本研究中使用或分析的数据集可向相应作者索取。

缩写

密件抄送：

体心立方

BCT：

体心四边形

BMG：

大块金属眼镜

BMGC：

块状金属玻璃复合材料

CG：

共轭梯度

CNA：

共同邻居分析

CSP：

中心对称参数

铜：

铜

CuZr：

铜锆

DXA：

位错提取算法

EAM：

嵌入原子法

FCC：

面心立方

HCP：​​

六角密排

MD：

分子动力学

NPT：

粒子数、压力和温度恒定

PTM：

多面体模板匹配

RDF：

径向分布函数

条款/条件：

拉伸和压缩

VN：

氮化钒

锆石：

锆

ε ：

应变

σ ：

Stress