基尔霍夫电压定律 (KVL)

什么是基尔霍夫电压定律 (KVL)？

被称为基尔霍夫电压定律的原理 （由德国物理学家 Gustav R. Kirchhoff 于 1847 年发现）可以这样说：

“回路中所有电压的代数和必须为零”

通过代数 ，我的意思是考虑符号（极性）和大小。通过循环 ，我的意思是从回路中的一个点到该回路中的其他点，最后回到初始点的任何路径。

在串联电路中演示基尔霍夫电压定律

让我们再看看我们的示例串联电路，这次对电路中的点进行编号以供电压参考：

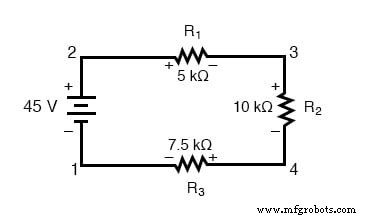
如果我们在点 2 和 1 之间连接一个电压表，红色测试线连接到点 2，黑色测试线连接到点 1，仪表将记录 +45 伏特。通常不显示“+”号而是隐含的，用于数字仪表显示中的正读数。但是，对于本课，电压读数的极性非常重要，因此我将明确显示正数：

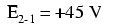
当电压用双下标（符号“E2-1”中的字符“2-1”）指定时，它表示第一点（2）处的电压，参考第二点（1）测量。指定为“Ecd”的电压表示数字表指示的电压，红色表笔在“c”点，黑色表笔在“d”点：“c”处的电压参考“d” .

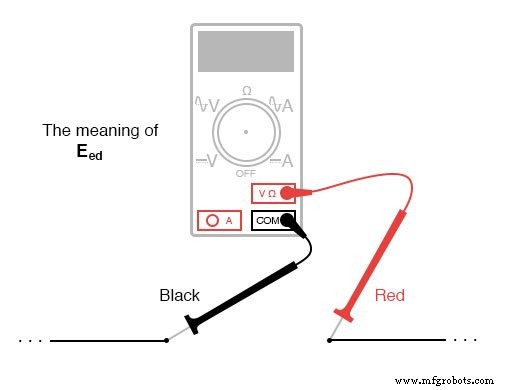
如果我们用同样的电压表测量每个电阻器上的电压降，以顺时针方向绕电路走动，仪表的红色测试线在前面，黑色测试线在后面的点，我们将获得以下读物：

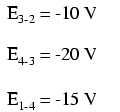
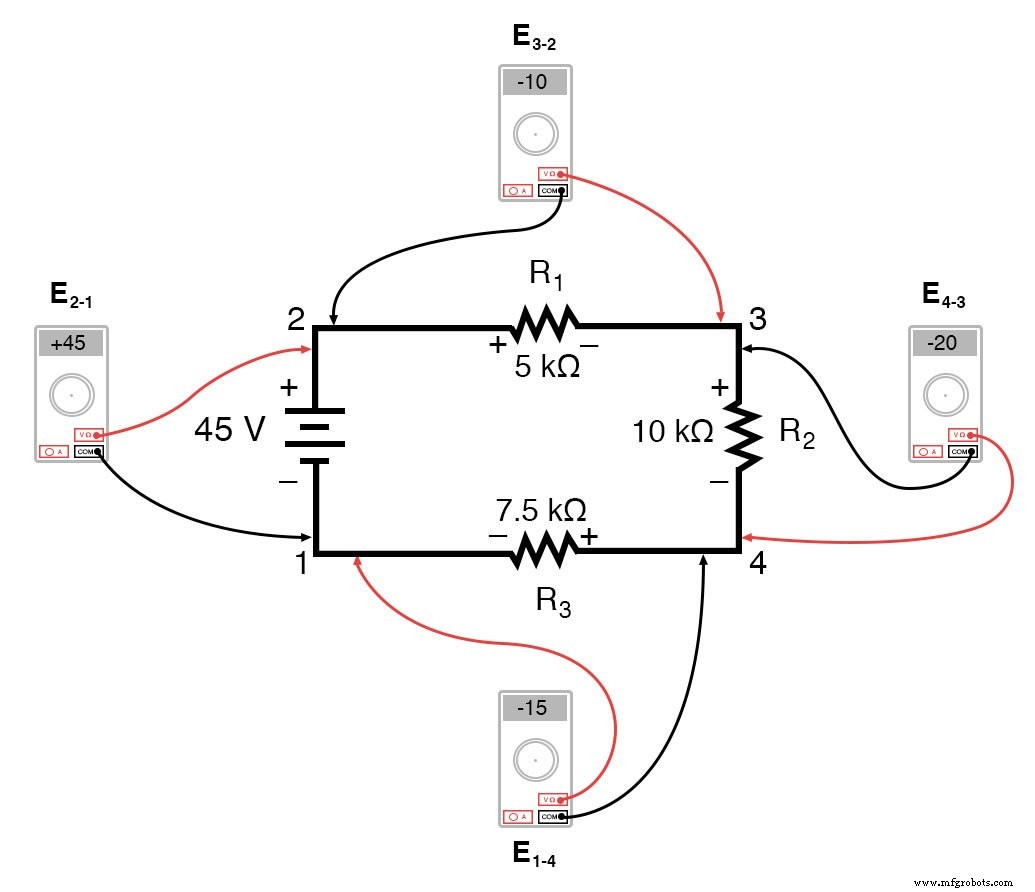
我们应该已经熟悉串联电路的一般原理，即单个电压降加起来等于施加的总电压，但是以这种方式测量电压降并注意读数的极性（数学符号）揭示了另一个方面原则：这样测量的电压加起来为零：

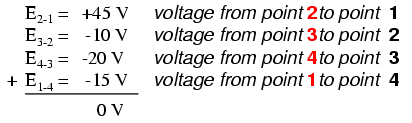
在上面的示例中，循环由以下点按此顺序形成：1-2-3-4-1。我们从哪个点开始或从哪个方向开始跟踪循环并不重要；电压总和仍将为零。为了演示，我们可以在同一电路的回路 3-2-1-4-3 中计算电压：

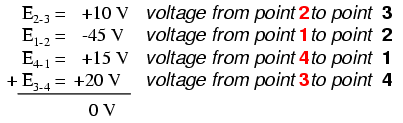
如果我们重新绘制示例串联电路，以便所有组件都用一条直线表示，这可能更有意义：

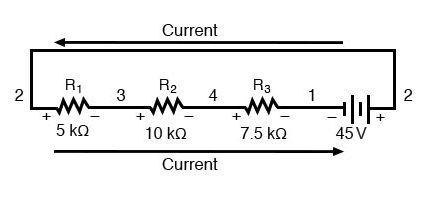
它仍然是相同的串联电路，只是组件以不同的形式排列。请注意电阻器电压下降相对于电池的极性：电池电压在左侧为负，在右侧为正，而所有电阻器电压降的方向相反：左侧为正，右侧为负。这是因为电阻电阻 由电池推动的电荷流动。换句话说，电阻施加的“推力”对抗 电荷的流动必须 与电动势源方向相反。

在这里，我们看到数字电压表将在该电路中的每个组件上指示什么，左侧为黑色引线，右侧为红色引线，以水平方式布置：

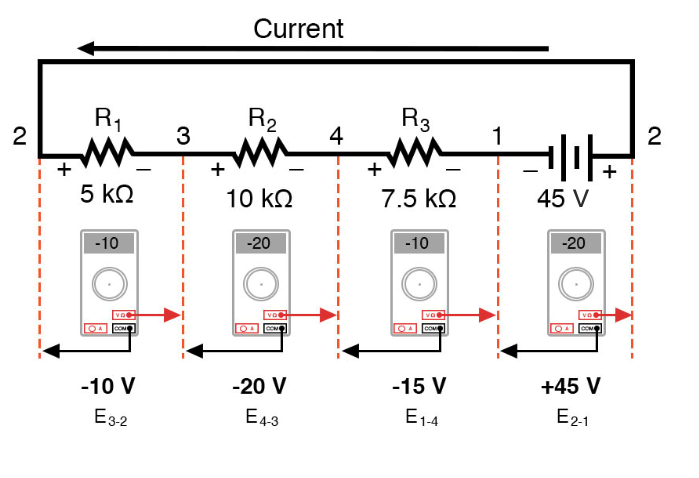
如果我们使用相同的电压表并读取组件组合的电压，从左侧唯一的 R1 开始，然后在整个组件串中进行，我们将看到电压如何以代数方式相加（至零）：

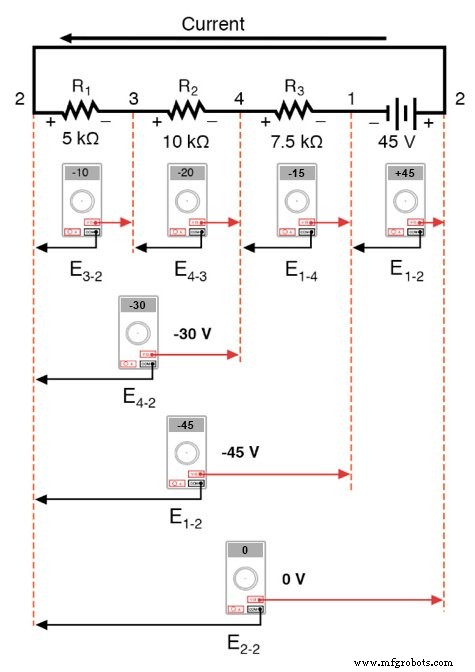
串联电压相加的事实应该并不神秘，但我们注意到极性 这些电压的不同在数字相加的方式上有很大的不同。在读取 R1—R2 和 R1—R2—R3 两端的电压时（我使用“双破折号”符号“—”来表示系列 电阻器 R1、R2 和 R3 之间的连接），我们看到电压如何连续测量更大（尽管为负）的幅度，因为各个电压降的极性在相同的方向（左正，右负）。

R1、R2、R3两端的压降之和等于45伏，与电池的输出相同，只是电池的极性与电阻压降的极性相反（左负，右正），所以我们结束在整个组件串上测得的电压为 0 伏。

我们最终应该在整个字符串中得到恰好为 0 伏的电压，这也不是什么秘密。看电路，我们可以看到最左边的串（R1的左边：2号点）直接连接到最右边的串（电池右边：2号点），根据需要完成电路。

由于这两个点是直接相连的，所以它们电气上是共同的 对彼此。因此，这两个电气公共点之间的电压必须 为零。

在并联电路中证明基尔霍夫电压定律

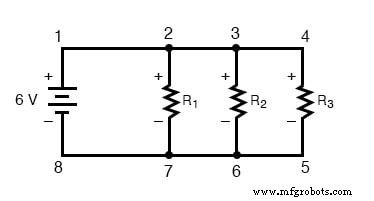
基尔霍夫电压定律（有时表示为 KVL 简而言之）将适用于任何 电路配置，不只是简单的串联。注意这个并联电路是如何工作的：

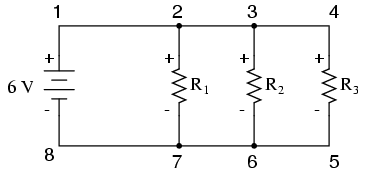
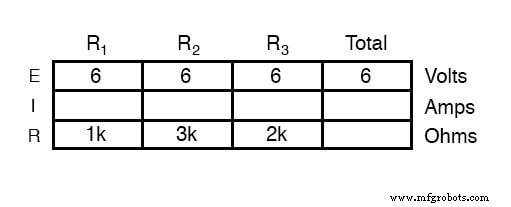
作为并联电路，每个电阻器上的电压与电源电压相同：6 伏。计算循环 2-3-4-5-6-7-2 周围的电压，我们得到：

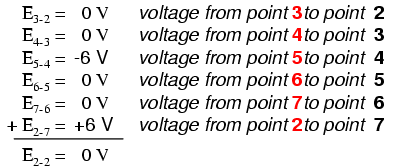
请注意我如何将最终（总和）电压标记为 E2-2。由于我们在点 2 开始循环步进序列并在点 2 结束，这些电压的代数和将与在同一点 (E2-2) 之间测量的电压相同，当然必须为零。

基尔霍夫电压定律的有效性，不考虑电路拓扑

该电路是并联而不是串联的事实与基尔霍夫电压定律的有效性无关。就此而言，电路可能是一个“黑匣子”——它的组件配置完全隐藏在我们的视野之外，只有一组暴露的端子供我们测量它们之间的电压——而 KVL 仍然适用：

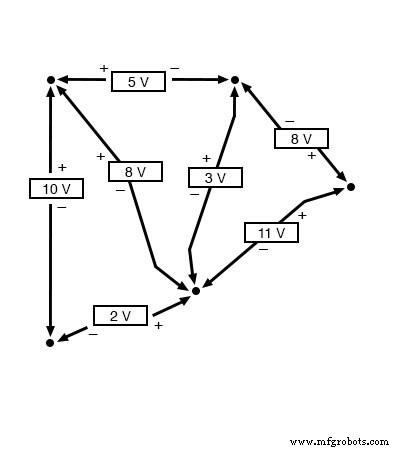
从上图中的任何终端尝试任何步骤顺序，回到原始终端，您会发现电压的代数和总是 等于零。

此外，我们为 KVL 追踪的“回路”甚至不必是闭路意义上的真实电流路径。为了遵守 KVL，我们所要做的就是在电路中的同一点开始和结束，计算下一个点和最后一个点之间的电压降和极性。考虑这个荒谬的例子，在同一个并联电阻电路中追踪“回路”2-3-6-3-2：

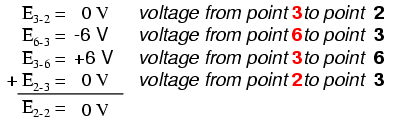
在复杂电路中使用基尔霍夫电压定律

KVL 可用于确定复杂电路中的未知电压，其中特定“回路”周围的所有其他电压都是已知的。以下面这个复杂的电路（实际上是两个串联电路在底部用一根导线连接起来）为例：

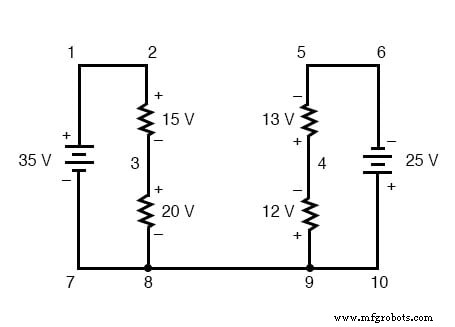
为了使问题更简单，我省略了电阻值，并简单地给出了每个电阻器上的电压降。两个串联电路在它们之间共享一根公共导线（导线 7-8-9-10），从而在 之间进行电压测量 两个电路都可以。如果我们想确定点 4 和 3 之间的电压，我们可以建立一个 KVL 方程，其中这些点之间的电压为未知数：

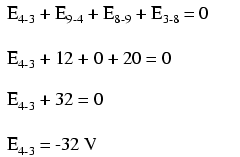
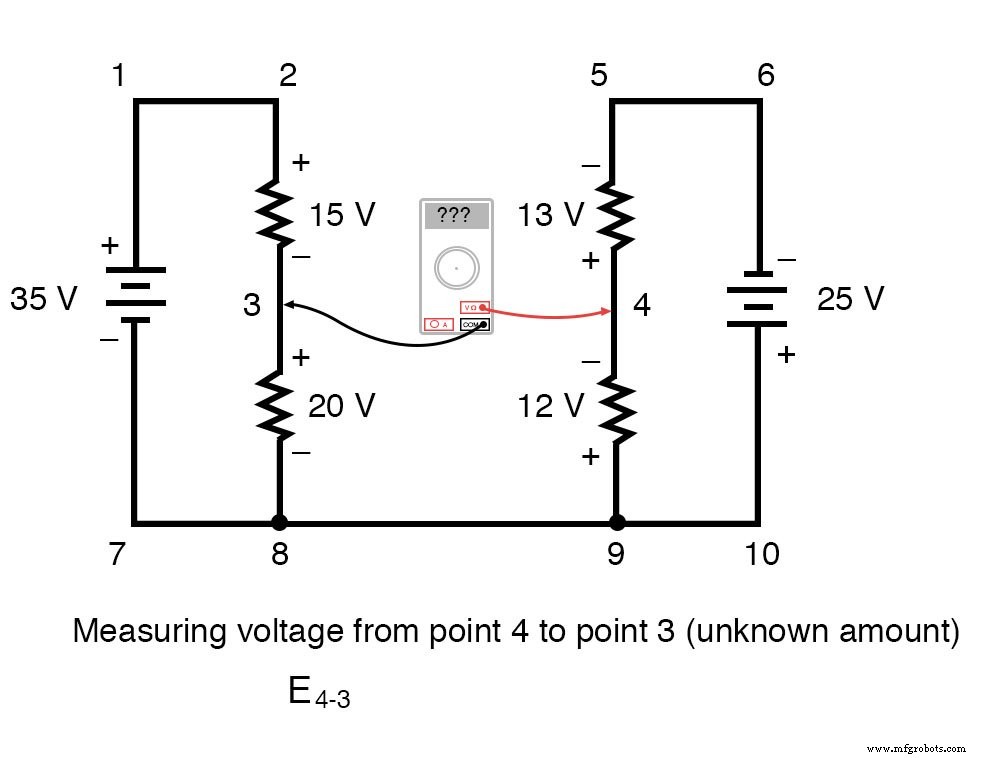
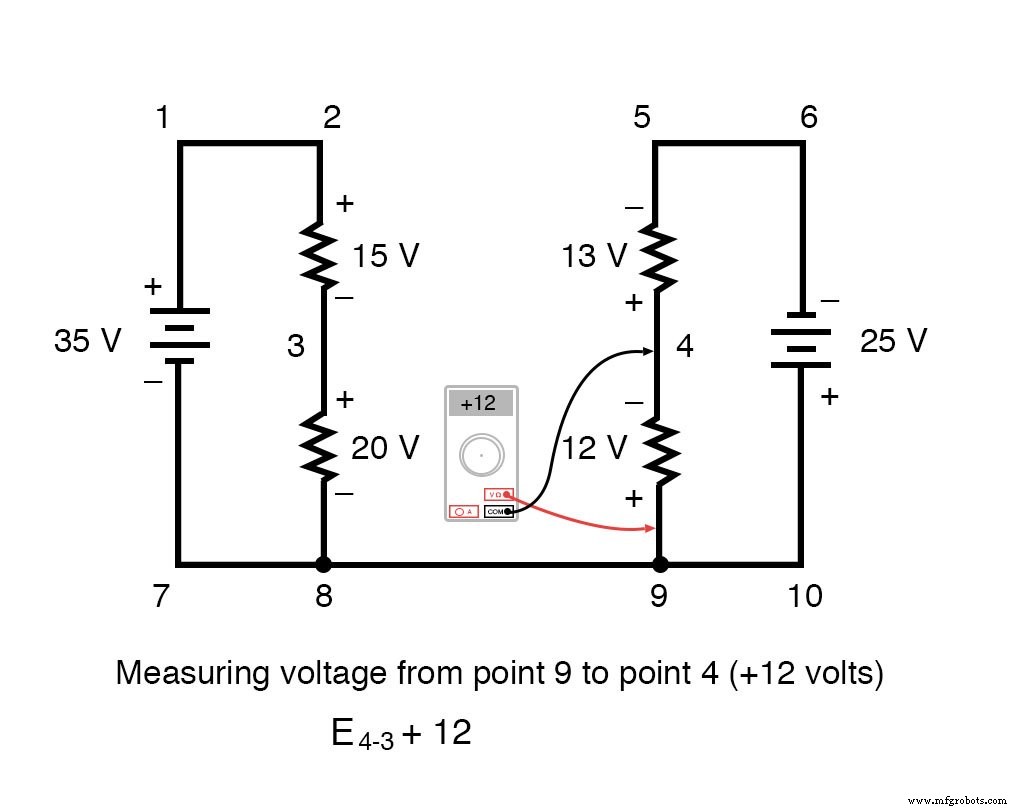
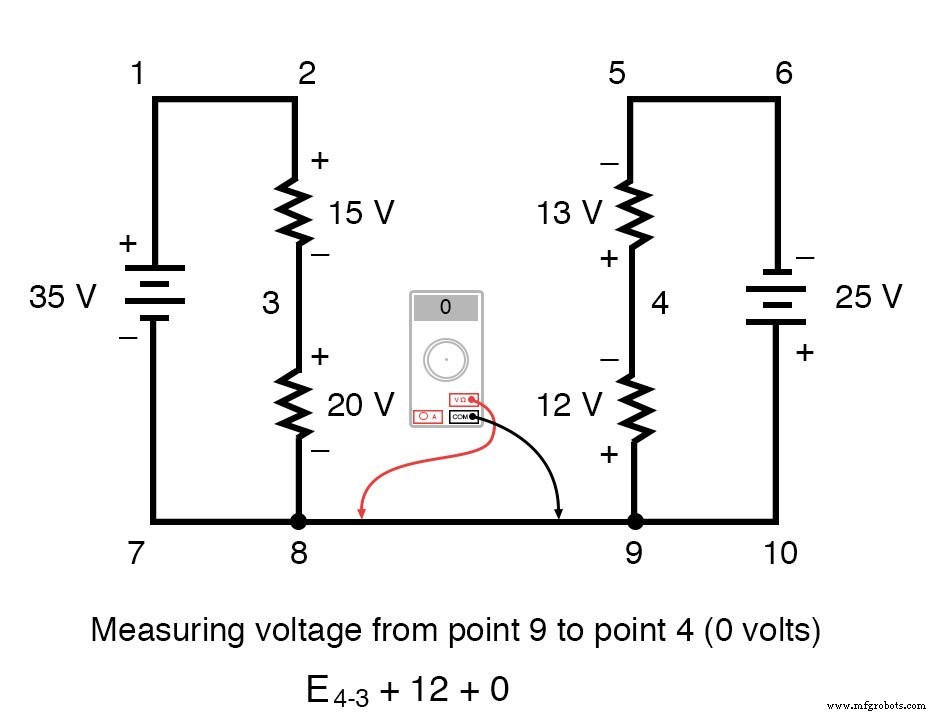
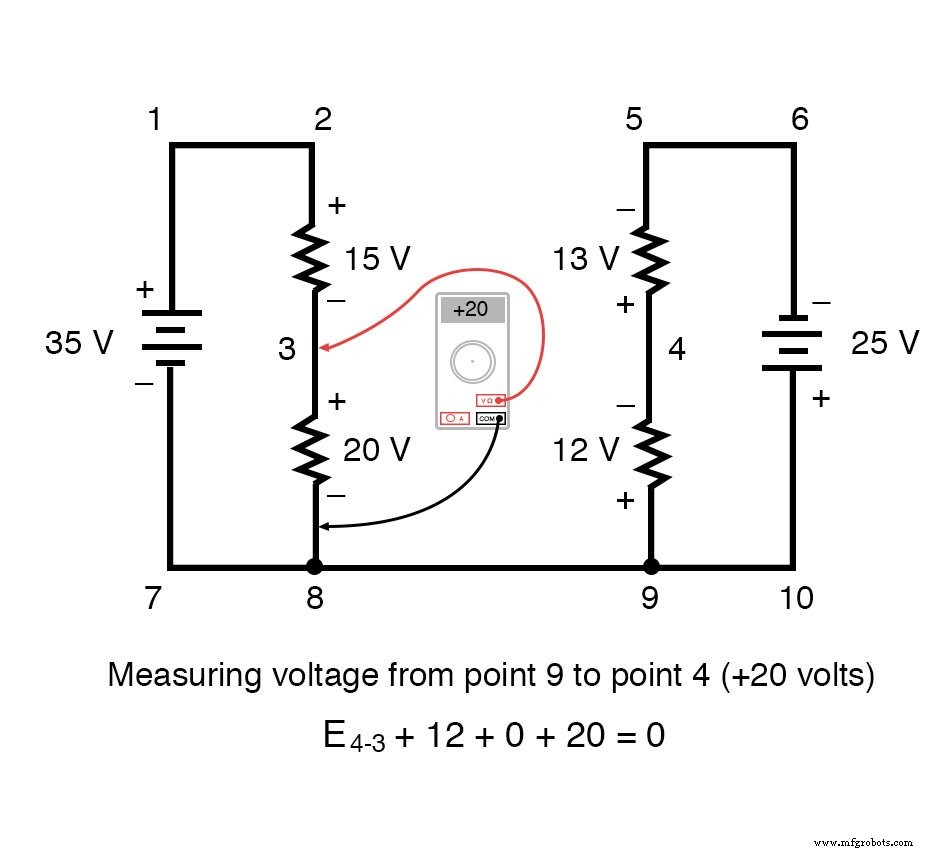
绕着循环 3-4-9-8-3，我们写下电压降数字，因为数字电压表会记录它们，随着我们前进，在前面的点上使用红色测试线，在后面的点上使用黑色测试线进行测量循环。因此，9点到4点的电压为正（+）12伏，因为“红线”在9点，“黑线”在4点。

从点 3 到点 8 的电压是正 (+) 20 伏，因为“红线”在点 3 上，“黑线”在点 8。当然，从点 8 到点 9 的电压为零，因为这两个点在电气上是公共的。

我们对从点 4 到点 3 的电压的最终答案是负 (-) 32 伏，告诉我们点 3 实际上相对于点 4 是正的，这正是数字电压表在点 4 上用红色引线指示的第 3 点的黑线：

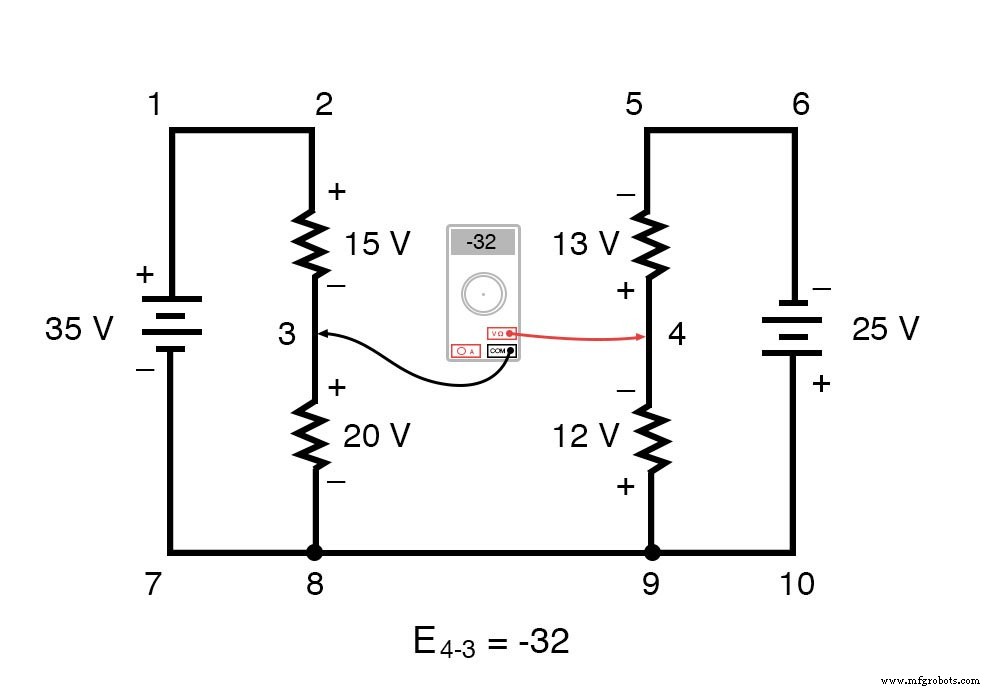
换句话说，在这个 KVL 问题中，我们的“仪表引线”的初始放置是“落后的”。如果我们生成了以 E3-4 而不是 E4-3 开始的 KVL 方程，以相反的仪表引线方向在同一循环中步进，最终答案将是 E3-4 =+32 伏：

重要的是要意识到这两种方法都不是“错误的”。在这两种情况下，我们都得出了对 3 和 4 两点之间电压的正确评估：点 3 相对于点 4 为正，它们之间的电压为 32 伏。

评论：

• 基尔霍夫电压定律 (KVL)：“回路中所有电压的代数和必须为零”

相关工作表：

• 基尔霍夫定律工作表