基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子

KCL 和 KVL - 基尔霍夫第一和第二定律与已求解示例

一位德国物理学家“罗伯特·基尔霍夫”在 1847 年引入了两个重要的电学定律，通过这些定律，我们可以很容易地找到复杂网络的等效电阻和不同导体中的流动电流。使用基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）这些简单的定律可以解决和简化交流和直流电路。

还要注意KCL是从电磁学中的电荷连续性方程推导出来的，而KVL是从静磁场的麦克斯韦-法拉第方程推导出来的（B对时间的导数为0 )。

基尔霍夫现行定律 (KCL)：

根据KCL：

在任何电网中，流入某一点的电流与从该点流出的电流的代数和为零。或者某一点的进入电流等于该点的离开电流。

换句话说，流向一个点的电流之和等于离开它的电流之和。或者说进入一个节点的电流的代数和等于离开它的电流的代数和。

KCL解释：

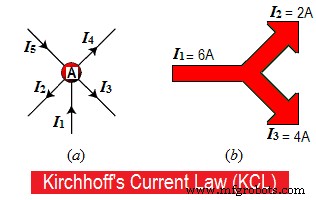
假设一些导体在“A”点相遇，如图 1.a 所示。在某些导体中，电流从“A”点流入，而在其他导体中，电流从“A”点流出或流出。

将流入或流入的电流视为“朝向“A”点的“正 (+)”，而从“A”点流出或流出的电流为“负 (-)”。
那么：

我 1 + (–我 2) + (–我 3) + (–我 4) + 我 5 =0

或

我 1 + 我 5 - 我 2 - 我 3 - 我 4 =0

或

我 1 + 我 5 =我 2 + 我 3 + 我 4 =0

即

流入或流入电流 =流出或流出电流

或者

Σ我 输入 =Σ我 离开

例如，图 1.b 中 8A 正朝着一个点而 5A 加 3A 离开该点，因此，

8A =5A + 3A

8A =8A.

基尔霍夫电压定律 (KVL)：

基尔霍夫第二定律或KVL指出；

换句话说，在任何闭环（也称为Mesh）中，施加的EMF的代数和等于元素中电压降的代数和.基尔霍夫第二定律也称为电压定律或网格定律。

ΣIR=ΣE

KVL解释：

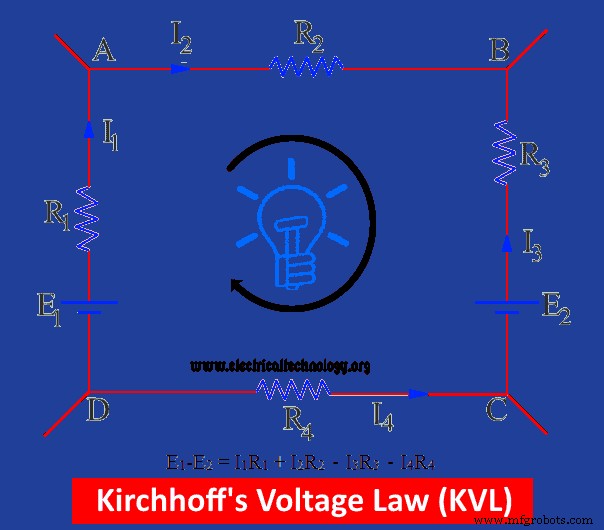
闭合电路如图所示，其中包含电池 E1 和 E2 的两个连接。电池 E.M.F 的总和由 E1-E2 表示。电流的假想方向也如图所示。

E1 以应该为正的方向驱动电流，而 E2 干扰电流的方向（即，它与假定的电流方向相反）因此，它被视为负数。这个闭合电路中的电压降取决于电压和电流的乘积。

在假定的电流方向上发生的电压降称为正电压降，另一个称为负电压降。

上图中，I1R1和I2R2为正压降，I3R3和I4R4为负V.D.

如果我们绕过闭合电路（或每个网格），并乘以导体的电阻和其中流动的电流，那么 IR 的总和等于连接到电路的应用 ​​EMF 源的总和。

上述电路的整体方程为：

E1 – E2 =i 1R1 + 我 2R2 - 我 3R3 - 我 4R4

如果我们按照图中所示的电流方向，那么IR的乘积为正，否则为负。

小知识：

电流方向：

通过基尔霍夫定律求解电路时，确定电流方向非常重要。与选举电流和常规电流的情况相同。

电流方向可以通过顺时针或逆时针方向来假设。一旦您选择了电流的自定义方向，您将不得不为整个电路应用并保持相同的方向，直到电路的最终解决方案。

如果我们得到的最终值是正数，这意味着电流的假定方向是正确的。如果为负值，则电流方向与当时的假设方向相反。

基尔霍夫定律的电路分析

关于 KCL 和 KVL（基尔霍夫定律）的求解示例

示例：

电阻 R1=10Ω、R2 =4Ω 和 R3 =8Ω 最多连接两节电池（电阻可忽略不计），如图所示。找出通过每个电阻的电流。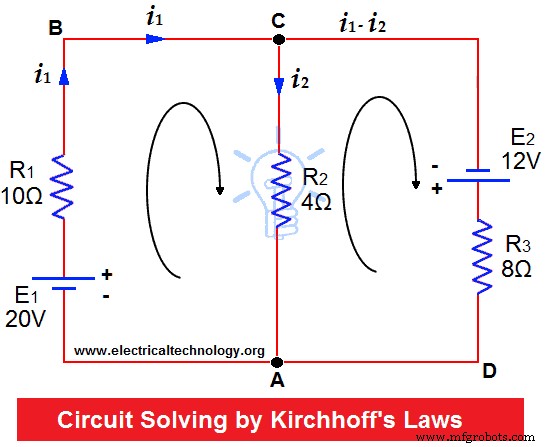

解决办法：

假设电流按箭头指示的方向流动。

在交汇点 C 和 A 上应用 KCL。

因此，当前网格 ABC =i 1

Current in Mesh CA =i 2

那么current in Mesh CDA =i 1 - 我 2

现在，在Mesh ABC上应用KVL，20V顺时针方向作用。等于IR乘积之和，得到；

10i 1 + 4我 2 =20  ...  (1)

在网状ACD中，12伏顺时针方向作用，则：

8(i 1 - 我 2) – 4我 2 =12

8i 1 - 8我 2 - 4我 2 =12

8i 1 - 12我 2 =12  ...  (2)

等式（1）乘以3；

30i 1 + 12我 2 =60

解决i 1

30i 1 + 12我 2 =60

8i 1 - 12我 2 =12

___________
38我 1 =72

上面的等式也可以用消去法或克莱默法则来简化。

i 1 =72 ÷ 38 =1.895 安培 =10 欧姆电阻中的电流

把这个值代入(1)中，我们得到：

10 (1.895) + 4i 2 =20

4i 2 =20 – 18.95

i 2 =0.263 安培 =4 欧姆电阻器中的电流。

现在，

i 1 – 我 2 =1.895 – 0.263 =1.632 安培

基尔霍夫定律的应用

• 基尔霍夫定律可用于确定电路中电流和电压等未知值的值以及这些五元组的流动方向。
• 这些定律可以应用于任何电路*（参见文末基尔霍夫定律的限制），但对于在复杂电路和网络中查找未知值很有用。
• 也用于节点和网格分析，以求电流和电压值。
• 通过每个独立回路的电流是通过应用KVL（每个回路）和通过计算所有电流（适用于回路电流法）在电路的任何元件中的电流来承载的。
• 通过每个分支的电流是通过在电路的每个回路中应用KCL（每个结）KVL来承载的（适用于回路电流法）。
• 基尔霍夫定律有助于理解通过电路的能量传输。

小知识：

在通过基尔霍夫定律简化和分析电路时必须考虑这些经验法则：

• 电流顺时针方向导致的回路电压降被认为是正（+）电压降。
• 电流逆时针方向导致的回路电压降被视为负 (-) 电压降。
• 电池顺时针方向导出的电流为正极（+）。
• 电池逆时针方向导出电流为正极（-）。

基尔霍夫定律的局限性：

• KCL 适用于电流仅在导体和电线中流动的假设。而在高频电路里，寄生电容就不能再忽略了。在这种情况下，电流可以在开路中流动，因为在这些情况下，导体或电线充当传输线。
• KVL 适用于假设没有波动的磁场连接闭环。然而，在高频但短波长的交流电路中存在变化的磁场时，电场不是保守的矢量场。因此，电场不可能是任何电位的梯度，并且环路周围电场的线积分不为零，这与 KVL 直接矛盾。这就是为什么 KVL 在这种情况下不适用的原因。
• 在将能量从磁场转移到电场期间，必须将软糖引入 KVL 以使电路周围的 P.d（电位差）等于 0。

电路分析定理相关文章：

• 戴维宁定理。一步一步的过程与解决的例子
• 诺顿定理。带示例的简单分步过程（图片视图）
• SUPERNODE 电路分析 |逐步解决示例
• SUPERMESH 电路分析 |逐步解决示例
• 交流和直流电路的最大功率传输定理
• 补偿定理——证明、解释和求解示例
• 替换定理 - 带求解示例的分步指南
• 米尔曼定理 - 分析交流和直流电路 - 示例
• 叠加定理 - 带求解示例的电路分析
• Tellegen 定理 - 求解示例和 MATLAB 仿真
• 分压器规则 (VDR) - R、L 和 C 电路的求解示例
• 电流分压器规则 (CDR) - 交流和直流电路的求解示例
• 欧姆定律：用语句和公式进行简单解释
• Star 到 Delta 和 Delta 到 Star 转换。 Y-Δ 变换