复数简介
如果我需要描述两个城市之间的距离,我可以提供一个由英里、公里或其他一些线性测量单位组成的单一数字的答案。
然而,如果我要描述如何从一个城市到另一个城市旅行,我必须提供更多的信息,而不仅仅是这两个城市之间的距离;我还必须提供有关方向的信息 也去旅行。
表示线性距离等单一维度的信息类型称为标量 数学中的数量。到目前为止,标量数是您在大多数数学应用程序中使用过的那种数字。
例如,电池产生的电压是一个标量。一根导线的电阻(欧姆)或通过它的电流(安培)也是如此。
然而,当我们开始分析交流电路时,我们发现电压、电流甚至电阻(称为阻抗 在交流中)不是我们习惯于在直流电路中测量的熟悉的一维量。
相反,这些量是动态的(方向和幅度交替),因此具有必须考虑的其他维度。频率和相移是其中两个起作用的维度。
即使在相对简单的交流电路中,我们只处理单一频率,除了幅度之外,我们仍然需要处理相移的维度。
为了成功地分析交流电路,我们需要使用能够表示这些多维量的数学对象和技术。
在这里,我们需要放弃标量数以换取更适合的东西:复数 .就像从一个城市到另一个城市给方向的例子一样,单频电路中的交流量既有幅度(类比:距离)也有相移(类比:方向)。
复数是能够同时表达幅度和相移这两个维度的单一数学量。
复数的图形表示
用图形表示复数时更容易掌握。如果我画一条具有特定长度(幅度)和角度(方向)的线,我就会得到一个复数的图形表示,这在物理学中通常称为 矢量 :(下图)
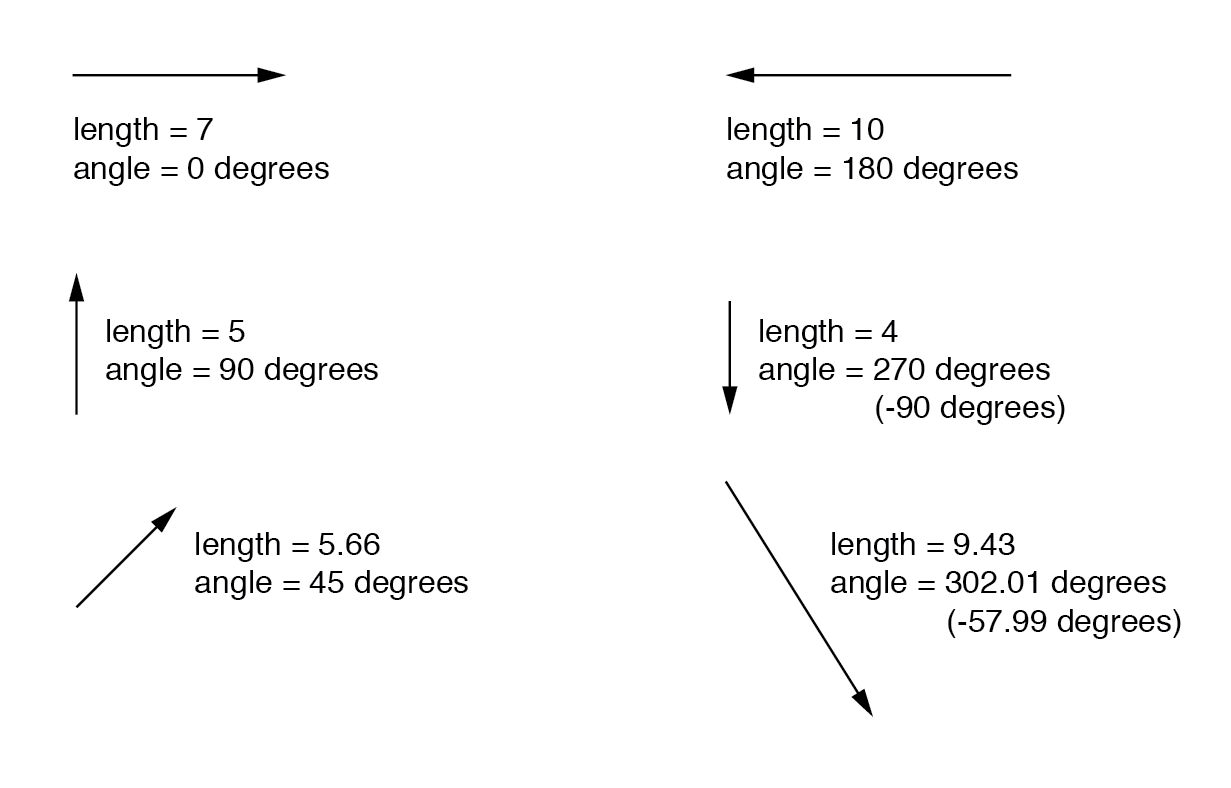
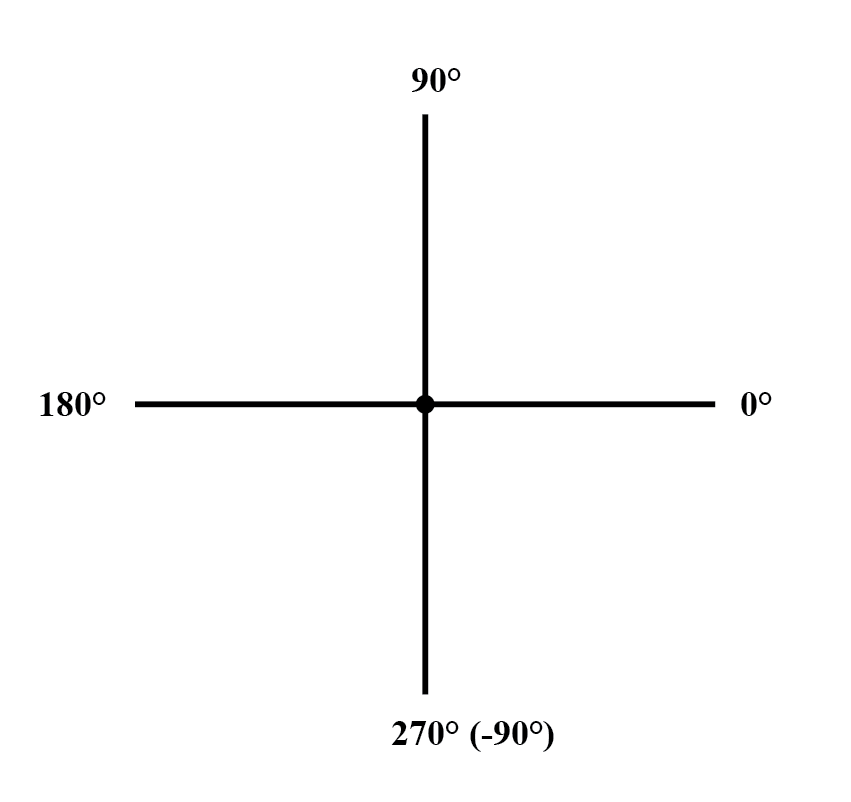
作为地图上的距离和方向,角度图形必须有一些共同的参考框架才能具有任何意义。在这种情况下,直接向右被认为是 0 o , 角度以逆时针方向为正方向计数:(下图)
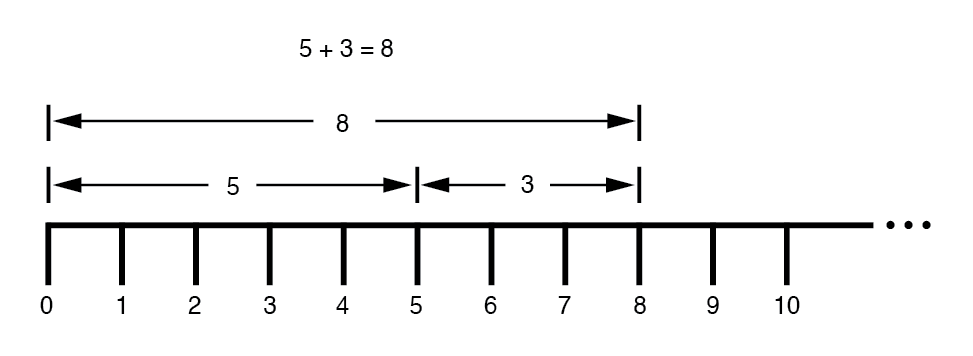
以图形形式表示数字的想法并不是什么新鲜事。这个我们小学的时候都是用“数轴”学的:(下图)

我们甚至通过查看长度(大小)如何叠加来给出最终答案,了解了加法和减法的工作原理:(下图)
后来,我们了解到有一些方法可以指定之间的值 线上标出的整数。这些是小数或小数:(下图)
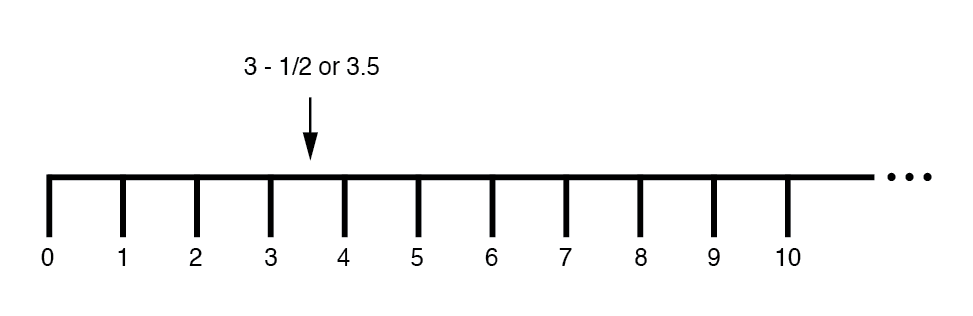
这些在小学学到的数域(整数、整数、有理数、无理数、实数等)有一个共同的特点:它们都是一维的 .数轴的直线度以图形方式说明了这一点。
您可以在数轴上上下移动,但沿该线的所有“运动”都仅限于单个轴(水平)。
一维标量数非常适合计算珠子、表示重量或测量直流电池电压,但它们无法表示更复杂的东西,例如距离和 两个城市之间的方向,或振幅和 交流波形的相位。
为了表示这些种类的数量,我们需要多维表示。换句话说,我们需要一条可以指向不同方向的数轴,而这正是向量。
评论:
- 一个标量 数字是人们在日常生活中习惯使用的数学对象类型:温度、长度、重量等一维量。
- 一个复数 是表示大小和方向两个维度的数学量。
- 一个向量 是复数的图形表示。它看起来像一个箭头,有起点、有尖端、有确定的长度和确定的方向。有时这个词 phasor 用于电气应用,其中矢量的角度表示波形之间的相移。
相关工作表:
- 交流阶段工作表
工业技术


