容差堆叠的最佳实践

公差叠加，也称为公差叠加，是指各种零件尺寸公差的组合。在零件的尺寸上确定公差后 ，重要的是测试该公差是否适用于工具的 公差：上限或下限。如果零件或组件的公差叠加不正确，则可能会出现不准确的情况。

公差的重要性

公差直接影响产品的成本和性能。更严格的公差使机加工零件更难制造，因此通常更昂贵。考虑到这一点，重要的是要在零件的可制造性、功能和成本之间找到平衡点。

成功公差堆叠的技巧

避免使用不必要的小公差

如上所述，更严格的公差会导致更高的制造成本，因为零件更难制造。这种较高的成本通常是由于发现尺寸超出公差时可能发生的报废零件数量增加。高质量刀柄和具有更严格公差的工具的成本也可能是额外的费用。

此外，不必要的小公差会导致更长的制造时间，因为需要更多的工作来确保零件在加工过程中以及在检查过程中加工后符合严格的标准。

小心不要过度标注零件

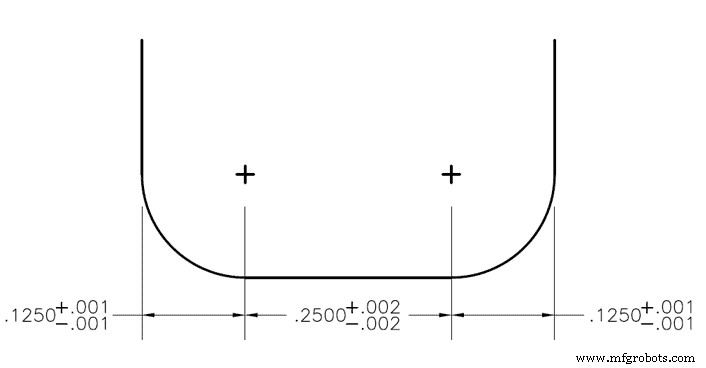
当零件的每个特征都标注了公差上限和下限时，尺寸过大可能会成为问题。例如，具有左右圆角半径的圆角半径立铣刀可能具有 +/- 0.001 英寸的公差，而它们之间的平面具有 0.002 英寸的公差。在这种情况下，刀具直径的公差窗口将是 +/- .004”，但在零件尺寸标注过程中经常会计算错误。此外，在此标注上设置公差会导致其尺寸过大，因此必须保留参考尺寸“REF”来代替公差。

利用统计容差分析：

基于标准偏差，统计分析着眼于所有三个公差低于或高于尺寸槽宽的可能性。该概率由正态概率密度函数表示，如下图 2 所示。通过结合设计中不同零件和尺寸的所有概率，我们可以根据零件的尺寸和公差确定零件出现问题或完全失效的概率。通常这种分析方法只用于具有四个或更多公差的装配体。

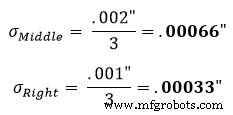
在开始统计公差分析之前，您必须计算或选择公差分布因子。标准分布为 3 。这意味着大多数数据（或在这种情况下的容差）将在平均值的 3 个标准差范围内。所有公差的标准偏差必须除以该公差分布因子，以将它们从 3 的分布标准化为 1 的分布。完成此操作后，就可以通过平方和求出装配的标准差。

可以把它想象成用 3 种不同大小的咖啡豆制成的一杯咖啡。为了制作一杯美味的咖啡，您必须首先将所有咖啡豆研磨成相同大小，以便将它们添加到咖啡过滤器中。在这种情况下，咖啡豆是标准偏差，研磨机是公差分布因子，咖啡过滤器是平方根方程。这是必要的，因为某些公差可能会根据公差范围的紧密程度而具有不同的分布因素。

如果要求槽必须为 0.500” 宽且公差为 +/- 0.003”，则使用统计分析方法，但不需要半径 (.125”) 和平面 (.250” ) 确切地说，只要它们适合插槽。在这个例子中，我们有 3 个双边公差，它们的标准偏差已经可用。由于它们是双边的，因此与平均值的标准偏差将只是 + 或 - 容差值。对于外半径，这将是 0.001 英寸，对于中间平坦区域，这将是 0.002 英寸。

对于这个例子，让我们使用等式1找到每个部分的标准偏差（σ）。在这个等式中表示标准偏差。

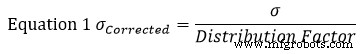
标准假设是零件公差代表 +/- 3 正态分布。因此，分布因子为3。利用图1左侧的等式1，我们发现其校正标准差等于：

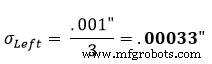
然后对中间和右侧部分重复此操作：

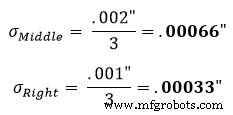
得出这些标准差后，我们将结果输入等式 2 以求出公差带的标准差。方程2称为和方根方程。

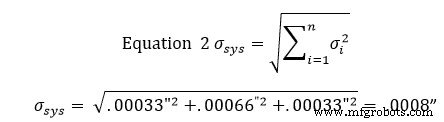
此时，这意味着 68% 的插槽将在 +/- .0008” 公差范围内。将此容差乘以 2 将得到 95% 的置信窗口，将其乘以 3 将得到 99% 的置信窗口。

68% 的插槽将在 +/- .0008 英寸内

95% 的插槽将在 +/- .0016 英寸范围内

99% 的插槽将在 +/- .0024 英寸范围内

这些置信度窗口是正态分布数据点集的标准。标准正态分布见上图2。

统计公差分析只能用于具有大于 4 个公差零件的装配体。在这个简单的分析中，很多因素都没有考虑到。此示例适用于 3 个双边尺寸，其公差代表它们与其平均值的标准偏差。在标准的统计公差分析中，角度、跳动、平行度等其他变量也会发挥作用，需要修正系数。

您是否知道 Harvey Performance Company 品牌与业界一流的凸轮软件供应商合作提供工具库？

点击这里了解更多

使用最坏情况分析：

最坏情况分析是将零件的所有公差相加以找到总零件公差的做法。执行此类分析时，每个公差都设置为其各自范围内的最大或最小限制。然后可以将这个总公差与零件的性能极限进行比较，以确保组件设计正确。这通常仅用于 1 个维度（仅 1 个平面，因此不涉及角度）和具有少量零件的装配体。

在为您的工作选择合适的切削工具时，也可以使用最坏情况分析，因为工具的公差可以添加到最坏情况下的零件公差中。一旦确定了这种情况，机械师或工程师就可以进行适当的调整，以使零件保持在打印上指定的尺寸范围内。应该注意的是，最坏的情况在实际生产中很少发生。虽然这些分析对于制造来说可能很昂贵，但它通过保证所有组件都能正常工作，让机械师放心。这种方法通常需要严格的公差，因为在最大条件下的总堆叠是设计中使用的主要特征。更严格的公差会增加制造成本，因为会增加刮削量、检查的生产时间以及用于这些零件的工具成本。

图 1 上下文中的最坏情况示例：

找出规格下限。

对于左角半径

.125” – .001” =.124”

平面部分

.250” – .002” =.248”

对于右角半径

.125” – .001” =.124”

将所有这些加到规格下限：

.124” + .248” + .124” =.496”

查找规格上限：

对于左角半径

.125” + .001” =.126”

平面部分

.250” + .002” =.252”

对于右角半径

.125” + .001” =.126”

将所有这些加到规格下限：

.126” + .252” + .126” =.504”

将两者相减并将此答案除以 2 以获得最坏情况容差：

（上限 - 下限）/2 =.004”

因此，此插槽的最坏情况是 0.500” +/- .004”。