电压和电流计算

有一种可靠的方法可以随时间计算无功直流电路中的任何值。

计算无功直流电路中的值

第一步是确定电容器或电感器反对变化的任何数量的起始值和最终值；也就是说，无论反应成分试图保持恒定的数量。对于电容器，这个量是电压;对于电感器，这个量是电流 .当电路中的开关闭合（或打开）时，无功分量将尝试将该量保持在与开关转换之前相同的水平，因此该值将用作“起始”值。

该数量的最终值是无限时间后该数量的任何值。这可以通过分析电容电路来确定，就像电容器是开路一样，而电感电路就像电感器是短路一样，因为这是这些组件达到“完全充电”时的行为，在无限长的时间之后。

下一步是计算时间常数 电路的：在瞬态情况下，电压或电流值从起始值到最终值变化约 63% 所需的时间。

在串联 RC 电路中，时间常数等于以欧姆为单位的总电阻乘以以法拉为单位的总电容。对于串联 L/R 电路，它是以亨利为单位的总电感除以以欧姆为单位的总电阻。无论哪种情况，时间常数都以秒为单位表示 并以希腊字母“tau”(τ) 表示：

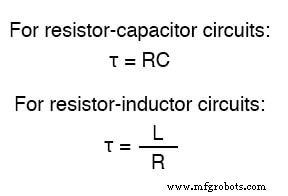
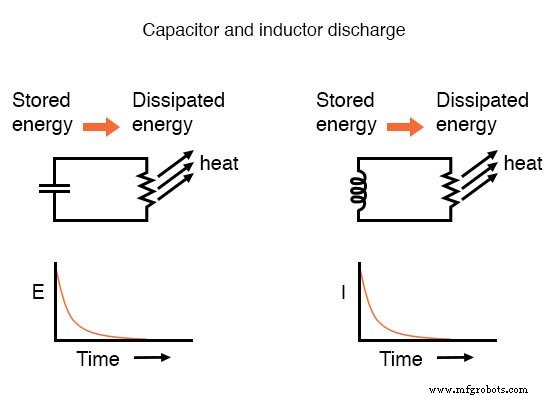
如前所述，响应瞬态的电压和电流等电路值的上升和下降渐近 .因此，这些值在瞬变后不久开始迅速变化并随着时间稳定下来。如果绘制在图形上，电压和电流的最终值的逼近形成指数曲线。

如前所述，一个时间常数是这些值中的任何一个从它们的起始值改变到它们的（最终）最终值大约 63% 所花费的时间。对于每个时间常数，这些值会（大约）向最终目标移动 63%。确定精确百分比的数学公式非常简单：

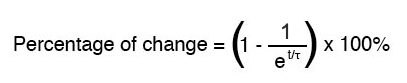
字母 e 代表欧拉常数，约为 2.7182818。它源自微积分技术，在对电路值的渐近方法进行数学分析之后。经过一个时间常数的时间后，从起始值到最终值的变化百分比为：

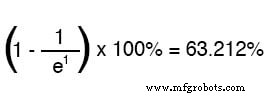
经过两个时间常数的时间，从起始值到最终值的变化百分比为：

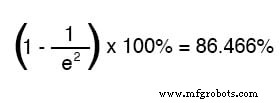
经过十个时间常数的时间后，百分比为：

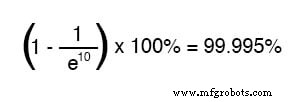
自电池瞬时施加电压以来经过的时间越长，分数中分母的值越大，这使得整个分数的值越小，这使得总计（1 减去分数）接近1，或 100%。

通用时间常数公式

我们可以从这个公式中得出一个更通用的公式来确定瞬态电路中的电压和电流值，方法是将此量乘以最终电路值和起始电路值之间的差值：

下面我们来分析一下本章开头所示的串联电阻电容电路的电压上升情况。

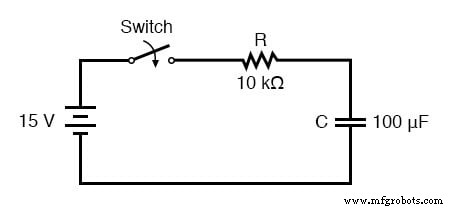
请注意，我们选择分析电压，因为这是电容器趋于保持恒定的数量。虽然该公式对电流很有效，但电流的起始值和最终值实际上是从电容器的电压得出的，因此计算电压是一种更直接的方法。电阻为 10 kΩ，电容为 100 µF（微法拉）。由于 RC 电路的时间常数 (τ) 是电阻和电容的乘积，我们得到的值为 1 秒：

如果电容器以完全放电状态（0 伏）开始，那么我们可以使用该电压值作为“启动”值。当然，最终值将是电池电压（15 伏）。我们这个电路中电容器电压的通用公式如下所示：

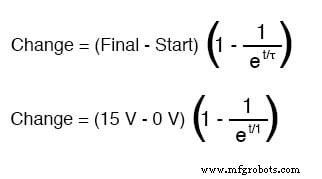
因此，在通过闭合开关施加电压 7.25 秒后，我们的电容器电压将增加：

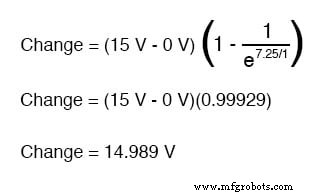
由于我们以 0 伏的电容器电压开始，因此 14.989 伏的增加意味着我们在 7.25 秒后有 14.989 伏。

相同的公式也可用于确定该电路中的电流。由于我们知道放电电容器最初的作用类似于短路，因此启动电流将是可能的最大值：15 伏（来自电池）除以 10 kΩ（开始时电路中唯一与电流相反的电压）：

我们还知道最终电流将为零，因为电容器最终将表现为开路，这意味着最终没有电子在电路中流动。现在我们知道了起始和最终电流值，我们可以使用我们的通用公式来确定同一 RC 电路中开关闭合 7.25 秒后的电流：

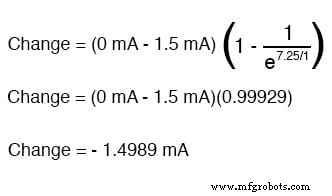
请注意，获得的变化数字是负数，而不是正数！这告诉我们电流已经减少 而不是随着时间的推移而增加。由于我们从 1.5 mA 的电流开始，这种下降 (-1.4989 mA) 意味着我们在 7.25 秒后有 0.001065 mA (1.065 µA)。

我们还可以通过从电池电压（15 伏）中减去电容器电压（14.989 伏）来确定 7.25 秒时的电路电流，以获得 10 kΩ 电阻器上的压降，然后计算通过电阻器的电流（以及整个串联电路）与欧姆定律（I =E / R）。无论哪种方式，我们都应该得到相同的答案：

使用通用时间常数公式分析电感电路

通用时间常数公式也适用于分析电感电路。让我们将其应用到本章开头的示例 L/R 电路中：

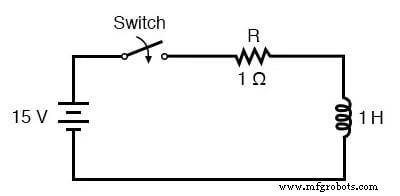
电感为 1 亨利，串联电阻为 1 Ω，我们的时间常数等于 1 秒：

因为这是一个电感电路，而且我们知道电感会阻止电流的变化，所以我们将为电流的起始值和最终值设置时间常数公式。如果我们从开关处于打开位置开始，电流将为零，因此零是我们的启动电流值。

开关长时间关闭后，电流将稳定到其最终值，等于电源电压除以总电路电阻 (I=E/R)，或者在此电路的情况下为 15 安培.

如果我们想确定 3.5 秒时的电流值，我们将应用通用时间常数公式如下：

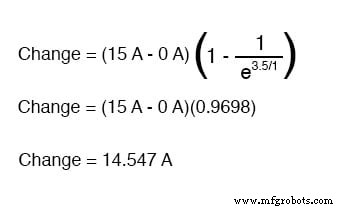
鉴于我们的启动电流为零，这使我们在 3.5 秒的时间内处于 14.547 安培的电路电流。

确定电感电路中的电压最好先计算电路电流，然后计算电阻上的电压降，找出电感上剩下的电压降。在我们的示例电路中只有一个电阻器（值为 1 Ω），这很容易：

从我们的 15 伏电池电压中减去，在时间 =3.5 秒时，电感器两端的电压为 0.453 伏。

评论：

• 通用时间常数公式：
• 要分析 RC 或 L/R 电路，请按以下步骤操作：
• (1)：确定电路的时间常数（RC 或 L/R）。
• (2)：确定要计算的量（其变化与电抗分量直接相反的任何量。对于电容器，这是电压；对于电感器，这是电流）。
• (3)：确定该数量的起始值和最终值。
• (4)：将所有这些值（最终、开始、时间、时间常数）代入通用时间常数公式并求解变化 数量上。
• (5)：如果起始值为零，则指定时间的实际值等于通用公式给出的计算变化。如果不是，请将更改添加到起始值以找出您所在的位置。

相关工作表：

• 时间常数电路工作表
• 时间常数计算工作表

查看我们的收藏 功率计算器 在我们的 工具 部分。