特性阻抗

无限长的平行线

不过，假设我们有一组无限的平行线 长度，末端没有灯。当我们关闭开关时会发生什么？由于电线末端不再有负载，因此该电路是开路的。会不会没有电流？ （下图）

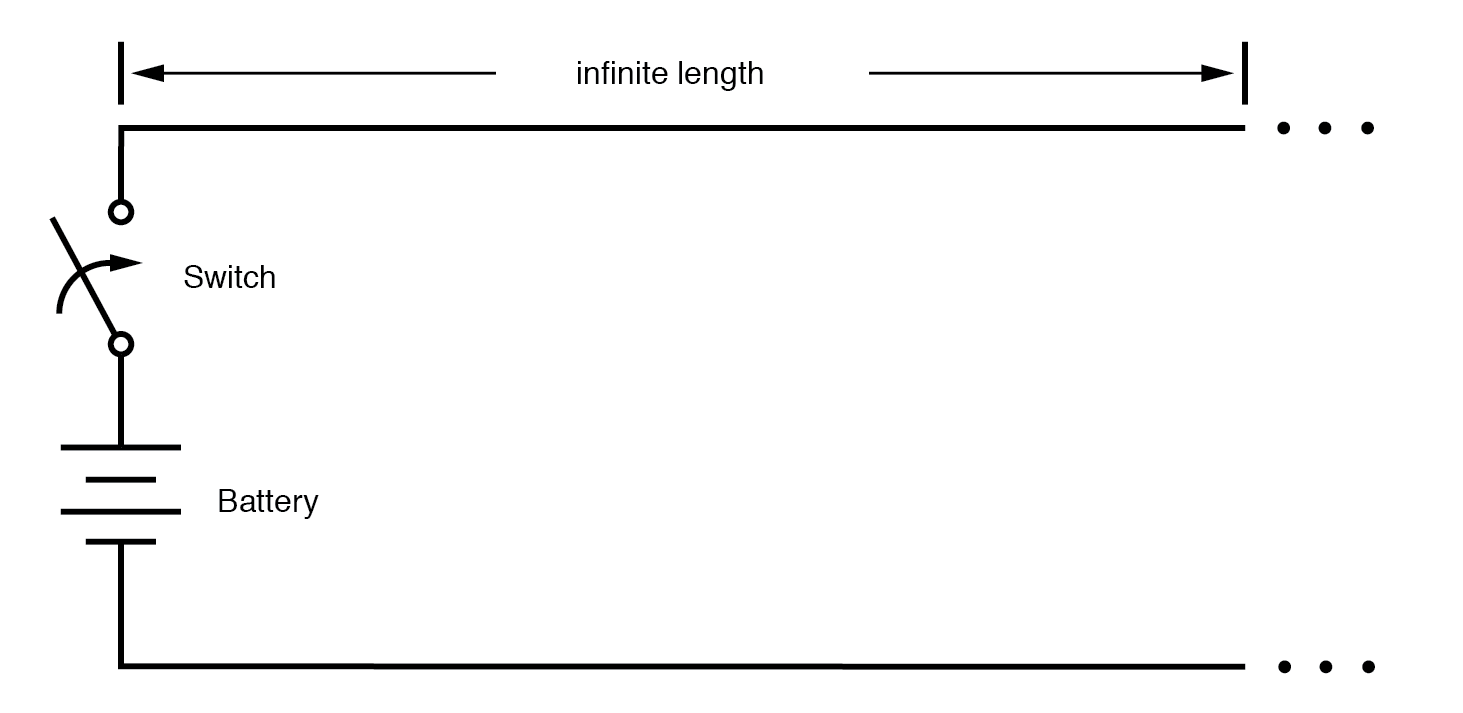
驱动无限传输线。

尽管在这个“思想实验”中可以通过使用超导体来避免导线电阻，但我们无法消除导线长度上的电容。 任何 由绝缘介质隔开的一对导体会在这些导体之间产生电容：（下图）

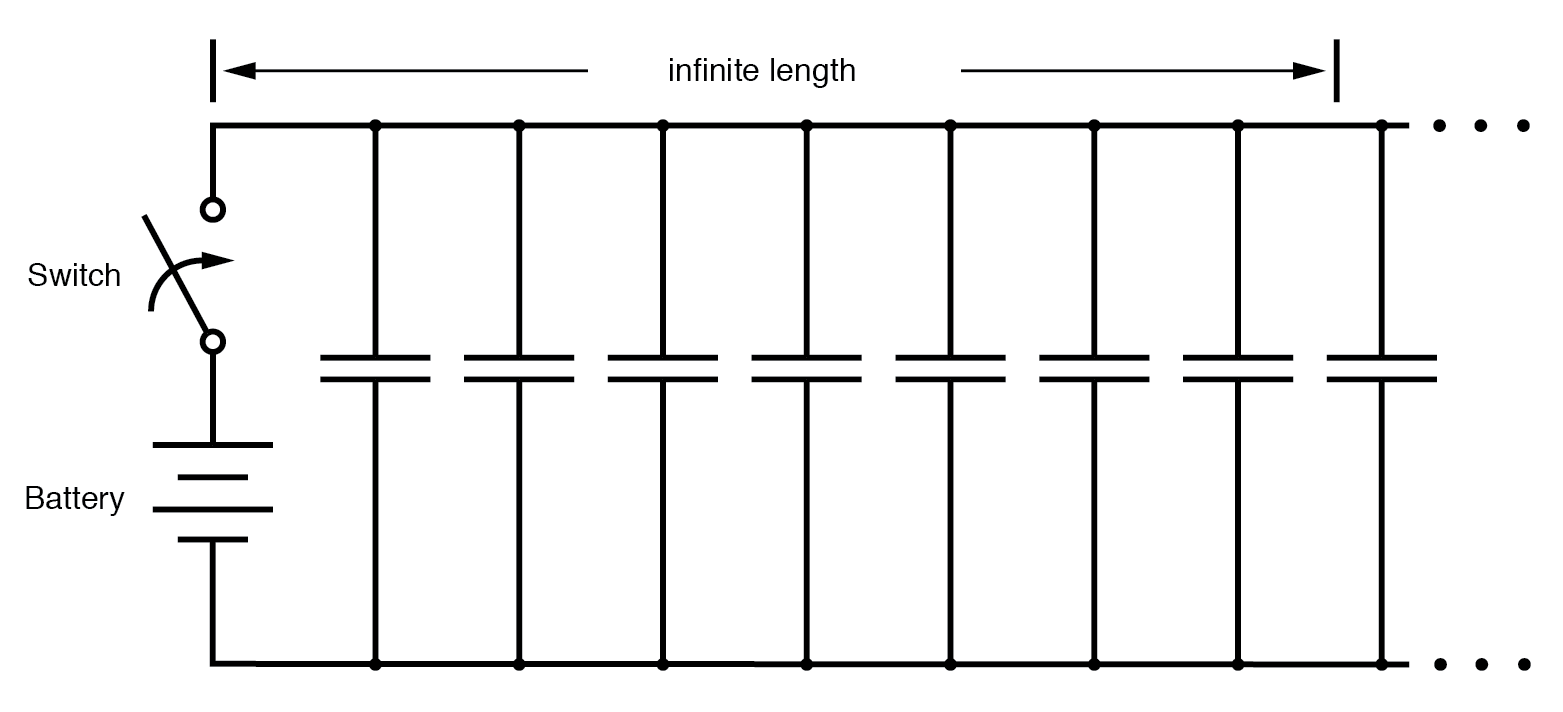
显示导体间杂散电容的等效电路。

施加在两个导体之间的电压会在这些导体之间产生电场。能量储存在这个电场中，这种能量储存会导致电压变化的反作用。电容对电压变化的反应由方程 i =C(de/dt) 描述，它告诉我们电流将与电压随时间的变化率成正比。因此，当开关闭合时，导体之间的电容将通过充电和从电源汲取电流来抵抗突然的电压升高。根据方程，施加电压的瞬间上升（由完美的开关闭合产生）会产生无限充电电流。

电容和电感

然而，一对平行导线所汲取的电流不会无限大，因为由于电感，沿导线存在一系列阻抗。 （下图）记住当前通过any 导体产生大小成正比的磁场。能量储存在这个磁场中，（下图），这种能量储存会导致电流的变化。每根导线在为导线之间的电容承载充电电流时都会产生磁场，并且这样做时会根据电感方程 e =L(di/dt) 降低电压。这种压降限制了分布电容两端的电压变化率，防止电流达到无限大：

显示杂散电容和电感的等效电路。

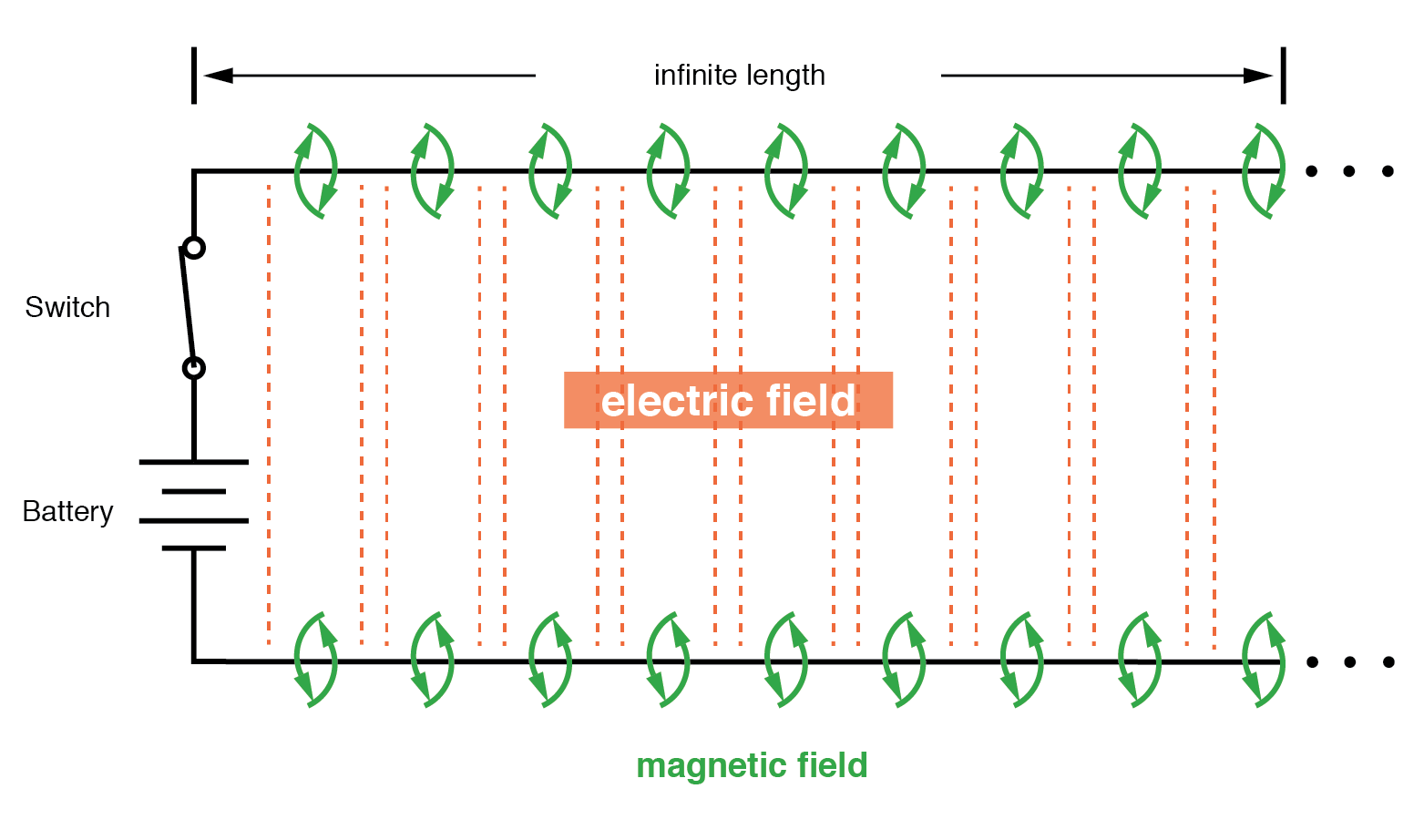
电压为电容充电，电流为电感充电。

由于两条导线中的电荷载流子以接近光速的速度相互传递运动，电压和电流变化的“波前”将以相同的速度沿导线的长度传播，导致分布电容和电感分别逐渐充电至满电压和满电流，如下所示：

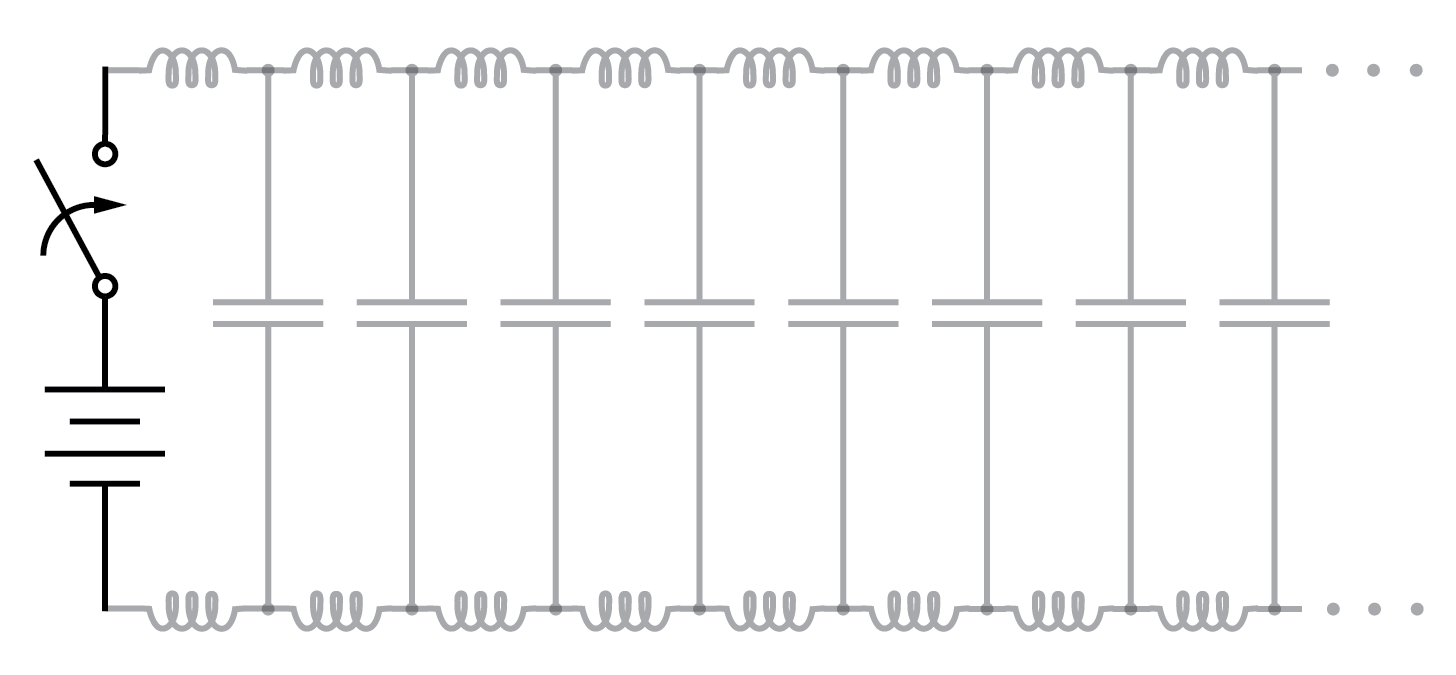
未充电传输线。

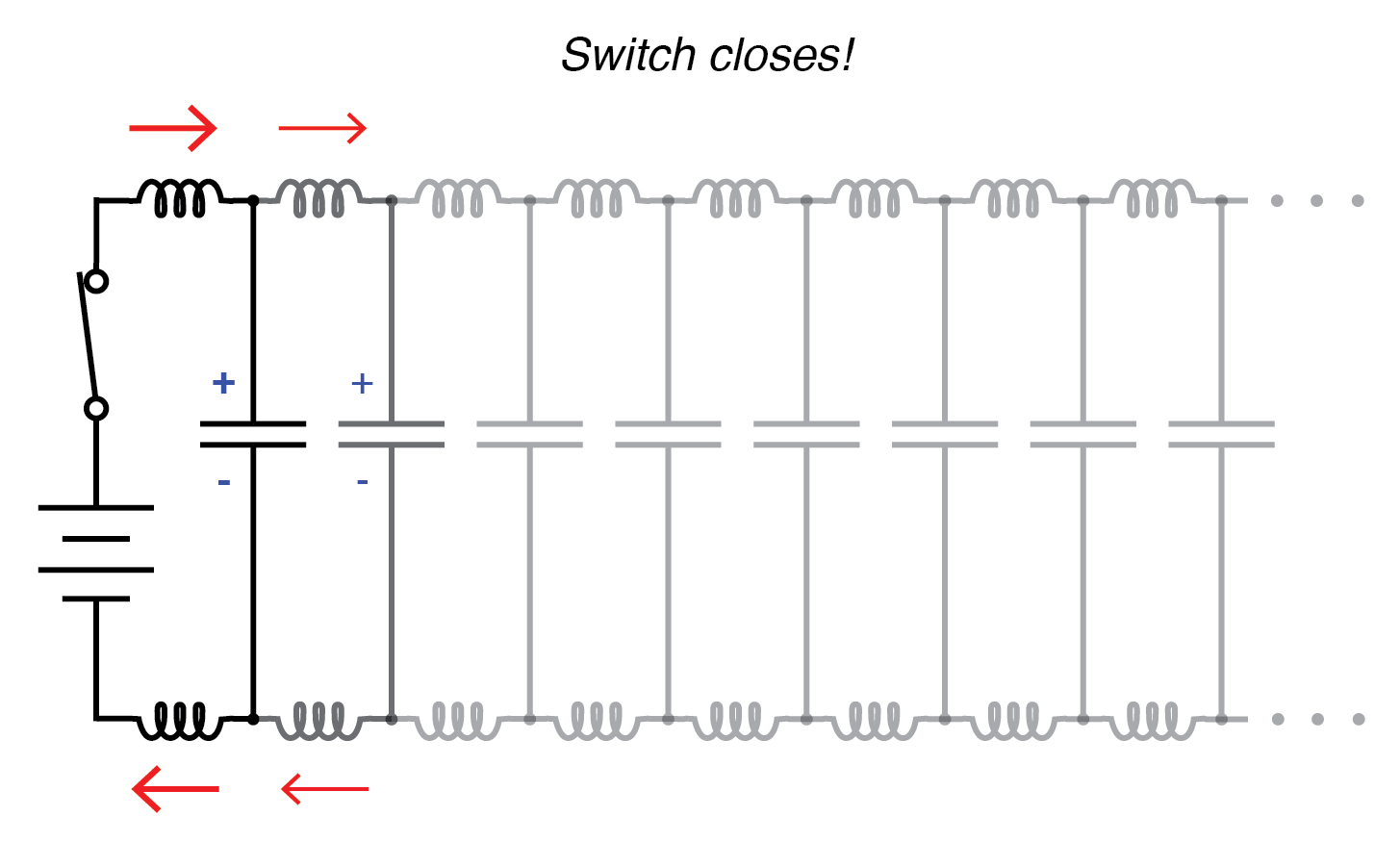
开始波传播。

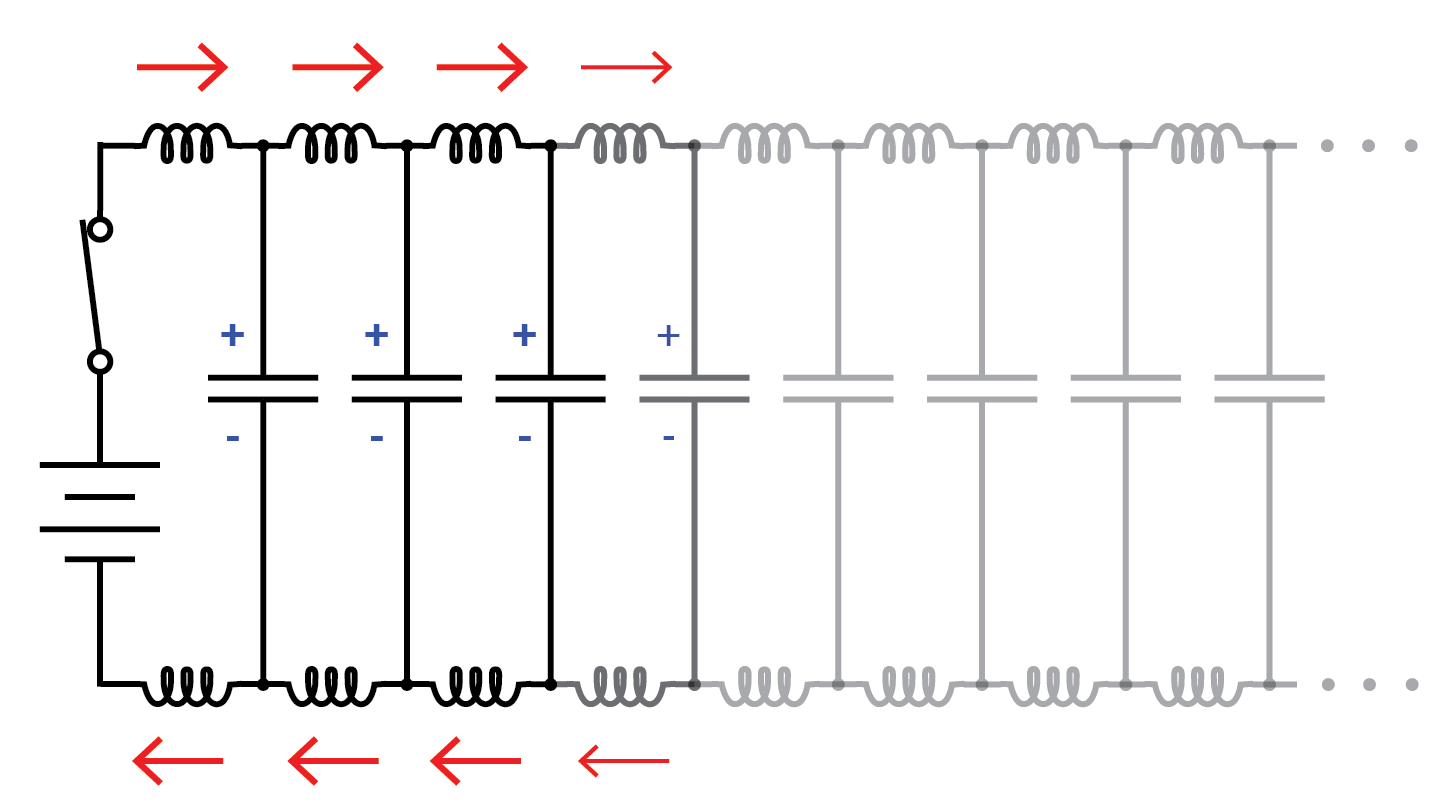
继续波传播。

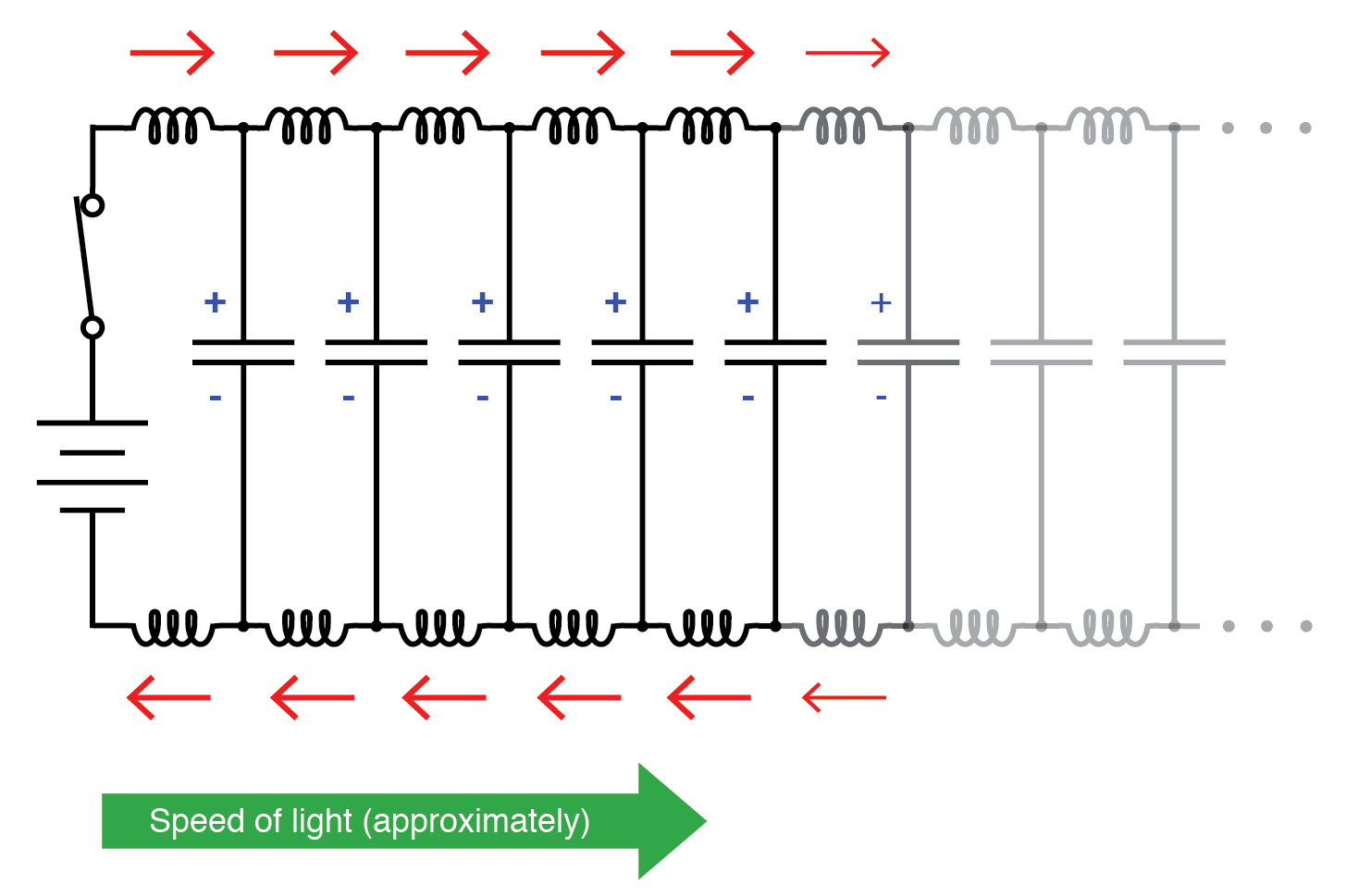
以光速传播。

传输线

这些相互作用的最终结果是通过电池电源的幅度有限的恒定电流。由于导线是无限长的，它们的分布电容永远不会完全充电到电源电压，它们的分布电感永远不会允许无限充电电流。换句话说，只要开关闭合，这对电线就会从电源汲取电流，表现为恒定负载。电线不再仅仅是电流的导体和电压的载体，现在它们本身就构成了一个具有独特特性的电路元件。两根电线不再只是一对导体 ，而是传输线 .

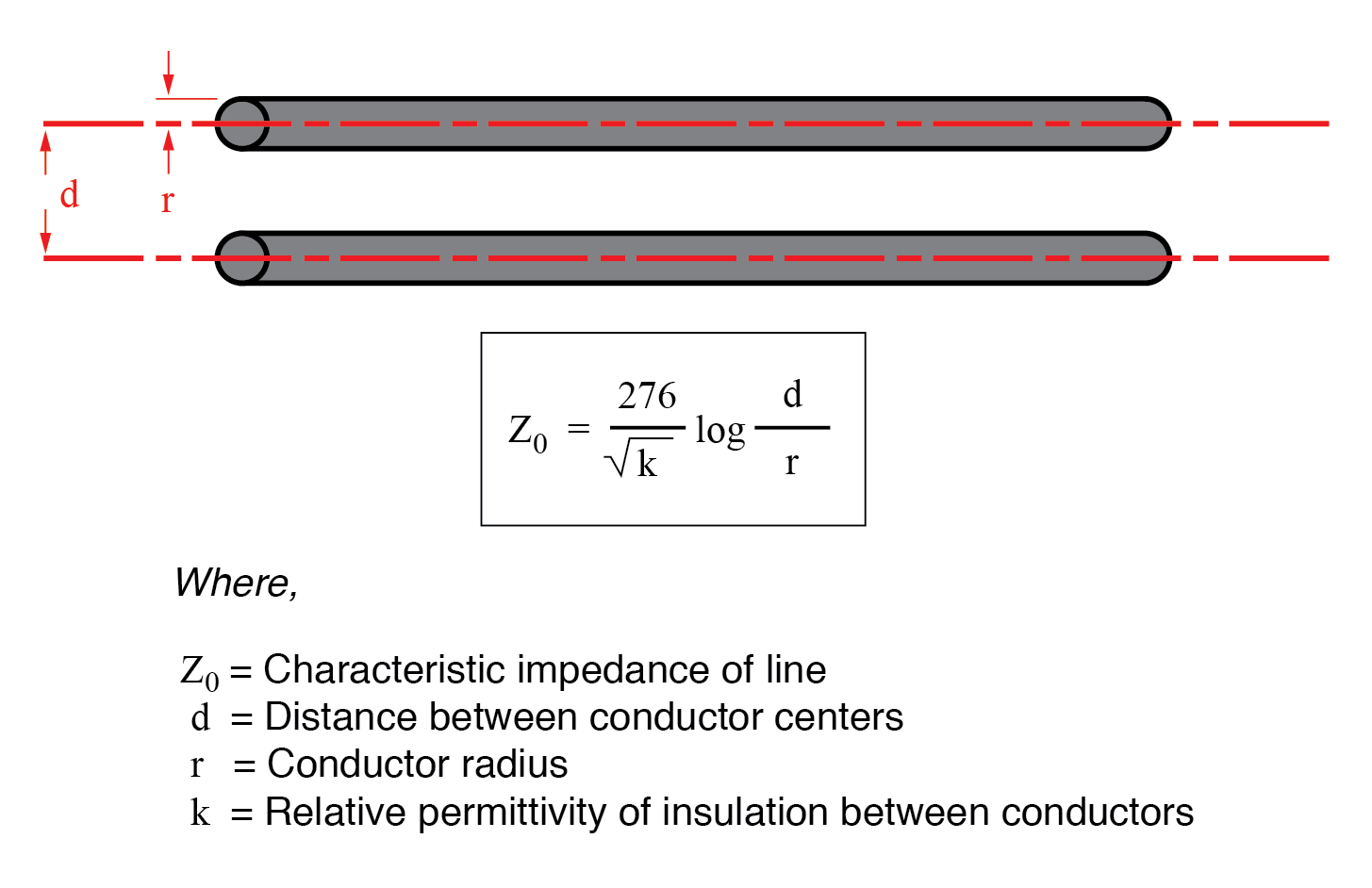
作为恒定负载，传输线对施加电压的响应是电阻性的而不是反应性的，尽管它完全由电感和电容组成（假设超导线的电阻为零）。我们可以这样说，因为从电池的角度来看，电阻永远耗散能量和无限传输线永远吸收能量没有区别。这条线以欧姆为单位的阻抗（电阻）称为特性阻抗 ，并且它由两个导体的几何形状固定。对于空气绝缘的平行线，特性阻抗可计算如下：

如果传输线在构造中是同轴的，则特征阻抗遵循不同的公式：

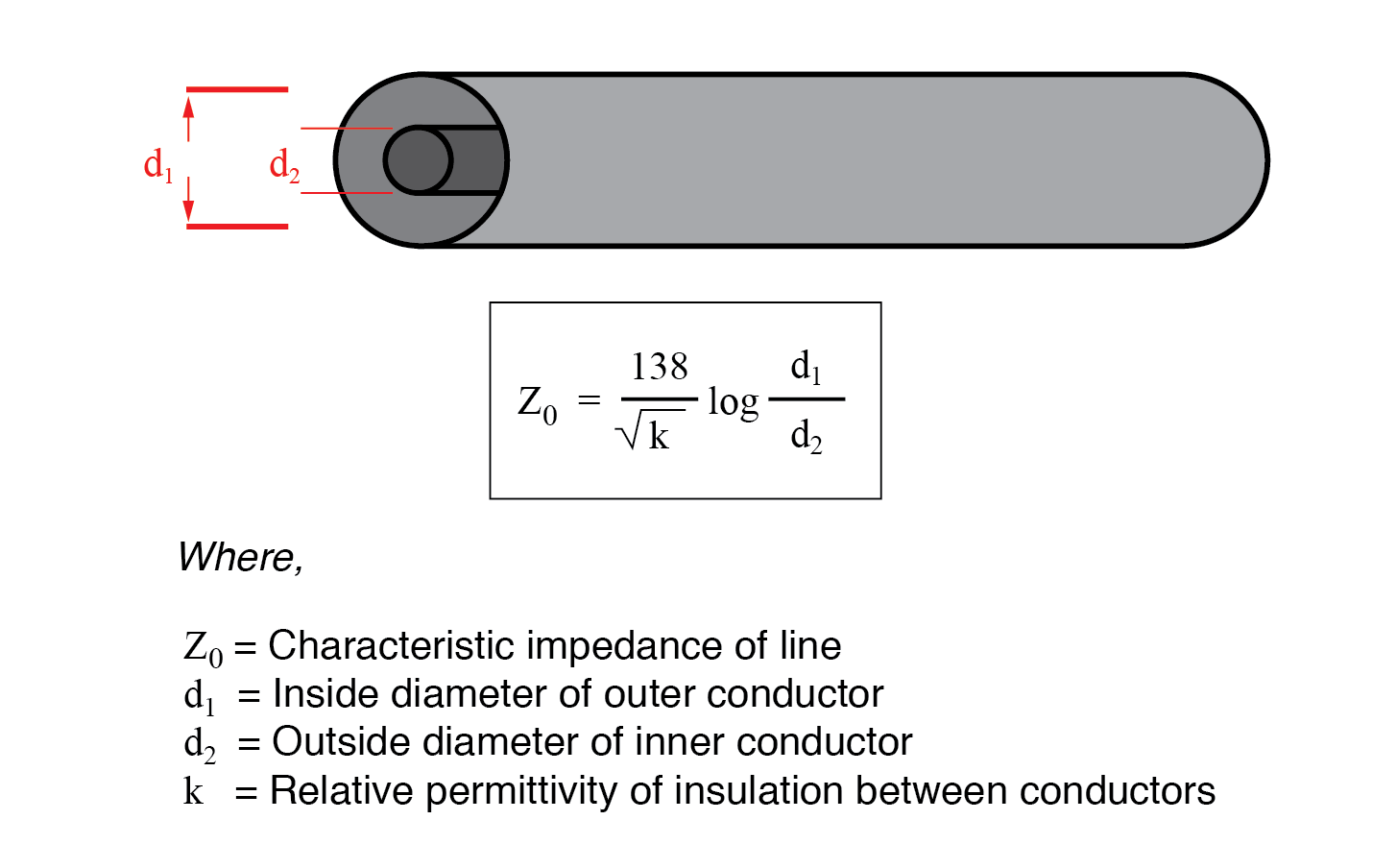
在这两个方程中，必须在两个分数项中使用相同的测量单位。如果绝缘材料不是空气（或真空），特性阻抗和传播速度都会受到影响。传输线的真实传播速度与真空中的光速之比称为速度因子 在那条线上。

速度因子纯粹是绝缘材料相对介电常数的一个因子（也称为介电常数 )，定义为材料的电场介电常数与纯真空的介电常数之比。任何电缆类型（同轴电缆或其他电缆）的速度因子都可以通过以下公式非常简单地计算：

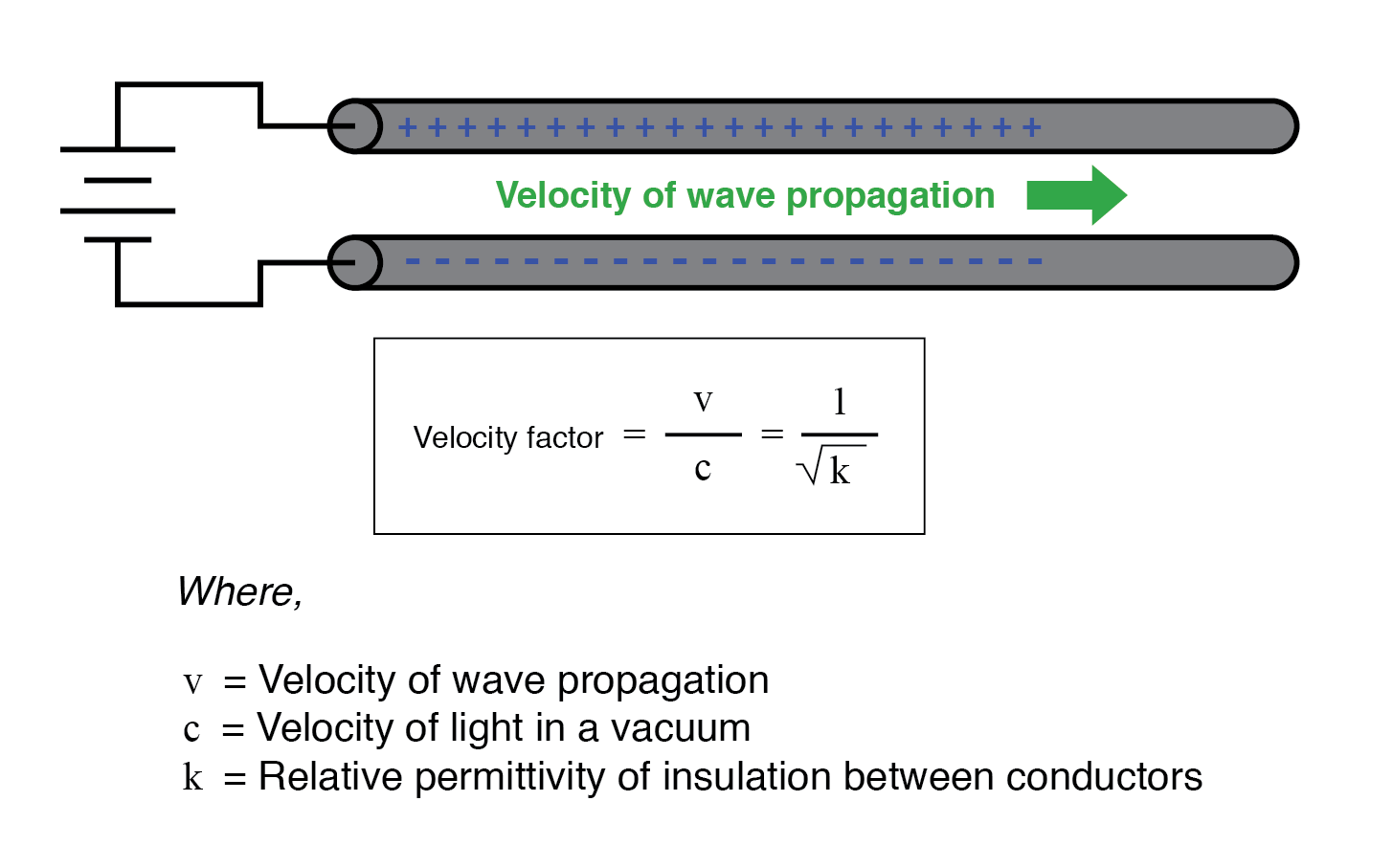
自然阻抗

特性阻抗也称为自然阻抗 ，并且它指的是无限长的传输线的等效电阻，这是由于分布电容和电感，因为电压和电流“波”沿其长度以等于光速的很大一部分的传播速度传播。

在前两个方程中的任何一个中都可以看出，传输线的特性阻抗 (Z0) 随着导体间距的增加而增加。如果导体彼此远离，分布电容将减小（电容器“板”之间的间距更大），并且分布电感将增加（两个相反磁场的抵消较少）。对于任何给定的施加电压量，较小的并联电容和较多的串联电感会导致线路汲取的电流较小，根据定义，这是更大的阻抗。相反，将两个导体靠得更近会增加并联电容并降低串联电感。对于给定的施加电压，这两种变化都会导致更大的电流消耗，相当于更小的阻抗。

除去介质“泄漏”和导体电阻等任何耗散效应，传输线的特征阻抗等于每单位长度线的电感除以每单位长度的线电容之比的平方根：

评论：

• 传输线 是一对平行导体，由于沿其长度分布电容和电感而表现出某些特性。
• 当电压突然施加到传输线的一端时，电压“波”和电流“波”都以接近光速沿传输线传播。
• 如果将直流电压施加到无限长传输线的一端，该线将从直流电源汲取电流，就好像它是一个恒定电阻。
• 特性阻抗 传输线的 (Z0) 是它在无限长时会表现出的电阻。这与分隔两个导体的电介质的漏电阻和导线本身的金属电阻完全不同。特性阻抗纯粹是沿线路长度分布的电容和电感的函数，即使电介质是完美的（无限并联电阻）和导线超导（零串联电阻）也会存在。
• 速度因子 是与传输线的传播速度与真空中的光速有关的分数。对于典型的两线制线路和同轴电缆，值范围在 0.66 和 0.80 之间。对于任何电缆类型，它都等于电缆绝缘的相对介电常数平方根的倒数 (1/x)。

相关工作表：

• 特性阻抗工作表