串联电阻-电容电路

在上一节中，我们了解了在简单的纯电阻和纯电容交流电路中会发生什么。现在我们将把这两个组件串联起来并研究其效果。

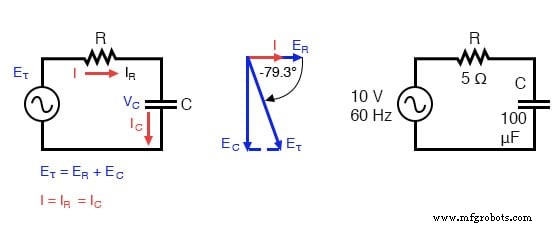
串联电容电路：电压滞后电流0°到90°。

阻抗计算

无论频率如何，电阻器都会对交流电流提供 5 Ω 的电阻，而电容器会在 60 Hz 时对交流电流提供 26.5258 Ω 的电抗。

因为电阻的阻值为实数（5Ω∠0°，或5+j0Ω），而电容的电抗是虚数（26.5258Ω∠-90°，或0-j26.5258Ω），综合效应两个分量的对立电流等于两个数的复数之和。

这种对电流的复杂反抗的术语是阻抗 ，其符号为Z，也以欧姆为单位表示，就像电阻和电抗一样。在上例中，总电路阻抗为：

正如您所料，阻抗与电压和电流有关，其方式类似于欧姆定律中的电阻：

事实上，这是一种比直流电子学 (E=IR) 中所教的欧姆定律更全面的形式，正如阻抗是一种比简单电阻更全面的反对电子流的表达方式。任何电阻和任何电抗，单独或组合（串联/并联），都可以并且应该表示为单个阻抗。

当前计算

要计算上述电路中的电流，我们首先需要为电压源提供一个相角参考，一般假定为零。 （阻性阻抗和容性阻抗的相角总是 分别为 0° 和 -90°，与给定的电压或电流相角无关。）

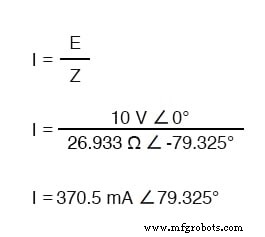
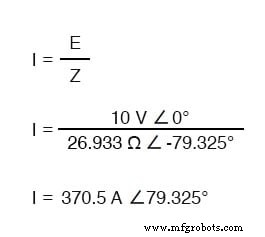
与纯电容电路一样，电流波领先于（源）电压波，尽管这次差异是 79.325°，而不是完整的 90°。

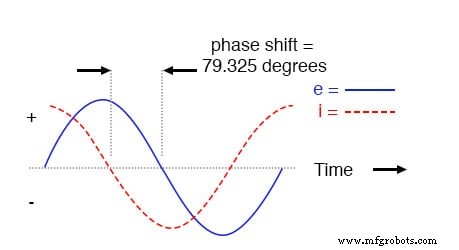
串联 R-C 电路中的电压滞后于电流（电流超前电压）。

表法

正如我们在交流电感一章中学到的，组织电路数量的“表格”方法是交流分析的一个非常有用的工具，就像它用于直流分析一样。让我们将这个串联电路的已知数字列在一个表格中，然后使用这个工具继续分析：

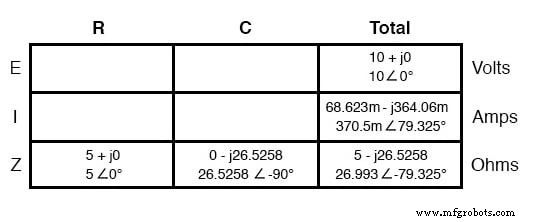
串联电路中的电流由所有组件平均分配，因此放置在电流“总计”列中的数字也可以分配到所有其他列：

继续我们的分析，我们可以垂直应用欧姆定律 (E=IR) 来确定电阻器和电容器两端的电压：

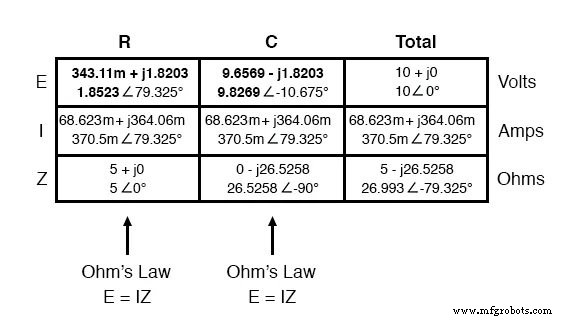
请注意电阻器两端的电压如何与通过它的电流具有完全相同的相位角，这告诉我们 E 和 I 同相（仅适用于电阻器）。电容器两端的电压相角为 -10.675°，正好小于 90° 大于电路电流的相角。这告诉我们电容器的电压和电流仍然彼此相差 90°。

使用 SPICE 进行计算

让我们用 SPICE 检查我们的计算：

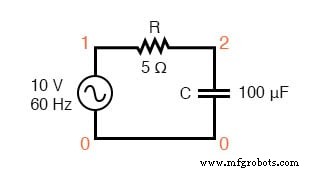
Spice 电路：R-C。

ac r-c 电路 v1 1 0 交流 10 罪 r1 1 2 5 c1 2 0 100u .ac 林 1 60 60 .print ac v(1,2) v(2,0) i(v1) .print ac vp(1,2) vp(2,0) ip(v1) 。结尾 频率 v(1,2) v(2) i(v1) 6.000E+01 1.852E+00 9.827E+00 3.705E-01 频率 vp(1,2) vp(2) ip(v1) 6.000E+01 7.933E+01 -1.067E+01 -1.007E+02 

再一次，SPICE 令人困惑地以等于实际相位角加 180°（或负 180°）的值打印当前相位角。

但是，纠正这个数字并检查我们的工作是否正确是一件简单的事情。在这种情况下，SPICE 输出的电流相位角 -100.7° 等于正 79.3°，这与我们之前计算的数字 79.325° 相对应。

再次强调，与实际电压和电流测量值相对应的计算数字是极性 形式，不是矩形形式！

例如，如果我们实际构建这个串联电阻-电容电路并测量电阻两端的电压，我们的电压表将显示 1.8523 伏特，不是 343.11 毫伏（真正的矩形）或 1.8203 伏（假想的矩形）。

连接到真实电路的真实仪器提供与计算数字的矢量长度（幅度）相对应的指示。虽然复数符号的矩形形式对于执行加减法很有用，但它是一种比极坐标更抽象的符号形式，仅与真实测量值直接对应。

给定电阻 (R) 和容抗 (XC)，可以计算串联 R-C 电路的阻抗 (Z)。由于 E=IR、E=IXC 和 E=IZ，电阻、电抗和阻抗分别与电压成正比。因此，电压相量图可以用类似的阻抗图代替。

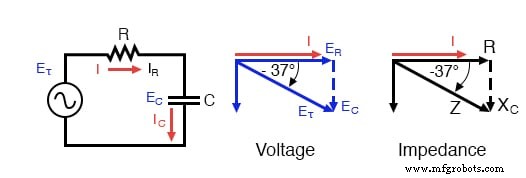
系列：R-C 电路阻抗相量图。

示例： 给定：一个 40 Ω 电阻器与一个 88.42 微法拉电容器串联。求出 60 赫兹处的阻抗。

 XC =1/(2πfC) XC =1/(2π·60·88.42×10-6) XC =30 Ω Z =R - jXC Z =40 - j30 |Z| =sqrt(402 + (-30)2) =50 Ω ∠Z =反正切（-30/40）=-36.87° Z =40 - j30 =50∠-36.87° 

评论：

• 阻抗 是对抗电流的总度量，是（“实”）电阻和（“虚”）电抗的复（矢量）和。
• 阻抗 (Z) 的管理就像串联电路分析中的电阻 (R) 一样：串联阻抗相加形成总阻抗。请务必以复杂（非标量）形式执行所有计算！ ZTotal1 + Z2 + 。 . .锌
• 请注意，阻抗总是串联相加，无论构成阻抗的组件是什么类型。也就是说，电阻阻抗、电感阻抗和电容阻抗在数学上的处理方式相同。
• 纯电阻阻抗的相位角始终为 0°（ZR =R Ω ∠ 0°）。
• 纯电容性阻抗的相位角始终为 -90°（ZC =XC Ω ∠ -90°）。
• 交流电路的欧姆定律：E =IZ； I =E/Z; Z =E/I
• 当电阻器和电容器在电路中混合在一起时，总阻抗的相位角将介于 0° 和 -90° 之间。

相关工作表：

• 串联和并联交流电路工作表