如何在 Python 中创建多层感知器神经网络
本文将带您逐步了解一个 Python 程序,该程序将使我们能够训练神经网络并执行高级分类。
这是 AAC 神经网络开发系列的第 12 篇文章。在下面查看该系列还提供什么:
- 如何使用神经网络进行分类:什么是感知器?
- 如何使用简单的感知器神经网络示例对数据进行分类
- 如何训练基本的感知器神经网络
- 了解简单的神经网络训练
- 神经网络训练理论简介
- 了解神经网络中的学习率
- 使用多层感知器进行高级机器学习
- Sigmoid 激活函数:多层感知器神经网络中的激活
- 如何训练多层感知器神经网络
- 了解多层感知器的训练公式和反向传播
- Python 实现的神经网络架构
- 如何在 Python 中创建多层感知器神经网络
- 使用神经网络进行信号处理:神经网络设计中的验证
- 训练神经网络数据集:如何训练和验证 Python 神经网络
在本文中,我们将利用我们在感知器神经网络上所做的工作,并学习如何用熟悉的语言实现一个:Python。
为神经网络开发易于理解的 Python 代码
最近我查看了很多关于神经网络的在线资源,尽管那里无疑有很多很好的信息,但我对我发现的软件实现并不满意。它们总是太复杂、太密集或不够直观。在我编写 Python 神经网络时,我真的很想做出一些可以帮助人们了解系统运作方式以及神经网络理论如何转化为程序指令的东西。
但是,有时代码的清晰性和代码的效率是成反比的。我们将在本文中讨论的程序绝对不是 针对快速性能进行了优化。优化是神经网络领域内的一个严重问题;现实生活中的应用程序可能需要大量的培训,因此彻底的优化可以显着减少处理时间。然而,对于像我们将要做的那些简单的实验,训练不会花费很长时间,而且没有理由强调强调简单性和理解性而不是速度的编码实践。
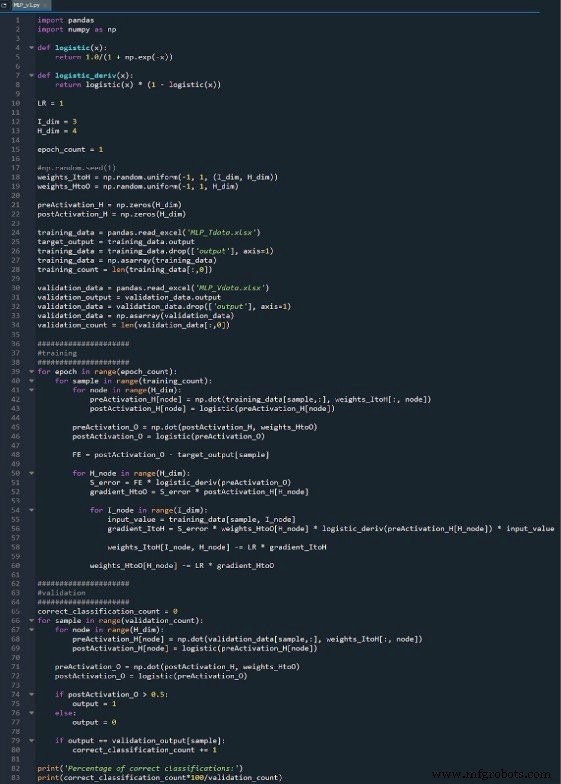
整个 Python 程序作为图像包含在本文末尾,文件(“MLP_v1.py”)作为下载提供。代码执行训练和验证;本文侧重于训练,稍后我们将讨论验证。但是,无论如何,验证部分中没有多少功能未包含在训练部分中。
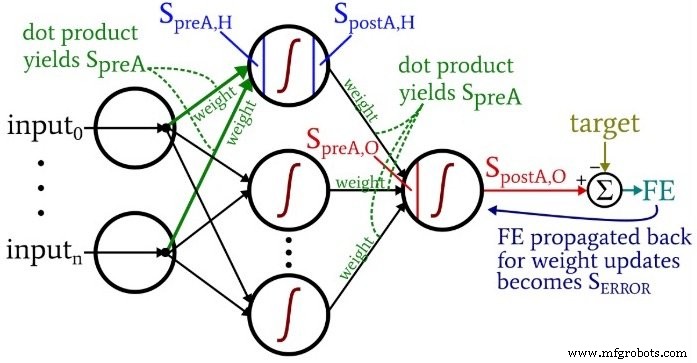
在您思考代码时,您可能想回顾一下我在第 10 部分中提供的略显繁琐但信息量丰富的架构加术语图。
准备函数和变量
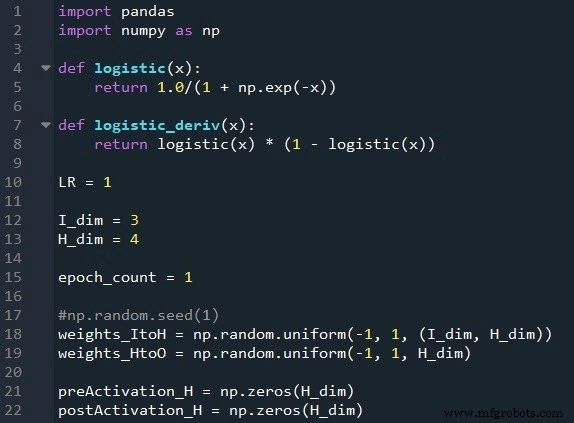
NumPy 库广泛用于网络计算,Pandas 库为我提供了一种从 Excel 文件导入训练数据的便捷方法。
如您所知,我们使用逻辑 sigmoid 函数进行激活。计算激活后值需要logistic函数本身,反向传播需要logistic函数的导数。
接下来我们选择学习率、输入层的维数、隐藏层的维数和历元数。多个时期的训练对于真实的神经网络很重要,因为它允许您从训练数据中提取更多的学习。在 Excel 中生成训练数据时,您无需运行多个 epoch,因为您可以轻松创建更多训练样本。
np.random.uniform() 函数用 –1 和 +1 之间的随机值填充我们的两个权重矩阵。 (注意隐藏到输出矩阵实际上只是一个数组,因为我们只有一个输出节点。)np.random.seed(1) 语句导致每次运行程序时随机值都相同。初始权重值会对训练后的网络的最终性能产生显着影响,因此如果您尝试评估 other 变量提高或降低性能,您可以取消注释该指令,从而消除随机权重初始化的影响。
最后,我为隐藏层中的 preactivation 和 postactivation 值创建空数组。
导入训练数据

这与我在第 4 部分中使用的过程相同。我从 Excel 导入训练数据,分离出“输出”列中的目标值,删除“输出”列,将训练数据转换为 NumPy 矩阵,并存储training_count 中的训练样本数 变量。
前馈处理
产生输出值的计算以及数据在典型神经网络图中从左向右移动的计算构成了系统操作的“前馈”部分。这是前馈代码:
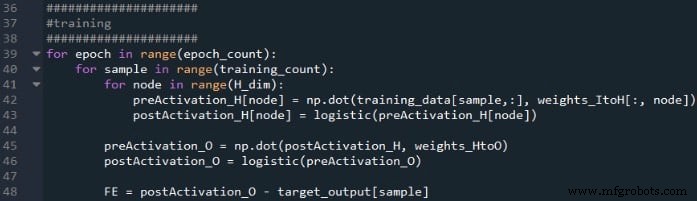
第一个 for 循环允许我们有多个 epoch。在每个时期内,我们为每个样本计算一个输出值(即输出节点的激活后信号),并且逐个样本的操作被第二个 for 循环捕获。在第三个 for 循环中,我们单独关注每个隐藏节点,使用点积生成预激活信号,使用激活函数生成激活后信号。
之后,我们准备计算输出节点的预激活信号(再次使用点积),我们应用激活函数来生成激活后信号。然后我们从输出节点的激活后信号中减去目标以计算最终误差。
反向传播
在我们执行了前馈计算之后,是时候反转方向了。在程序的反向传播部分,我们从输出节点移向隐藏到输出的权重,然后是输入到隐藏的权重,带来了我们用来有效训练网络的错误信息。

我们在这里有两层 for 循环:一层用于隐藏到输出的权重,一层用于输入到隐藏的权重。我们首先生成SERROR,我们需要它来计算gradientHtoO和gradientItoH,然后我们通过减去乘以学习率的梯度来更新权重。
注意输入到隐藏的权重如何更新 隐藏到输出循环。我们从导致返回隐藏节点之一的错误信号开始,然后我们将该错误信号扩展到连接到这个隐藏节点的所有输入节点:
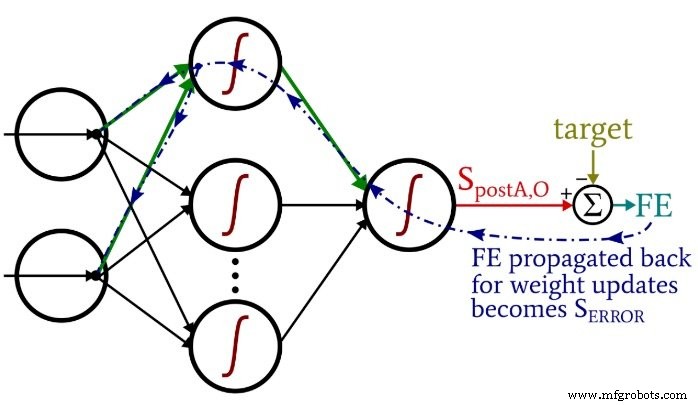
在与该隐藏节点关联的所有权重(包括 ItoH 和 HtoO)都已更新后,我们返回并从下一个隐藏节点重新开始。
另请注意,在 HtoO 权重之前修改了 ItoH 权重。我们在计算gradientItoH时使用当前的HtoO权重,因此我们不想在执行此计算之前更改HtoO权重。
结论
想想在这个相对较短的 Python 程序中融入了多少理论是很有趣的。我希望这段代码能帮助您真正理解我们如何在软件中实现多层感知器神经网络。
你可以在下面找到我的完整代码:
下载代码
工业机器人


