了解神经网络训练中的局部最小值

本文讨论了一个复杂的问题，它会阻止您的感知器达到足够的分类准确度。

在 AAC 神经网络系列中，我们涵盖了与理解和开发多层感知器神经网络相关的广泛主题。在阅读有关局部最小值的这篇文章之前，请先了解以下系列的其余部分：

神经网络训练是一个复杂的过程。幸运的是，我们不必完全理解它就可以从中受益：我们使用的网络架构和训练程序确实产生了实现非常高分类精度的功能系统。然而，培训的一个理论方面尽管有些深奥，但值得我们关注。

我们将其称为“局部最小值问题”。

嗯……我不确定。当我第一次了解神经网络时，我的印象是局部最小值确实是成功训练的一个重大障碍，至少在我们处理复杂的输入-输出关系时是这样。然而，我相信最近的研究淡化了局部最小值的重要性。也许更新的网络结构和处理技术减轻了问题的严重性，或者我们只是更好地理解了神经网络如何实际导航到所需的解决方案。

我们将在本文末尾重新审视局部最小值的当前状态。现在，我将回答我的问题如下：局部最小值值得我们关注，因为，首先，它们帮助我们更深入地思考当我们通过梯度下降训练网络时真正发生的事情，其次，因为局部最小值是——或者至少是 — 被认为是在现实生活系统中成功实施神经网络的重大障碍。

在第 5 部分中，我们考虑了如下所示的“错误碗”，我将训练描述为对这个碗中最低点的追求。

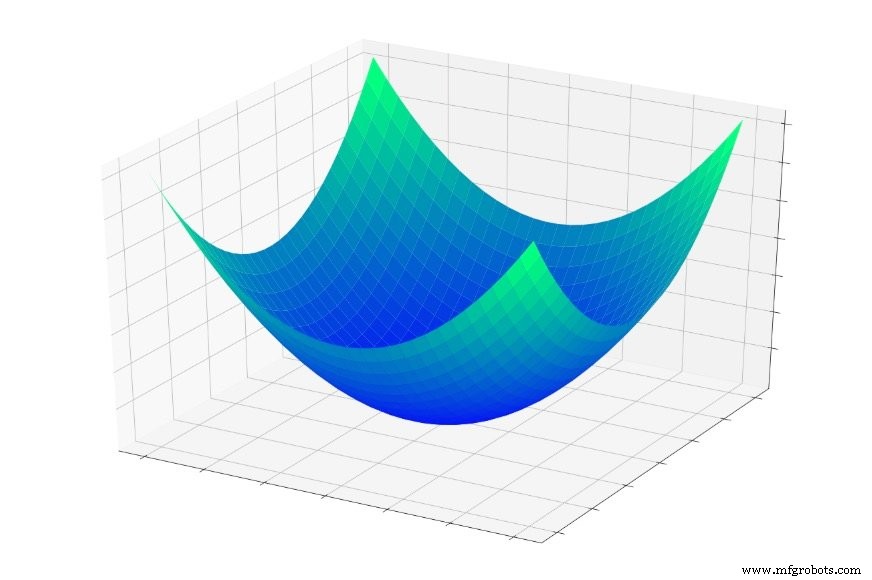
（注意：在整篇文章中，我的图像和解释将依赖于我们对三维结构的直观理解，但请记住，一般概念不限于三维关系。事实上，我们经常使用维数远远超过两个输入变量和一个输出变量的神经网络。）

如果你跳进这个碗里，你每次都会滑到底部。 无论您从哪里开始 ，您将在整个误差函数的最低点结束。这个最低点是全球最低点 .当网络收敛到全局最小值时，它优化了对训练数据进行分类的能力，并且理论上 ，这是训练的基本目标：继续修改权重，直到达到全局最小值。

然而，我们知道，神经网络能够逼近极其复杂的输入-输出关系。上面的错误碗并不完全适合“极其复杂”的类别。它只是函数 \(f(x,y) =x^2 + y^2\) 的图。

但是现在想象一下错误函数看起来像这样：

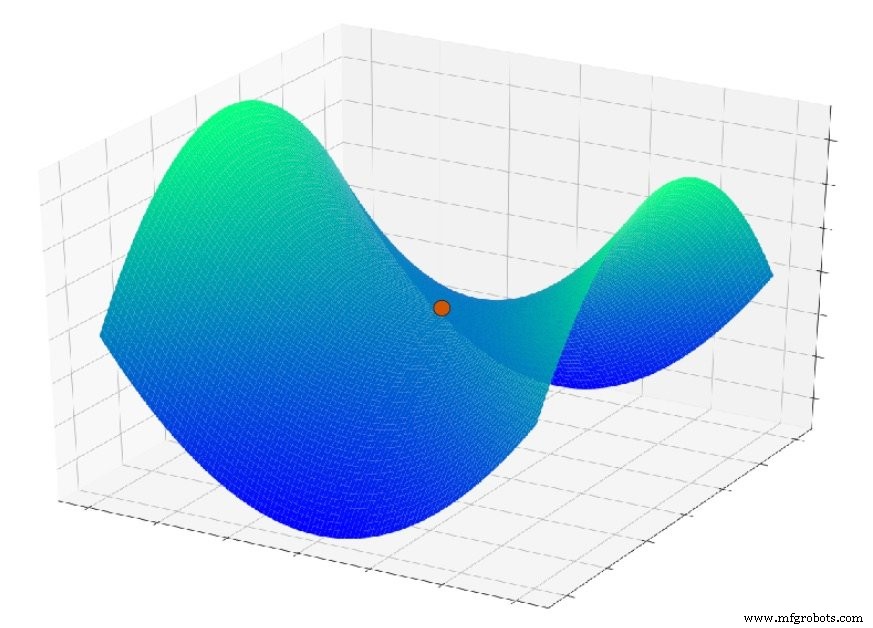
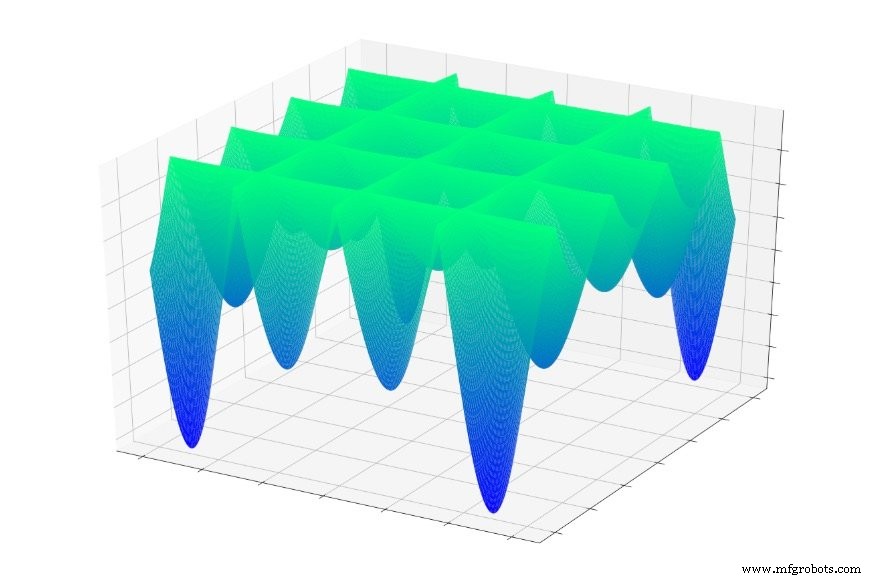
或者这个：

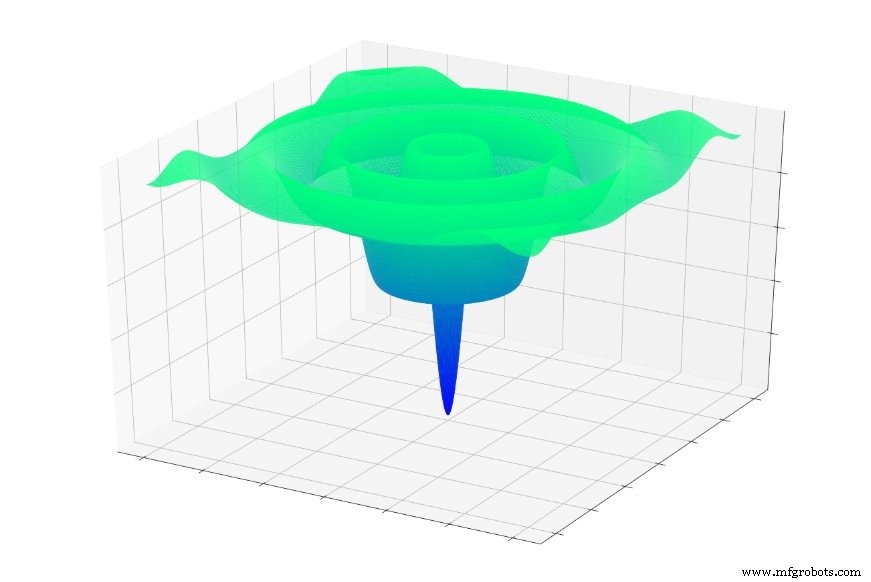
如果您随机跳入这些函数之一，您通常会滑入局部最小值。您将处于图表局部部分的最低点，但您可能离全局很远最低限度。

同样的事情也可能发生在神经网络上。梯度下降依赖于local 我们希望这些信息能够引导网络走向全球最低限度。网络对整体误差面的特征没有先验知识，因此当它到达一个点时，它似乎是基于局部信息的误差面的底部，它无法拉出地形图并确定它需要上坡为了找到实际上比所有其他点都低的点。

当我们实现基本的梯度下降时，我们是在告诉网络，“找到错误表面的底部并留在那里。”我们并不是说，“找到错误表面的底部，记下您的坐标，然后继续上坡和下坡，直到找到下一个。完成后告诉我。”

可以合理地假设全局最小值代表最优解，并得出局部最小值存在问题的结论，因为训练可能“停滞”在局部最小值而不是继续向全局最小值前进。

我认为这个假设在很多情况下都是有效的，但最近对神经网络损失面的研究表明，高复杂度网络实际上可能受益于局部最小值，因为找到全局最小值的网络将被过度训练，因此会更少处理新输入样本时有效。

另一个在这里起作用的问题是称为鞍点的表面特征；您可以在下图中看到一个示例。可能在实际神经网络应用的背景下，误差曲面中的鞍点实际上比局部最小值更重要。

我希望你喜欢这个关于局部最小值的讨论。在下一篇文章中，我们将讨论一些帮助神经网络达到全局最小值的技术（如果这确实是我们想要的）。

工业机器人