使用平面纳米孔板在连续介质中由双束缚态引起的高质量因子双波段 Fano 共振

介绍

可以通过使用高质量 (Q) 因子响应来实现增强光与物质之间的相互作用，这对于提高光学器件的性能具有重要意义 [1]。 Fano 共振的特点是不对称的线形和尖锐的光谱轮廓，为实现光学超材料中的高 Q 因子提供了一种有效的方法，并受到了极大的关注 [2]。在过去的十年中，在许多由等离子体纳米结构启用的纳米级振荡器系统中报道了 Fano 共振 [3, 4]，其中 Fano 共振是由金属-电介质界面处的表面等离子体共振激发的。尽管金属超材料是光操纵的有希望的候选者，但由于金属固有的欧姆损耗，等离子体超材料中的 Fano 共振通常在可见光到近红外 (NIR) 光谱区域受到低 Q 因子的影响。

另一方面，全介电超材料提供强 Mie 型共振，其感应位移电流类似于等离子超材料，但在可见光至 NIR 范围内具有较小的耗散损耗 [5]。由于电和/或磁偶极共振的激发，入射光的能量可以高度集中在介电纳米结构中，这减少了耗散损耗并实现了电场和磁场的大幅共振增强。近年来，连续介质中的束缚态 (BIC) 已成为在全介电超材料中实现高 Q 因子响应的最有希望的方案 [6, 7]。 BIC 位于扩展状态的连续谱内，但违反直觉地保持在空间中的完美定位，理论上具有无限的寿命 [8, 9]。尽管由于非辐射特性，无法从连续光谱中观察到 BIC，但当 BIC 转化为准 BIC (QBIC) [10, 11] 时，可以实现高 Q 因子 Fano 共振，潜在的应用包括定向激光[12]、光学滤波器[13]、非线性频率转换[14]、超灵敏传感器[15、16]和光学涡旋光束[17]。

通常，由于其干涉性质，BIC 的形成与光子结构的对称性（平面和垂直对称性）密切相关。更具体地说，BICs 可以通过斜入射或对称性破坏的纳米结构受到扰动，并且 QBICs 可以实现为本征态和自由空间之间的辐射通道打开 [18, 19]。然而，大多数用于激发具有高 Q 因子的 QBIC 的介电纳米结构是复杂的，例如不对称纳米交叉 [20]、不对称纳米环 [21]、不对称纳米棒 [22,23,24] 和不对称纳米棒 [25,26， 27,28]，由于需要将深亚波长狭缝 [20,21,22,23,24] 或纳米孔 [25,26,27,28] 插入光子结构，这在制造中具有挑战性。其他纳米结构，如重塑的矩形条 [29, 30] 具有增加的锋利边缘，使它们更难以通过传统的光刻技术精确制造，由于开口额外的泄漏通道 [31, 32]。此外，倾斜的纳米棒 [33, 34] 是另一种类型的结构，难以精确控制纳米棒的方向，并且在纳米制造过程中保持谐振器之间的深亚波长空间。在应用中，使用具有更简单结构的全介电超材料（如纳米结构平板）来实现 BIC 和高 Q 因子 Fano 共振是有意义的 [35,36,37,38]。此外，多个 Fano 共振在增强多频带谐波生成 [39]、多通道传感 [40] 和光发射 [41] 等应用中非常有用。因此，使用基于 QBIC 激发的相对简单的架构来实现高 Q 因子多重 Fano 共振具有显着的优势。

在这项工作中，提出了一种由四聚孔组成的新型平面纳米孔板 (PNS)，以实现高 Q 因子双波段 Fano 共振。通过沿超晶格的对角线缩小或扩大 PNS 的四聚孔，两个 QBIC 被激发，两个 Fano 共振的位置及其 Q 因子可以灵活调整。执行超晶格的远场多次分解和近场分布以揭示PNS的谐振特征，表明双频带Fano谐振是由电环形偶极子或磁环形偶极子之间的谐振耦合引起的。 PNS的双频Fano共振具有偏振无关的特性，即使PNS的几何参数发生显着改变，它们也能幸存下来，使其更适合潜在应用。

方法

晶格结构与设计

图 1 显示了所提出的 PNS 的几何示意图及其透射光谱。 PNS由四个纳米孔组成，它们可以沿着超晶格对角线的位移距离Δ> 0收缩（Δ <0）或扩展（Δ> 0），而Δ =0对应于周期减半的简单晶格，其中每个纳米孔都位于超晶格四分之一区域的中心。 PNS的周期和高度分别为Λ和H；纳米孔的半径是 r . PNS的折射率为n s =3.2，背景为空气，折射率为n 一 =1. 图 1c 显示了 PNS 的光谱作为 Δ 位移距离的函数，其中 PNS 被垂直入射 x 照亮 -偏振光。本文介绍的 PNS 的光谱和电磁场分布是通过使用 COMSOL Multiphysics 的有限元法商业软件计算得出的。如图 1c 所示，Δ =0 的非收缩 PNS 没有 Fano 共振。但是，可以通过以下方式获得两个具有 100% 调制深度（定义为 Fano 峰和 Fano 倾角之间的传输差异）的 Fano 共振稍微缩小或扩大纳米孔。与未收缩PNS的传输响应相比，收缩PNS的传输响应变化剧烈，而边带几乎保持不变。

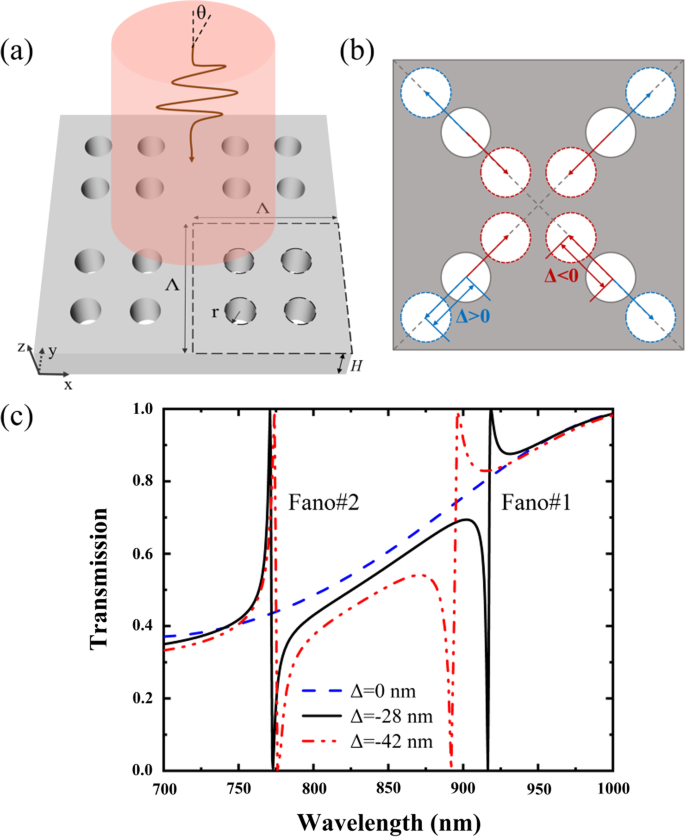
一 PNS 的透视图。 b 当四个纳米孔沿超晶格的对角线收缩（Δ <0）或扩展（Δ> 0）时，PNS的垂直视图。 c PNS 的透射光谱作为 Δ 位移距离的函数。 PNS 在 x 的照明下 -入射角为θ的偏振入射波 =0. PNS 的参数为：Λ =350 nm, r =35 纳米和 H =175 纳米

为了清楚地显示由四聚化孔的收缩或扩展引起的双频带 Fano 共振的演变，作为 Δ 位移距离的函数的 PNS 的透射二维图如图 2a 所示。如图 2a 所示，当 Δ =0 时，在感兴趣的波长区域中出现了两个 BIC，并且先前在双光栅超膜 [13] 和裂环谐振器 [21] 的结构中报道了类似的双 BIC 现象。在 Δ ≠ 0 的情况下，由于 PNS 的对称性破坏，即从简单晶格的中心对称性到超晶格的四重旋转 (C4) 对称性，BICs 被诱导为 QBICs，从而实现了双波段 Fano 共振。此外，由于四聚孔沿超晶格的对角线收缩或扩展时可以保持 PNS 的 C4 对称性，因此对于相同的绝对值 |Δ|，PNS 的透射光谱是相同的。原则上，当 PNS 的晶胞从简单晶格变为超晶格时，四聚孔的收缩或膨胀会减小 PNS 的第一个布里渊区的面积，并且对称保护的 BIC 可以在垂直入射时被激发。引入表面扰动以及 PNS 的布里渊区折叠 [42, 43]。通常，对称保护 BIC 的 Q 因子显示出对不对称程度 δ 的平方反比依赖性 基于微扰理论[21]：

$$Q_{fit} =\kappa \cdot \frac{cS}{{\omega \cdot \delta^{2} }},$$ (1)

其中 ĸ 是比例常数，S 是超晶格的面积，ω 是角频率，不对称参数是 \(\delta { =}\sqrt 2 \Delta /\Lambda\).

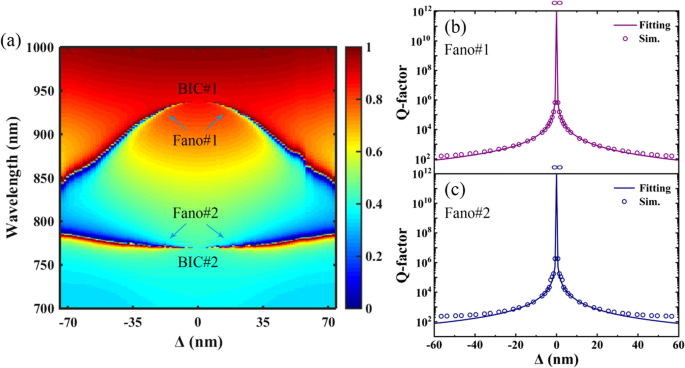
一 作为沿超晶格对角线的 Δ 位移距离的函数的 PNS 的透射二维图。 b 和 c 分别为 Fano#1 和 Fano#2 的 Q-factor 和拟合结果。其他参数同图1c

图 2b、c 分别显示了 Fano#1 和 Fano#2 的 Q 因子和拟合结果。 PNS 的 Q 因子计算为谐振波长 λ 之间的比率 r 及其半峰全宽 (FWHM) Δλ，其中 Δλ 是法诺共振峰和谷之间的波长区域。 PNS 的拟合结果通过使用等式计算。 (1).如图 2b、c 所示，通过使用平方反比关系拟合数据，验证了 PNS 的发散轨迹，其中 Q 因子在 Δ =0 处发散到无穷大。可以获得很好的拟合结果，较大的不对称性的轻微分歧是由于偏离方程中微小扰动的假设。 (1). PNS 的显着优点是可以通过缩小或扩大四聚孔来定制双频 Fano 共振的位置和 Q 因子，这有利于对高 Q 因子倍数的谐振性能进行动态控制。范诺共振。

物理机制和解释

为了通过缩小或扩大 PNS 的四聚化孔洞来深入了解双波段 Fano 共振的起源，我们将 BIC 和 Fano 共振的远场辐射分解为不同多极组件的贡献，以进一步讨论它们的特征。多极矩可以根据位移电流密度j计算 在 PNS [26, 44, 45] 的超晶格中：

$${\varvec{P}} =\frac{1}{i\omega }\int {{\varvec{j}}d^{3} r} ,$$ (2) $${\varvec{M }} =\frac{1}{2c}\int {\left( {{\varvec{r}} \times {\varvec{j}}} \right)d^{3} r} ,$$ (3 ) $${\varvec{T}} =\frac{1}{10c}\int {\left[ {\left( {{\varvec{r}} \cdot {\varvec{j}}} \right) {\varvec{r}} - 2r^{2} {\varvec{j}}} \right]} d^{3} r,$$ (4) $${\varvec{Q}}_{\alpha ,\beta }^{\left( e \right)} =\frac{1}{i2\omega }\int {\left[ {r_{\alpha } j_{\beta } + r_{\beta } j_{ \alpha } - \frac{2}{3}\left( {{\varvec{r}} \cdot {\varvec{j}}} \right)}\delta _{\alpha ,\beta }\right] } d^{3} r$$ (5) $${\varvec{Q}}_{\alpha ,\beta }^{\left( m \right)} =\frac{1}{3c}\int {\left[ {\left( {{\varvec{r}} \times {\varvec{j}}} \right)_{\alpha } r_{\beta } + \left( {{\varvec{r} } \times {\varvec{j}}} \right)_{\beta } r_{\alpha } } \right]d^{3} r} ,$$ (6)

其中 P , M , T , 问 ^{(e )} 和问 ^{(米 )} 分别为电偶极子（ED）、磁偶极子（MD）、环形偶极子（TD）、电四极子（EQ）和磁四极子（MQ）的矩； c 是真空中的光速，α , β =x , y , z .这里的电荷密度ρ ，通常出现在 ED 和 MQ 的定义中，已被置换电流密度 j 通过 \(i\omega \rho + \nabla \cdot {\varvec{j}} =0\) 的电荷守恒关系。在谐波激励 ~ exp(iωt )，对远场响应有贡献的感应多极矩的散射功率可写为：

$$\begin{aligned} I &=\frac{{2\omega^{4} }}{{3c^{3} }}\left| {\varvec{P}} \right|^{2} + \frac{{2\omega^{4} }}{{3c^{3} }}\left| {\varvec{M}} \right|^{2} + \frac{{2\omega^{6} }}{{3c^{5} }}\left| {\varvec{T}} \right|^{2} + \frac{{\omega^{6} }}{{5c^{5} }}\sum\limits_{\alpha ,\beta } {\left | {{\varvec{Q}}_{\alpha ,\beta }^{\left( e \right)} } \right|}^{2} \\ &\quad+ \frac{{\omega^{6} }}{{20c^{5} }}\sum\limits_{\alpha ,\beta } {\left| {{\varvec{Q}}_{\alpha ,\beta }^{\left( m \right)} } \right|}^{2} + {\text{o}}(\omega), \end {对齐}$$ (7)

其中前两项对应于传统的 ED（电荷）和 MD 散射。第三项对应于TD散射。第四和第五项来自EQ和MQ。最后一项是高阶项，包含它们之间的高阶多极散射和耦合，一般可以忽略。通过使用方程。 (2)-(7)，可以得到不同多极子对远场散射能力的贡献。

图 3 显示了不同 Δ 位移距离下 PNS 不同多极子的散射能力，其他参数与图 1c 相同。如图 3a-d 所示，对于 Δ =0 的 PNS，ED 和 MD 是主要偶极子，它们在感兴趣的波长区域不谐振。然而，通过以 |Δ|≠ 0 缩小或扩大 PNS 的纳米孔，由于共振偶极子模式的激发，可以实现双频带 Fano 共振。为了清楚地看到共振偶极子模式在形成观察到的双波段 Fano 共振中的重要作用，图 3e，f 显示了不同多极子的归一化散射能力，其中 Δ =− 28 nm，分别围绕 Fano#1 和 Fano#2 .如图 3e 所示，主要谐振模式是 Fano#1 周围的 ED 和 TD，而 Fano#1 是电环形偶极子谐振耦合的直接结果。特别是，ED 和 TD 在 Fano#1 的谐振尖端 (918.5 nm) 处强烈增强到相当的幅度；因此，由于 ED 和 TD 之间的破坏性干扰，可以获得 100% 的传输。而对于 Fano#1 的共振倾角 (916.5 nm)，由于 ED 和 TD 的散射增强，反射最大化并且透射率变为零。类似地，如图 3f 所示，Fano#2 是由磁环形偶极子的共振耦合产生的，其尖端 (771.1 nm) 表示 MD 和 TD 之间的相消干涉，而其倾角 (772.9 nm) 与MD 和 TD 的增强散射。请注意，由于电环形偶极子或磁环形偶极子的强耦合，即使 Δ 变化，Fano#1 和 Fano#2 的谐振模式也是稳健的。

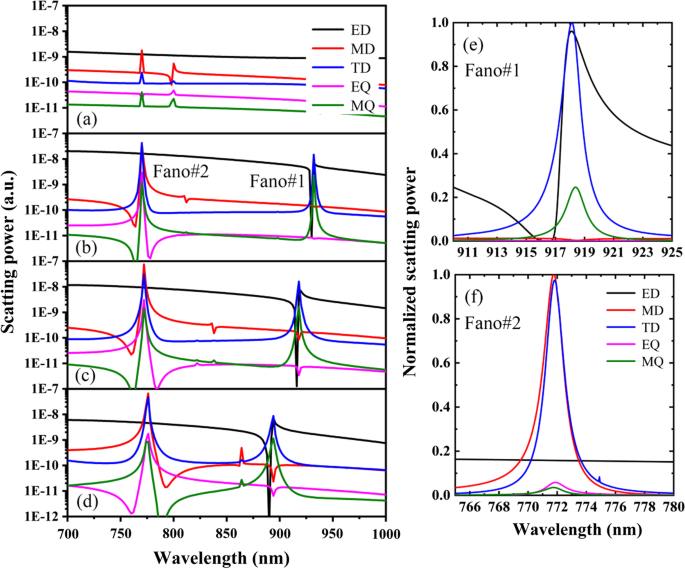
a 时笛卡尔 ED、MD、TD、EQ 和 MQ 的散射能力 Δ =0, b Δ =− 14 nm，c Δ =− 28 nm 和 d Δ =- 42nm。 e 和 f 分别在 Fano#1 和 Fano#2 周围具有 Δ =− 28 nm 的不同多极杆的归一化散射能力。其他参数同图1c

为了将远场中双频 Fano 共振的传输响应与感应多极矩的激发联系起来，PNS 超晶格的 Fano 共振的电磁场和位移电流分布如图 4 所示。图 4a、b，Fano#1 的电场被很好地限制在 PNS 的超晶格中，位移电流沿 x 轴，表示 ED 谐振模式。而且，Fano#1 的位移电流在超晶格的中心和边缘之间形成两个反向回路，磁场在yz形成一个回路 平面，对应于沿 x 的 TD 共振模式 轴 [44, 46]。因此，Fano#1 是由 ED 和 TD 模式之间的共振耦合产生的，这与上述多极分解的预测结果一致。事实上，由于 Fano#1 环形电偶极子的谐振特性，Fano 的谐振峰值 (918.5 nm)、中心波长 (917.5 nm) 和谐振倾角 (916.5 nm) 处的电磁场和位移电流分布#1 几乎相同，只是场振幅略有不同（附加文件 1：图 S1）。在 Fano#2 的情况下，如图 4c 所示，电场强烈增强，位移电流在超晶格中心和 PNS 的相邻超晶格之间形成两个反向回路，表明沿 TD 谐振模式z 轴。此外，Fano#2 的磁场高度局域化在超晶格中，方向沿 y 轴，如图 4d 所示，具有 MD 共振模式。因此，Fano#2 是磁环偶极子谐振耦合的直接结果，这与 PNS 远场多极分解的预测一致。此外，由于 Fano#2 的磁环形偶极子的耦合，Fano#2 共振峰 (771.1 nm)、中心波长 (772.0 nm) 和共振倾角 (722.9 nm) 处的电磁场和位移电流显示相似分布（附加文件 1：图 S2）。

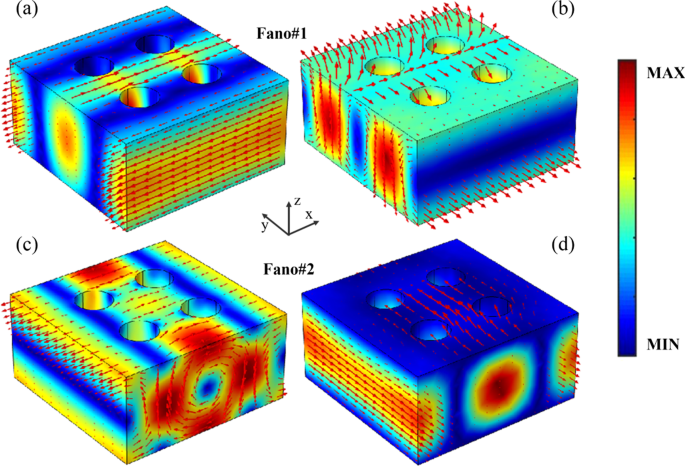
PNS超晶格Fano共振的电磁场和位移电流分布，颜色条代表场幅值，红色箭头表示场矢量或位移电流矢量。其他参数与图 1c 相同，Δ =− 28 nm。 一 和 c Fano#1 和 Fano#2 的电场幅值和位移电流矢量分布。 b 和 d Fano#1和Fano#2的磁场幅值和磁场矢量分布分别

结果与讨论

图 5 显示了作为半径 r 函数的 PNS 的透射光谱 纳米孔，其他参数与图 1c 相同，Δ =− 28 nm。如图 5a 所示，双频 Fano 共振可以保持为 r 从 0 到最大值 67.5 nm，即 ，四聚化的孔在超晶格中彼此相切。纳米孔半径的增加 r 增加 PNS 的表面扰动并降低其有效折射率 (ERI)，导致 Q 因子增加和 Fano 共振蓝移。具体来说，Fano#1 的共振位置对 r 的变化更敏感 ，并且随着四聚化孔彼此接近，双频带 Fano 共振倾向于合并为一种共振模式。如图 5b 所示，r 的增加 不仅使 Fano 共振的共振位置发生蓝移，而且还增加了它们的 FWHM。作为 r 从 25 nm 增加到 45 nm，Fano#1 和 Fano#2 的共振峰分别从 936.7 nm 和 793.2 nm 蓝移到 887.6 nm 和 743.8 nm；并且它们的 FWHM 分别从 0.8 nm 和 0.6 nm 增加到 6.8 nm 和 3.1 nm。注意r的增加 还提高了 Fano 共振的调制深度，100% 调制深度可以实现为 r 大于 30 纳米。此外，通过评估 PNS 结构参数对 Fano 峰值波长的偏移，表明纳米孔半径 r 是 Fano#1 和 Fano#2 最敏感的结构参数（附加文件 1：图 S3）。因此，r 的变化 为动态控制PNS双频Fano谐振的谐振性能提供了一种有效的方法。

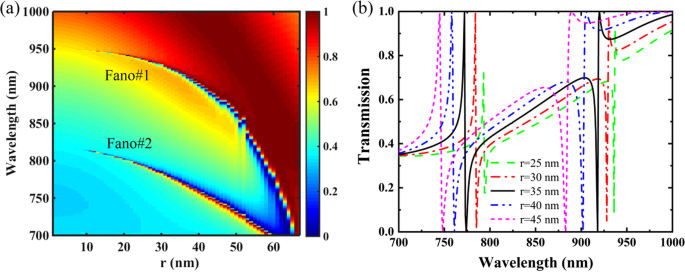
一 作为半径函数的 PNS 传输二维图 r 的纳米孔。 b 不同纳米孔半径的PNS透射光谱r .其他参数与图 1c 相同，Δ =− 28 nm

图 6 显示了结构的对称性对 PNS 传输响应的影响，其中半径 r' 两个纳米孔的距离从零变化到彼此相切，其他参数与图 1c 相同，Δ =− 28 nm。如图 6a 所示，对于沿 x 镜像对称的超晶格 轴（入射光的电场方向），为半径 r 两个纳米孔的 ' 增加，双波段 Fano 共振的共振位置由于 PNS 的 ERI 降低而蓝移，并且由于增加的表面扰动，它们的带宽变宽。然而，如图 6b 所示，虽然随着 r 的增加可以保持两个 Fano 共振 '，两个额外的 Fano 共振将发生作为超晶格沿 x 的镜像对称 轴断了。一般来说，打破沿 x 的结构对称性 (y ) 轴也会破坏模式沿 x 的对称性 (y ) 周期晶格的轴，并且非辐射非简并模式由于其简并分量而能够耦合到外部辐射 [47]。因此，事实上只有沿 x 的镜像对称破坏结构存在两个额外的 Fano 共振 轴表示它们是由于扰动的非退化模式造成的。

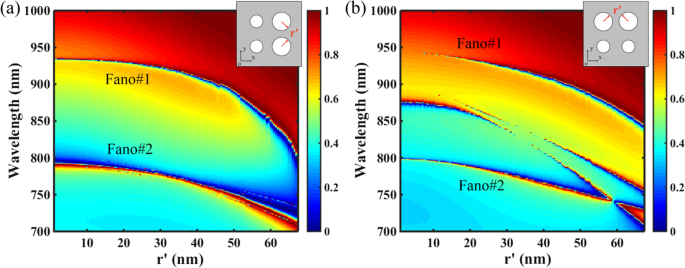
结构对称性对 PNS 传输响应的影响。其他参数与图 1c 相同，Δ =− 28 nm。插入图显示了 PNS 超晶格的示意图。 一 作为半径函数的 PNS 传输二维图 r ' 两个纳米孔，其中超晶格沿 x 的结构对称性 轴保持不变。 b 作为半径函数的 PNS 传输二维图 r ' 两个纳米孔，其中超晶格沿 x 的结构对称性 轴断了

我们进一步表征了 PNS 在入射角和偏振角影响下的谐振性能。如图 7a 所示，由于 C4 对称拓扑结构，PNS 的双频 Fano 共振不受极化角变化的影响。随着偏振角从 0° 变为 90°，即从 x -极化到 y -polarization，Fano#1 和 Fano#2 保持不变。然而，在入射角的情况下，如图 7b 所示，虽然 Fano#1 也对入射角的变化不敏感，但 Fano#2 随着入射角偏离法向入射而发生红移，并且额外的 Fano 共振(Fano#3) 的发生是由于对称保护 BIC 的辐射衰减抑制在非正常入射时被取消。通常，BIC 的这种类型的辐射衰减抑制与周期晶格阻带的两个边缘之一处的两个反向传播的泄漏模式发射的辐射场之间的相消干涉密切相关 [48]。注意由于 Fano#2 和 Fano#3 之间的强耦合，可以在它们之间的附近区域激发一个狭窄的诱导透明窗口。

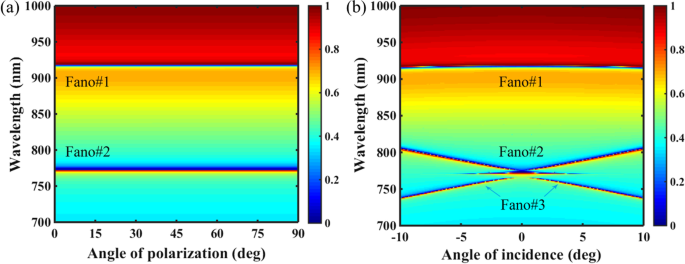
一 作为偏振角函数的 PNS 的透射二维图。 b 作为入射角函数的 PNS 的透射二维图。其他参数与图 1c 相同，Δ =− 28 nm

最后，我们表明可以通过增加 PNS 的平板高度 H 来获得多个 Fano 共振。图 8 显示了非收缩 (Δ =0 nm) 和收缩 (Δ =− 28 nm) 结构的 PNS 透射二维图，作为 H 的函数。如图 8a 所示，随着 H 的变化，除了非收缩 PNS 的 Fabry-Pérot (F-P) 共振之外，没有 Fano 共振。根据F-P理论，非收缩PNS的F-P腔共振条件可写为：

$$\delta =(2\pi /\lambda ) \cdot H \cdot n_{eff} + \varphi =m\pi ,$$ (8)

其中 δ 是相移，λ 是自由空间中的波长，n 效果 是 PNS 等效均质板的 ERI，φ 是附加相位和 m 是表示共振次数的整数。利用有效介质理论[49]，PNS的ERI可以估计为：

$$n_{eff} =\sqrt {\frac{{\left[ {\left( {1 - f} \right)n_{a}^{2} + fn_{s}^{2} } \right] \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right] + n_{s}^{2} }}{{2 \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right]}}} ,$$ (9)

其中 f 是 PNS 的填充因子，f =1 − 4π(r /Λ) ² .

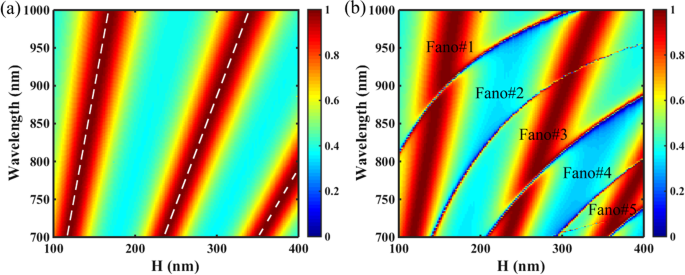
一 PNS 的透射二维图作为板高度 H 的函数，Δ =0 nm，白色虚线是 F-P 腔模型的结果。 b 作为平板高度 H 函数的 PNS 透射二维图，Δ =− 28 nm。其他参数同图1c

通过使用方程。 (8)和(9)，非收缩PNS的F-P共振位置可以计算为λ F–P =2π ·H·n 效果 /(mπ -φ ）。在计算中，虽然附加相位φ 不能视为常数，因为它明显影响相移 δ ，它的值可以通过使用线性拟合方法来计算[50, 51]。图 8a 显示了 PNS 的透射二维图，Δ =0 nm，F-P 理论的结果由白色虚线表示。如图 8a 所示，F-P 腔模型的白色虚线与 PNS 的传输峰重合，证实是 F-P 共振增强了非收缩 PNS 的传输感兴趣的光谱区域。然而，如图 8b 所示，对于 Δ =− 24 nm 的收缩 PNS，当 H 在 100-400 nm 范围内变化时，五个具有高 Q 因子的 Fano 共振被激发并与 F-P 共振共存，Fano 共振非常强烈，以至于它们在 Fano 和 F-P 共振之间的交叉区域分裂了 F-P 共振。根据平板波导理论，光子晶体平板厚度的增加确保了更多的泄漏模式限制在结构中[32, 52]；因此，仅通过增加 PNS 的厚度就可以增加 Fano 共振的数量。注意四聚孔的移动不会改变PNS的ERI，因此对于非收缩结构和收缩结构，F-P共振的位置几乎保持相同。

结论

通过使用基于双 QBIC 激励的相对简单的 PNS 架构，可以实现高 Q 因子双频 Fano 谐振。通过沿超晶格的对角线缩小或扩大 PNS 的四个纳米孔，两个对称保护的 BIC 可以转换为双频 Fano 共振，并且它们的位置和 Q 因子可以灵活调整。 PNS的双频Fano共振是由电环偶极子或磁环偶极子之间的共振耦合引起的，验证了它们的远场多次分解与超晶格近场分布之间的相关性。 PNS 的双频 Fano 共振具有偏振无关特征，其高 Q 因子特征对几何参数的变化具有鲁棒性。通过增加 PNS 的高度，可以提高高 Q 因子 Fano 共振的数量，因为该结构可以支持更多的泄漏模式。我们的研究结果为实现具有更好性能的高 Q 因数谐振器提供了更多的调谐自由，这可能为激光、传感和非线性光子学的发展提供进一步的支持。

数据和材料的可用性

当前研究中使用和/或分析的数据集可根据合理要求向相应作者索取。

缩写

Q 因子：

品质因数

PNS：

平面纳米孔板

BIC：

连续体中的束缚态

近红外：

近红外

QBIC：

准BIC

FWHM：

半高全宽

编辑：

电偶极子

MD：

磁偶极子

TD：

环形偶极子

情商：

电动四极杆

MQ：

磁性四极杆

ERI：

有效折射率

F–P：

法布里-佩罗