通过优化反射面涂层实现分布式反馈量子级联激光器的稳定单模操作

背景

中红外量子级联激光器 (QCL) [1] 是许多商业应用中最有前途的光源之一。这些实际应用，如气体传感、自由空间通信和高分辨率光谱 [2,3,4,5] 将需要具有高功率、提高单模可靠性和低成本的 QCL。因此，自 1997 年首次展示分布式反馈 (DFB)-QCL 以来 [6]，随着室温连续波 (CW) 操作的演示，这些设备的性能得到了极大的提升中红外区域 [7,8,9,10]。然而，大多数基于埋入式光栅结构的 DFB-QCL 都会存在决定激光频率模式的随机劈裂面的问题。由于两种带边模式的损耗量相同，无法保证稳定的单模操作 [11]。尤其是在高温条件或大注入电流下，总会发生跳模现象，不利于这些单模器件的应用。

为了获得稳定的单模工作，在光栅周期引入四分之一波相移（λ/4 PS），使激光器工作在缺陷模式；因此，可以避免两种带边模式之间的竞争。但是必须使用电子束光刻来制造 λ/4 PS 光栅，这既耗时又昂贵 [12]。增益耦合 DFB 激光器是实现传统半导体激光器稳定单模操作的不错选择 [13]。然而，QCL制作增益耦合DFB激光器是不现实的，因为蚀刻有源区会造成很大的损失。另一种巧妙的方法是使用腔损耗耦合机制来增加两个 DFB 模式之间的差异损耗。相信适当的反射率刻面涂层即使在高温和大电流下也能实现稳定的单模操作。虽然有一些研究致力于刻面涂层，但他们始终专注于形成最佳等效腔长度L 选择保持激光器的壁插效率 (WPE) 而不是单模可靠性 [14, 15]。此外，优化的反射率涂层应该是解决两种DFB模式之间竞争的一种很有前景的方法，值得系统地研究。

在本文中，DFB-QCLs 在 λ 的稳定单模运行 ~ 4.76 μm 在抗反射 (AR)/高反射 (HR) 涂层后呈现。 AR 涂层由 Al2O3 (380 nm) 和 Ge (33 nm) 的双层电介质组成。这些器件的阈值电流密度非常低，为 0.65 kA/cm ² 在 20°C。单模发射的边模抑制比 (SMSR) 高于 26 dB，在 CW 操作中可在高达 90 °C 的温度下实现，没有任何模式跳变。认为正面的抗反射涂层对于抑制腔面的随机相位非常有价值。

方法

理论与仿真

有限DFB腔减反射涂层效应仿真的核心是计算两种带边模式的模式损耗。传递矩阵法将是分析整个激光器结构的合适方法 [16, 17]。我们考虑将这种方法应用于具有类似于图 1 所示纵向折射率分布的器件。该示意图说明了具有小的不同有效折射率扰动 (n) 的光栅的效果 eff,1, n eff,2) 和涂层薄膜 (n 3、n 4）关于引导模式。计算中使用的主要材料的复折射率如下：InP(3.088 + i*2e-4)、InGaAs(3.4 + i*2.9e-5)、有源区(3.298 + i*4e-5)、高掺杂 InP (2.81 + i*1.4e-2)、SiO2 (1.3603 + i*6.3e-4)、Au (1.341 + i*32.582)、Al2O3 (1.5348 +296i)、Ge)*7 (4.0165 + i*4e−2)。那么，不同的有效索引n eff,1 =3.1599 + i*5.17e−5 和 n eff,2 =3.1662 + i*5.6756e−5 由 COMSOL 通过偏微分方程 (PDE) 函数计算得出。假设激光器以单横模工作，因此光在沿激光腔的每一点的传播特性由单个标量复数 k 描述 ，它是介质的波矢。进一步认为激光是线偏振的，其相关电场具有正弦时间依赖性e ^{i ωt} . 根据上面给出的这些假设，一维平面电磁波因子 E z，描述波函数的特殊变分部分，满足亥姆霍兹方程

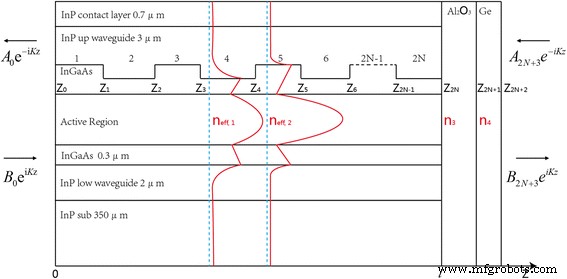
纵向光模分布上带有减反射涂层的有限DFB腔模型示意图

K (z) 由

其中 ω 和 c 分别是角频率和光速和n (z) 是沿激光腔每个点的复折射率。波矢k 需要解决的问题可以分为两部分：k r 和 k 一世。实部 k r 决定了激光腔中光的波长，而虚部 k i 源自有限腔的模式损耗，用于衰减。从图 1 可以看出，激光器可以被认为是一个多节装置，具有 2N + 2 个部分，其中 N 是光栅周期。在每个部分中，电场 E n(z) 是两个反向传播的指数平面波的线性组合，其中一个以复振幅 A 递减 n 和另一个随着 B 增加 n.方程描述如下：

总共有 2N + 3个接口。在这些界面的每一个上，电场及其相对于传播方向的导数在界面两侧必须相等。得到方程如下：

传递矩阵M (d n ) 由

考虑到电泵浦激光器是一种自激振荡装置，没有来自装置外部的入射波。这导致边界条件 B 0 =A 2N + 3 =0，方程变为

波矢k的每个值 可以在 Matlab 的帮助下通过方程获得。 (6).虚部 k i 对应的腔模损耗有助于分析增透膜效应。

图 2a 展示了基于传递矩阵模拟的计算结果。如两条红色曲线所示，高频模式损耗随着反射率的降低而变化非常缓慢，而低频模式则急剧增加。插图显示了在光栅的单个周期内为低频和高频模式计算的模式分布。如图所示，低频模式在光栅的高折射率部分的光栅峰值中具有更高的电场强度，并且高频模式更集中在光栅的低折射率部分。对于没有小平面反射率的无限腔模型，高频模式总是比低频模式具有更低的模式损耗。如果可以忽略端面镜的影响，那么波导损耗较小的高频模式将始终产生激光。然而，端面反射镜的存在会产生相长或相消干涉激光腔中 DFB 模式的反射。这种干扰会影响每种模式的有限光栅腔损耗，并可以确定哪种模式产生激光。我们注意到，当两个反射镜的位置与一种 DFB 模式的电场振幅峰值重合时，反射镜的影响最大，这也是当反射镜位于另一种 DFB 模式的节点时。此处，未镀膜面的反射镜与低频模式的峰值重合，然后，来自端面反射镜的反射最大程度地与激光腔中存在的模式相长干涉。由于反射镜的建设性贡献，这导致总模式损耗降低。随着反射率的降低和使用双层增透膜的附加相移影响，由于干涉效应减弱和反射镜损耗增加，低频模式的损失随着反射率的降低而逐渐增加。同时，由于干扰效应增强，高频模式的损失略有变化。这导致 Δ 模式损耗表现得与指数函数类似，尤其是当正面反射率 <0.15 时。根据仿真结果，当前端反射率<0.11时，整个光谱内只存在一个极小点，这意味着理论上不会发生模式跳变，因为另一个带边模式损耗太高而无法发射。

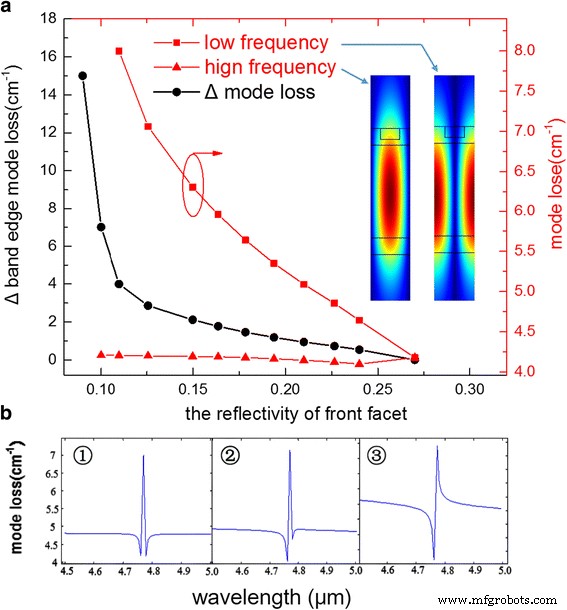
一 两条红色曲线分别是高频和低频模式的模式损耗。黑色曲线是标记为 Δ 的两个带边模式之间的差模损耗。插图显示了在光栅的单个周期内为低频和高频模式计算的模式分布。 b 不同增透膜传输矩阵模拟计算的模态损耗谱

图 2b 显示了模拟过程中的三个典型模式损耗谱，其中高频和低频模式分别为 4.762 和 4.779 μm。第一个是没有增透膜的 DFB-QCL。我们可以清楚地看到源于光栅反馈的阻带，并且两种带边模式几乎相同。第二种是具有 200 nm Al2O3 和 5 nm Ge 的特定增透膜，反射率为 0.22。两种带边模式之间的差异开始变得明显。最后一个表明，在较低的反射率涂层下，Δ模式损失如此之大，以至于低频模式淹没在阻带损失之下。虽然理论上反射率越低，Δ模式损耗就越大，但我们也应该考虑到，极低的反射率会导致器件中巨大的镜面损耗，使WPE急剧下降。这是基于实验选择膜厚的权衡。

设备制造

QCL 晶片生长在 n 掺杂 (Si, 3 × 10 ¹⁷ 厘米 ⁻³ ）基于双声子共振设计的固体源分子束外延（MBE）InP衬底。有源核心包括 40 级应变补偿 In0.669Ga0.331As/In0.362Al0.638As 量子阱和势垒，类似于参考文献。 [18]。层序如下：2-μm下InP包覆层（Si，2.5 × 10 ¹⁶ 厘米 ⁻³ ), 0.3-μm 厚的匹配 In0.47Ga0.53As 层 (Si, 4 × 10 ¹⁶ 厘米 ⁻³ )，40 个有源/注入器级，0.3 微米厚的 In0.47Ga0.53As 层（Si，4 × 10 ¹⁶ 厘米 ⁻³ ), 3-μm 上部 InP 包覆层 (Si, 2.5 × 10 ¹⁶ 厘米 ⁻³ ), 和 0.7-μm 高掺杂 InP 包覆层 (Si, 5 × 10 ¹⁸ 厘米 ⁻³ ）。有源区的平均掺杂水平根据经验调整为2.4 × 10 ¹⁶ 厘米 ⁻³ .为了制造埋入式光栅，将顶部包层向下移至上层 InGaAs 层。周期为Λ =0.755 μm（占空比σ =20%) 使用全息光刻技术在 300 nm 厚的 InGaAs 上层上定义，随后通过湿化学蚀刻蚀刻至约 90 nm 的深度。然后，将 3 μm 厚的低掺杂 (Si, 2.5 × 10 ¹⁶ 厘米 ⁻³ ) InP 层之后是 0.2-μm 逐渐掺杂（从 1 × 10 ¹⁷ 厘米 ⁻³ 到 3 × 10 ¹⁷ 厘米 ⁻³ ) InP 层和 0.5-μm InP (5 × 10 ¹⁸ 厘米 ⁻³ )接触层通过金属有机气相外延(MOVPE)依次完成作为上包层。

在实施光栅图案和再生长之后，外延晶片被蚀刻成 10 微米宽的脊，然后将波导重新引入 MOVPE 系统并埋入半绝缘 InP (Fe) 中。通过等离子体增强化学气相沉积 (PECVD) 沉积 450 纳米厚的 SiO2 层，用于脊周围的绝缘，并通过 Ti/Au 层提供电接触。随后电镀了一个额外的 5 微米厚的金层，以进一步改善散热。波导被切割成 2 毫米长的条，并在具有优化反射面涂层的设备上进行测试。由 Al2O3/Ti/Au/Ti/Al2O3 (400/5/100/10/200 nm) 组成的背面 HR 涂层和由 Al2O3/Ge (380/33 nm) 组成的正面 AR 涂层均通过 e-沉积束蒸发。对于 4.76-μm 波长，计算出的正面反射率为 3.4%，我们之前发表的论文 [19] 中讨论了涂层厚度波动与反射率之间的详细关系。激光器用铟焊料将外延层朝下安装在 SiC 散热器上，然后引线键合到外部接触垫。对于光谱和电学特性，激光器​​安装在珀耳帖元件上，并在散热器上用热敏电阻监测温度。

结果与讨论

图 3 显示了随着电流的增加，亚阈值发射光谱从电致发光动态变化为激光，这是使用 Bruker Vertex 70 FTIR 和氮冷却 HgCdTe 检测器测量的。刚好高于阈值的激光光谱表明器件工作在基模下，当电流为285 mA时，我们可以清楚地得到基模的阻带。从阻带宽度 Δν =3.076 cm ⁻¹ 和有效索引 n eff =1/(2νΛ) =3.153，我们计算一个耦合系数κ =Δν ·π ·n eff =30.4 cm ⁻¹ ，导致我们在耦合产品 κL 中的 HR 涂层 2 毫米长的腔 12.1，这与我们的设备制造非常吻合。 κL的乘积 远大于之前的理论研究κL ≈ 1 [20] 表明获得了过耦合方案，有利于在整个电流和检测温度范围内确保单模。

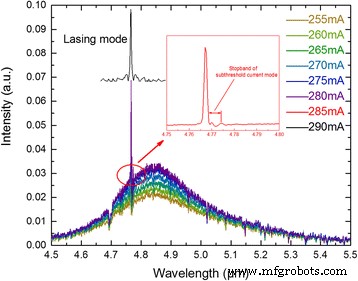
30°C下测量的器件亚阈值直流频谱

图 4a 显示了典型的 CW 功率-电流-电压 (P -我 -V ) 在 20 到 90 °C 之间不同散热器温度下 DFB 激光器的曲线。 2 mm 长器件的输出功率达到 200 mW，阈值电流密度低至 0.65 kA/cm ² 在 20°C。阈值电压 (V 在 20-90 °C 的温度范围内测得的 th) 为 13.2-14.2 V。值得注意的是，模式跳变仅存在于低于 60 °C 的较低散热器温度，这可以从 P 轻松推导出 -我 曲线。较高的散热器温度会对激光器核心产生更严重的热量积累，从而抑制另一种模式激光的热效应和模式跳跃不会发生。图 4b 显示了 P -我 -V DFB 激光器的曲线，在其正面沉积了抗反射 (AR) 涂层，我们选择了 3.4% 的 AR 涂层反射率。每一个平滑的P -我 曲线表明在我们测量的温度周围不存在模式跳变。图 4c、d 显示了 150 到 250 mA 不同电流下的激光光谱，步长为 25 mA。从图 4d 中可以明显看出，我们通过优化的 AR 面涂层而不是图 4c 中的模式跳跃在不同电流周围实现了稳定的单模。频率始终与注入电流保持线性关系，电流调谐系数Δν /ΔI =− 0.024 cm ⁻¹ mA ^-1 证明增透膜是解决DFB-QCL模跳问题的一种简单有效的方法。

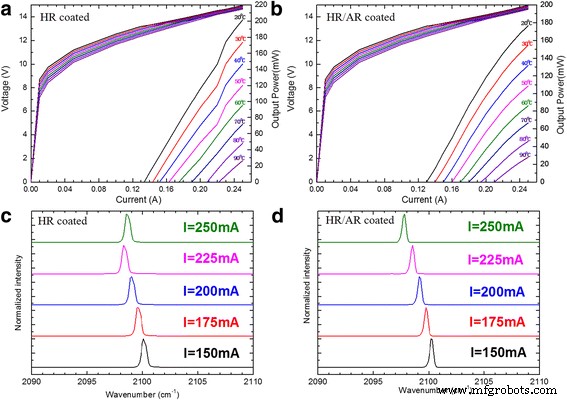
一 , b 在 20 到 90 °C 之间的不同散热器温度以及 V 下，在 CW 模式下运行的 DFB 激光器的输出功率与电流的关系 -我 曲线。 c , d 20 °C、25 mA、150~250 mA不同电流下的连续波激光光谱

图 5 显示了涂层 DFB 激光器在 20 至 90 °C 不同散热器温度下的发射光谱。使用具有 0.25 cm ^-1 的 NICOLET 8700 FTIR 光谱仪进行测量 快速扫描模式下的分辨率。在 90 °C 的高温下，在整个研究温度范围内观察到单纵模发射，边模抑制比 (SMSR) 为 26 dB。如图 5 的插图所示，观察到峰值发射光谱从 2100.4 cm ^-1 在 20 °C 至 2088.6 cm ⁻¹ 在 90 °C 时，对应于温度调谐系数 Δν /ΔT =− 0.168 cm ⁻¹ K ⁻¹ .良好的线性调谐表明在散热器温度变化期间没有发生模式跳跃。此外，由于脊宽的精确控制，所有提到的器件在基模的连续波操作下都显示出主导的单横向远场。

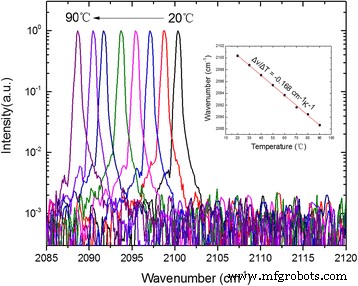
DFB 激光器在 1.1 阈值电流下的单模发射光谱，不同散热器温度为 20–90 °C。插图显示了激光频率随温度的线性拟合调谐特性

CW WPE 被计算并绘制为图 6 中输入电力消耗的函数。在 20 °C 时，在 240 mA 附近获得 4.7% 的最大 WPE，输出功率为 170 mW。在 50°C 和 90°C 时，最大 WPE 仍分别为 2.9% 和 0.8%。迄今为止，由于我们的高材料质量和优化的反射面涂层，低阈值 DFB-QCL 的这些值仍然非常高。认为通过考虑涂层效应优化选择激光腔长度可以进一步提高WPE。

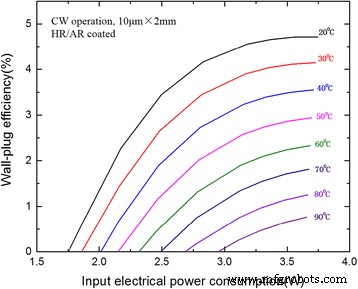
作为 2 毫米长 HR 和 AR 涂层 DFB-QCL 的电功率耗散函数的壁插效率

结论

我们已经在 λ 处展示了单模 DFB-QCL 的室温连续波操作 ~ 4.76 μm。通过在正面沉积由双层电介质 Al2O3 和 Ge 组成的增透膜，成功实现了在所有电流和温度条件下都没有任何模式跳跃的稳定单模。在 20 °C 时，观察到 CW 输出功率高达 170 mW，阈值电流密度非常低，仅为 0.65 kA/cm ² .这种器件代表了在中红外光谱范围内将 DFB-QCLs 稳定的单模操作用于实际应用的重要一步。

缩写

AR：

抗反射

BH：

埋藏异质结构

CW：

连续波

DFB：

分布式反馈

人力资源：

高反射

MBE：

分子束外延

MOVPE：

金属有机气相外延

偏微分方程：

偏微分方程

PECVD：

等离子体增强化学气相沉积

P -我 -V ：

电源-电流-电压

QCL：

量子级联激光器

短信：

边模抑制比

V 次：

阈值电压

WPE：

插墙效率

λ /4 附注：

四分之一波相移