使用由 Rashba 自旋轨道耦合引起的硅烯双线缺陷的可控谷极化

介绍

硅烯是一种低屈曲的单层蜂窝状硅原子晶格，是石墨烯用于谷电子学应用的潜在有吸引力的替代品。低屈曲结构在硅烯中产生了相对较大的自旋轨道耦合 (SOC)，在狄拉克点 K 处估计有大约 1.55 meV 的相当大的能隙 和 K ^′ [1] 与石墨烯不同，硅烯的低能量色散关系是抛物线形式而不是线性形式。借助屈曲结构，可以通过施加电场来控制硅烯的能带结构，甚至可能发生从量子自旋霍尔绝缘体到量子谷霍尔绝缘体的拓扑相变[2, 3]。硅烯已成功地在Ag(111)、Ir(111)和ZrB2(0001)等基材表面合成[4-6]，其独立的稳定结构也已在多项理论研究中得到预测[7] ]。最重要的是，已经成功地通过实验观察到了室温硅烯场效应晶体管（FET）[8]。电场可调性和与现有硅基器件的兼容性使硅烯成为有潜力应用于下一代谷电子学的二维材料。

在石墨烯和过渡金属二硫属化物（MoS2等）等二维（2D）材料中，具有不同晶体取向的材料的两个畴之间的晶界是实​​现谷极化的理想选择，并引起了相当大的关注[9-14 ]。最近，根据第一性原理计算[15, 16]，广泛研究了硅烯中的扩展线缺陷（ELD），发现5-5-8 ELD（以下简称“线缺陷”）是最稳定和最容易形成的结构。从理论上研究了硅烯线缺陷的自旋和谷极化[17-19]。线缺陷的形成可以可视化为两个 Si 晶粒的锯齿形边缘的缝合吸附的硅原子，其中线缺陷的任一侧表现出类似伪边缘状态的行为，锯齿形边缘的晶界作为伪边缘[16]。显然，这种晶格相对于线具有镜像对称性缺陷和被缺陷分隔的“左”和“右”域中相应的晶格向量是相反的[10, 11]。在这种具有反转域边界的线缺陷中，A /B 跨越缺陷时交换子晶格和谷指数。对于石墨烯中的准粒子，线缺陷是半透明的，并且以高入射角出现高谷极化。谷极化为q 是 （电子沿 y 的群速度 方向）依赖于线缺陷。对于具有线性色散和恒定群速度的石墨烯，谷极化在大|q时可以达到接近100% 是 | （对应于高入射角）而随着 |q 而减小 是 |递减并消失为 |q 是 |∼0 [9, 14]。相比之下，硅烯具有两种不同的传输特性 [17, 18]：首先，由于抛物线色散关系，费米能量接近带边缘，因此两个谷变得难以区分；其次，由于螺旋线，传输受到限制。线缺陷两侧的边缘状态反向流动，如图 1c 所示。自然地，在特定 RSOC 中具有 SOC 的系统是高效自旋 FET 的有希望的候选者。 RSOC 产生平面内有效磁场并感应垂直于约束平面注入的自旋进动。自旋极化[20]和反转[21]已在门控硅烯纳米带中进行了研究。理论计算表明，RSOC 可以显着调节硅烯的能带 [22, 23]。例如，在相对较强的 RSOC 下，K 处的自旋向下 (-up) 带 (K ^′ ) 谷值向上移动，而导带中的其他自旋带保持不变。考虑到硅烯线缺陷特有的传输特性和硅烯中RSOC的影响，产生谷极化载流子的实用全电方案变得可行。

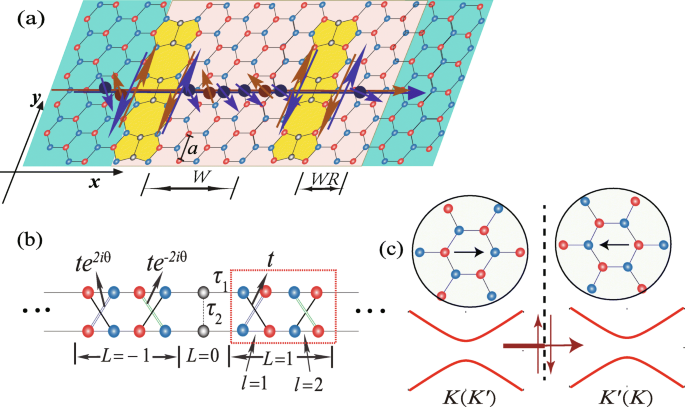
一 状态进动过程示意图 (K ,↑ )（红色球体）和 (K ^′ ,↓ )（蓝色球体）穿过具有两个平行线缺陷的硅片，其中蓝色（红色）圆圈表示 A (B ) 子格。状态 (K ,↑ ) 和 (K ^′ ,↓ ) 沿伪边缘循环，假设 RSOC 和电场存在于法国灰色区域。 W (W =2) 和 WR (写 =1) 以\(\sqrt {3}a\) 为单位表示散射区域的宽度。 b 具有线缺陷的无限硅的简化晶格模型，其中 θ =k 是 一 虚线矩形对应一个超胞。在晶胞中，格点由一组索引指定 (L,l ）。 c K 中一种自旋态的传输 (K ^′ ) 具有反转域边界的跨线缺陷谷。插图显示了由线缺陷（虚线）分隔的两个域中晶格的取向。粗/细线表示由于螺旋边缘状态沿伪边缘反向流动，传输通过线缺陷受到限制

在本文中，我们提出了一种使用硅烯双线缺陷极化不同谷的狄拉克费米子的有效方法，从而利用硅烯中的电场产生明显的谷极化。我们的结果表明，当费米能量接近导带底部时，只要 RSOC 超过本征 SOC，来自两个谷的传输系数的振荡图像（包括宽振荡峰和最低点）就会重合，而仅存在单线缺陷不能分散依赖于谷的电子。当涉及两个平行线缺陷时，振荡的最低点演化为零传输平台，通过垂直电场改变两个狄拉克谷的振荡周期，可以实现对依赖于谷的输运的有效调制，其中振荡周期为两个波谷的增减导致在宽峰零平台对应区域出现完美的波谷极化。在实验中，可以通过测量电导随电场的变化来检测这种纯谷电流。这种现象为利用RSOC和电场有效调节硅烯器件中的谷极化提供了不同的途径。

方法

让我们从两端硅烯线缺陷器件的示意图开始，如图 1a 所示，其中说明了自旋进动以产生由于 RSOC 和电场而产生的谷极化电流。假设RSOC存在于宽度W的线缺陷的一侧 和 WR 以 \(\sqrt {3}a\) 为单位，其中 a =3.86 Å 是原始硅烯的晶格常数，如图 1a 所示。当费米能量位于导带底部时，状态 (K ,↓ )[ (K ,↓ ) 对应于 K 谷中的一个状态 ↓ （向下）旋转] 和 (K ^′ ,↑ ) 由于操纵来自 RSOC 的能带而处于差距中。另外两个状态，(K ,↑ ) 和 (K ^′ ,↓ )，由于 SOC[24] 的自旋动量锁定特性，沿伪边缘循环，如图 1a 所示。对于确定的自旋状态，它沿着线缺陷两侧相反方向的伪边缘流动，可以作为过滤器并限制穿过线缺陷的传输，如图1c所示。

用紧束缚表示中的格模型来描述具有RSOC的线缺陷系统[17, 22]

其中 \(c_{i\alpha }^{\dag }\) 和 \(c_{i_{y}\alpha,\gamma /\delta }^{\dag }\) 表示自旋 α 在硅胶位点 i 和线缺陷，分别是 〈〉/〈〈〉〉 运行在所有最近的/下一个最近的邻居跳跃站点上。前三项表示最近邻跳跃和参数 t ,τ 1、τ 图 2 表示紧束缚模型中的各种最近邻跳跃能量，如图 1b 所示。第四项是具有跳跃参数t的有效SOC 所以 , 和 ν ij =±1 表示相对于正 z 在下一个最近的相邻站点之间逆时针（顺时针）跳跃 -轴。一项理论研究 [16] 表明，缺陷区中两个最近的 Si 原子与原始区中的那些 Si 原子相对相同，并且所有 Si 原子都保留在 sp ² -sp ³ 杂交状态。因此，设置τ是合理的 2=τ 1=t .在第五项中，Δ z 是由垂直于硅片的电场产生的交错亚晶格电势，μ 我 A =±1 (B ） 地点。最后一项表示外在 RSOC 项，其中 t R 是 Rashba 自旋轨道跳跃参数。 d ij 是从站点 j 指向的单位向量 i , 和 \(\vec {\sigma }=(\sigma ^{x},\sigma ^{y},\sigma ^{z})\) 在方程中。 1 是实数自旋泡利矩阵的向量。 RSOC 由电门、金属原子吸附或基底 [20, 25] 施加的外部电位产生，这可以显着破坏硅烯的结构反转对称性。值得注意的是，源自电场的外在 RSOC 被忽略，因为它非常弱。

硅的 ELD 如图 1a 所示，沿着 y 极大地延伸 方向。晶格结构沿 y 的平移对称性 方向表示 k 是 是一个守恒量，根据傅立叶变换（忽略自旋指数）[17]，创建（湮灭）算子可以改写如下：

然后，方程中的哈密顿矩阵。 1 解耦为 \(H=\sum _{k_{y}}H_{k_{y}}\)，其中 \(H_{k_{y}}\) 可以用以下形式描述：

其中 \(\varphi _{i,l}^{\dag }=\left [ c_{{{k}_{y}},i,l,A\uparrow }^{\dag }, c_{{{ k}_{y}},i,l,A\downarrow }^{\dag }, c_{{{k}_{y}},i,l,B\uparrow }^{\dag },c_{ {{k}_{y}},i,l,B\downarrow }^{\dag }\right ]\), i 在索引集 (i,l ) 表示超胞的位置 \((\bar {i}=-i)\)，而 l =1 或 2 表示超晶胞中不同的锯齿形链，如图 1b 中的虚线矩形所示。 \(\hat {T_{ll'}}\) 表示每个锯齿形链的哈密顿矩阵 (l =l ^′ ) 在一个超胞或不同锯齿链之间的相互作用 (l ≠l ^′ ).

注意到两个谷 K 和 K ^′ 现在投射在 [0,±π /3a ] 由于插入了线缺陷。 η的传输矩阵 (η =K /K ^′ ) 谷值使用广义兰道尔公式计算[26, 27],

哪里

和

这里，\(-Im\Sigma _{L,R}=-\left (\Sigma _{L,R}^{r}-\Sigma _{L,R}^{a}\right)/ 2i\ ) 是具有明确矩阵平方根的半正定矩阵，其中 \(\Sigma _{L,R}^{a}=\left [\Sigma _{L,R}^{r}\right ]^{ \dag }\) 是左/右引线的滞后/超前自能。 16×16 子矩阵 G ^r 是延迟格林函数，它沿着 x 连接第一个和最后一个超级单元 方向，可以使用递归格林函数方法计算。 η的总透射系数 谷是 \(T_{\eta }=T^{\uparrow \uparrow }_{\eta }+T^{\uparrow \downarrow }_{\eta }+ T^{\downarrow \uparrow }_{\eta }+T^{\downarrow \downarrow }_{\eta }\) 和自旋极化 P s 和谷极化P η 可以通过

结果与讨论

在计算依赖于自旋的透射系数时，我们设置 τ 2=τ 1=t =1 作为能量单位，SOC强度t 所以 =0.005t , 和费米能量 E f =1.001t 所以 ，位于导带底部。散射区的宽度为W 单线缺陷=1000，两个平行线缺陷还考虑了附加宽度WR=1000，如图1a所示。

图 2 描绘了谷值 \(\eta, T^{sc}_{\eta }/T^{sf}_{\eta }\) 的自旋守恒/自旋翻转传输系数，作为事件的函数角度α (a) 和 RSOC 强度 t R (b-d)。图 2a-c 对应于单线缺陷的情况，（d）是两个平行线缺陷的情况。结果表明，在一个确定的 t R （例如，t R =5t 所以 如图 2a)，由于抛物线色散关系，与自旋相关的透射系数 \(T^{sc}_{K}/T^{sf}_{K}\) 是常数并且与入射角无关，如图 2a 所示。因此，在下面的计算中，我们可以使用入射角α =0 为例。对于弱t R ，由于 Rashba 分裂，出现类似于二维电子气 [26, 27] 的振荡现象，如图 2b 的插图所示。作为 t R 增加 (t R>t 所以 ), \(T_{K}^{\uparrow \uparrow }\) 和 \(T_{K}^{\uparrow \downarrow }\) 与 t R 其中包含一些振荡峰值和最低点，而 \(T_{K}^{\downarrow \downarrow }/T_{K}^{\downarrow \uparrow }\) 趋于零，因为费米能量位于其间隙中，如如图2b所示。因此，K的总透射系数 谷主要由自旋向上状态贡献。实际上，两个谷的振荡图像，K 和 K ^′ , 同时 K 的透射系数 ^′ 谷主要由自旋向下的电子贡献。

<图片>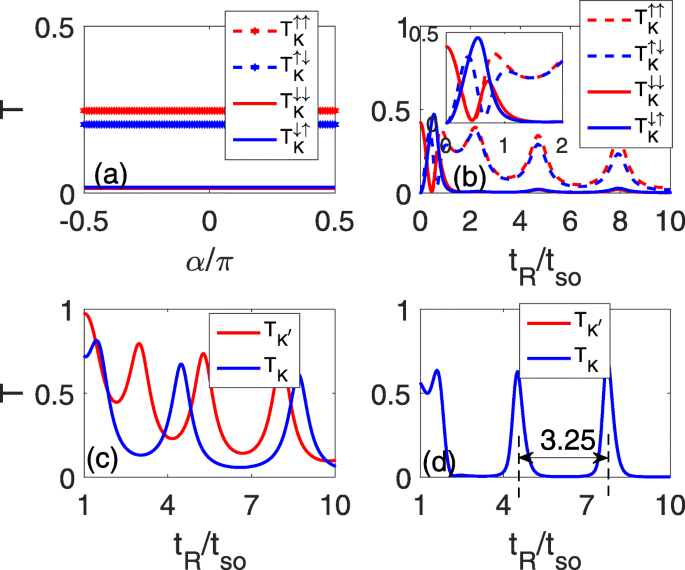

作为入射角函数的自旋守恒和自旋翻转传输系数 α 在 t R =5t 所以 在 a 并作为 RSOC 强度的函数 t R 在 b –d , 其中 a -c 用于单线缺陷和 d 对于两个平行线缺陷，Δ z =0.2t 所以 在 c

在垂直电场的存在下，谷简并被解除，两个谷的振荡行为不同：K的振荡周期 谷值增加，而 K ^′ 谷值减小，如图 2c 所示。然而，由于振荡的最低点具有确定的幅度，因此仅用单个线缺陷过滤一个锥形谷状态似乎是不可行的。自然地，可以考虑具有两个平行线缺陷的振荡现象来进一步抑制传输，如图2d所示。比较图 2b 和 d 可以看出，振荡峰值变得窄而尖锐，而振荡最低点变宽和减弱，形成了零传输平台。两个相邻振荡峰值之间的间隔固定在 3.25t 所以 ，如图2d中两条虚线所示。

为了达到更好的谷值滤波效果，我们将注意力集中在垂直电场的效果上。这种效应的结果如图 3 所示。如上所述，两个谷的振荡周期以相反的方式变化，图 2d 中原始重叠的振荡峰值得到缓解。同时，零传输平台对于 T 变宽和变窄 K 和 \(T_{K^{\prime }}\)，分别如图 3a 和 b 所示。在 Δ z =0.15t 所以 , 两个相邻振荡峰之间的间隔发展为 3.6t 所以 对于 T K , 而它减少到 3.1t 所以 对于 \(T_{K^{\prime }}\)，如图 3a 中的两条蓝色和红色虚线所示。随着电场的增强，两个相邻振荡峰之间的距离继续增加/减少 T K /\(T_{K^{\prime }}\)，即 5.4t 所以 /2.8t 所以 在 Δ z =0.3t 所以 ，如图 3b 所示。振荡周期的变化将导致相应的宽峰零平台区域，其中 P 完美的谷极化 η 可以实现 =±1 个平台，如图 3c 和 d 所示。同时，高自旋极化P s 当 P 时也会出现 η =±1.

<图片>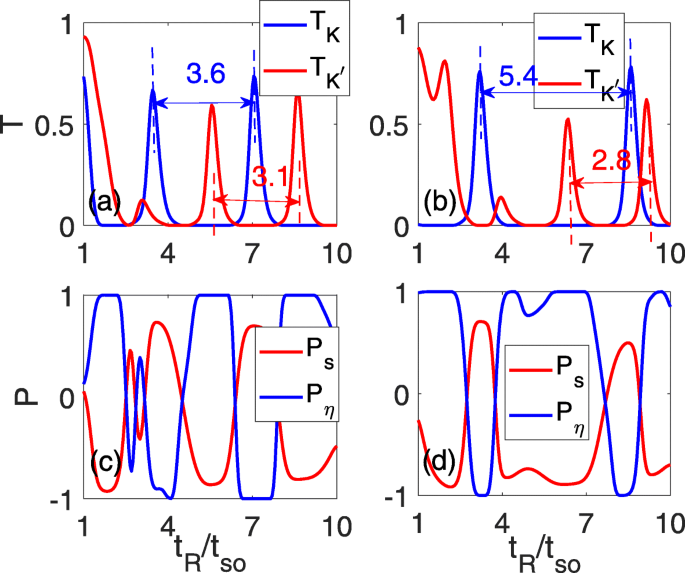

总透射系数 \(T_{K}/T_{K^{\prime }}\) (a , b ) 和自旋/谷极化 (c , d ) 作为 RSOC 强度的函数 t R 对于不同的亚晶格势。 Δ z =0.15t 所以 在 a 和 c 和Δ z =0.3t 所以 在 b 和 d;其他参数与图2d相同

然而，由于 RSOC 的不可控性，即使在线缺陷中感应的 RSOC 可能大于固有 SOC，仍然难以通过实验检测到这种纯谷电流。为了方便地通过实验探测纯谷电流，我们还研究了传输系数和谷极化作为电场的函数，可以在实验过程中连续控制。结果表明，具有 P 的完美谷极化 η =±1 可以在Δ的一定范围内出现 z 并且它可以从 P 改变 η =1 到 P η =-1 随着电场的增加，如图 4a 所示。对于确定的 t R （例如 t R =7.2t 所以 ，如图 4a) 中的虚线所示，透射系数 \(T_{K}/T_{K^{\prime }}\) 随 Δ 振荡 z ，其中 K 的宽传输峰值 (K ^′ ) 谷对应于 K 的零传输平台 ^′ (K ) 谷。随着电场的变化，总透射系数基本上由一个谷贡献，完美的谷极化总是可以发生在\(T_{K}/T_{K^{\prime }}\)的最大值附近，如图所示图 4b。随着费米能量离开能带边缘，即使在 E 下，完美的谷极化仍然存在 f =1.5t 所以 ，其中可以很好地保持平稳关系，如图 4c 所示。在实验过程中，人们可以用实验可测量的量（如电导）分析从左到右引线的谷极化电流，该量与总传输系数成正比。两个最小值（有时为零）之间的最大电导应该来自一个谷。我们可以根据公式 \(G=\frac {e^{2}}{h}\int _{-k_{F}}^{k_{F}}T\frac {dk_ {y}}{2\pi /L_{y}}=\frac {e^{2}}{h}\frac {Ly\sqrt {E^{2}-t^{2}_{so}} }{2\pi \hbar v_{F}}2T\) [28]，其中 L 是 =2a ≈7.72Å 是硅烯线缺陷的宽度，v F =5.5×10 ⁵ 米 /s 是费米速度，\(\hbar =h/2\pi \) 是约化的普朗克常数 \(\phantom {\dot {i}\!}h=4.13566743\times 10^{-15}eV\cdot s, T=T_{K}+T_{K'}\) 为总透射系数，E 是入射电子的现场能量。然后，电导约为 \(G\approx \left [0.7T\sqrt {E^{2}-t^{2}_{so}}/eV\right ]\frac {e^{2}}{ H}\）。还发现随着入射侧的现场能量升高到E =0.15t (t =1.6eV )，由于自旋和动量守恒，两个谷的传输系数与图4c相比变化很小，传输峰值-零平台关系保持不变，如图4d所示。在这种情况下，电导约为 \(G\approx 0.17T\frac {e^{2}}{h}\)，这是相当大的并且可以在实验中检测到。观察这种现象的能量窗口约为 0.5t 所以 (t 所以 <E <1.5t 所以 ) 与 t 成正比 所以 .在实验中，控制带边附近的费米能量并不困难，通过接近Bi(111)双层[29]，SOC间隙甚至可以从根本上提高到44 meV，可以大大提高能量区域以检测纯谷电流。此外，该计算模型也适用于石墨烯、锗烯[30]、stanene和MoS2[31-36]的其他低屈曲对应物，它们具有更大的带隙[37, 38]以及SOC强度（ stanene 的 SOC 强度可以达到 0.1eV[38, 39])。在实际实验中，通过特殊基板打破面内镜像对称性，很容易实现可以超过固有SOC的强RSOC[40]。因此，该方案在实验中完全可行。

<图片>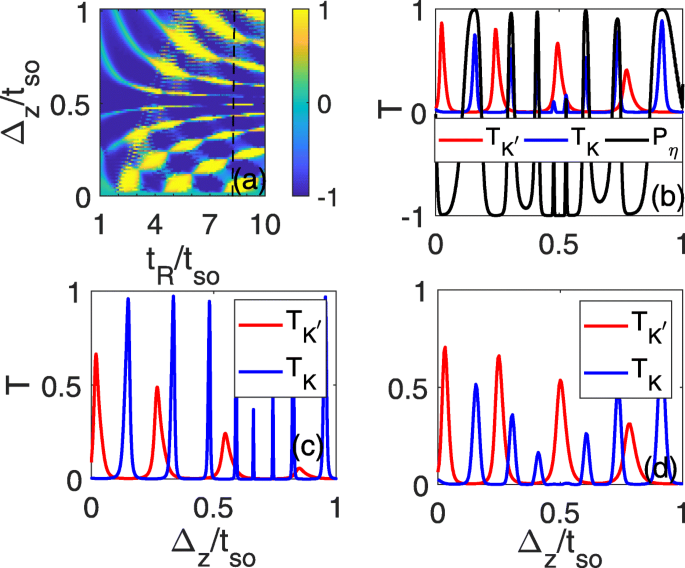

谷极化a 和 \(T_{K}/T_{K^{\prime }}\) (b –d ) 作为 Δ 的函数 z 和 t R . t R =7.2t 所以 在 (b –d ), E f =1.5t 所以 在 c 和 d , 现场能量为 E =0.15t 在 d 的左电极中;所有其他参数与图2d中的相同