德摩根定理
一位名叫 DeMorgan 的数学家开发了一对关于布尔代数中群互补的重要规则。
按组 互补,我指的是一组术语的互补,用长条表示超过一个变量。
您应该回忆一下逻辑门章节,将所有输入反转到一个门会将门的基本功能从 AND 反转为 OR,反之亦然,并且还反转输出。
因此,所有输入反相的或门(负或门)的行为与与非门相同,所有输入反相的与门(负与门)的行为与或非门相同。
DeMorgan 的定理以“反向”形式陈述了相同的等价性:反转任何门的输出会导致与具有反转输入的相反类型的门(AND 与 OR)具有相同的功能:
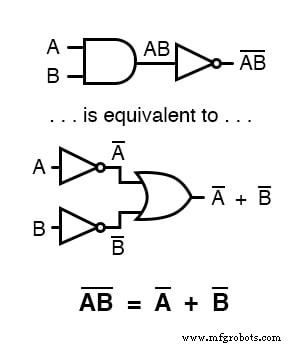
在 AB 项上延伸的长条充当分组符号,因此与 A 和 B 独立倒置的乘积完全不同。
换句话说,(AB)' 不等于 A'B'。因为“素数”符号 (') 不能像条形一样延伸到两个变量上,所以我们不得不使用括号使其适用于前一句中的整个术语 AB。
然而,当一个条形拉伸超过一个变量时,它会充当它自己的分组符号。
正如我们将看到的,这对布尔表达式的求值和简化方式产生了深远的影响。
德摩根定理
DeMorgan 定理可能被认为是 break 长条形符号。
当一个长条被破坏时,直接在中断之下的操作从加法变为乘法,反之亦然,并且被破坏的条块保留在各个变量上。举例说明:
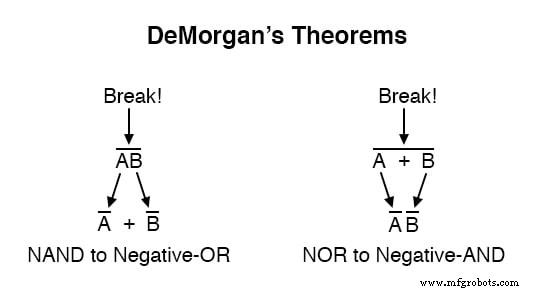
当表达式中存在多个条形“层”时,您一次只能破坏一个条形 ,并且通常通过首先打破最长(最上面)的条形来开始简化。
为了说明这一点,让我们采用表达式 (A + (BC)')' 并使用 DeMorgan 定理简化它:
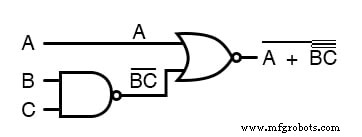
按照首先断开最长(最上面)条的建议,我将首先断开覆盖整个表达式的条:

结果,原来的电路简化为A输入反相的三输入与门:
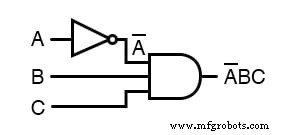
你不应该永远 在一个步骤中打破多个柱线,如下所示:
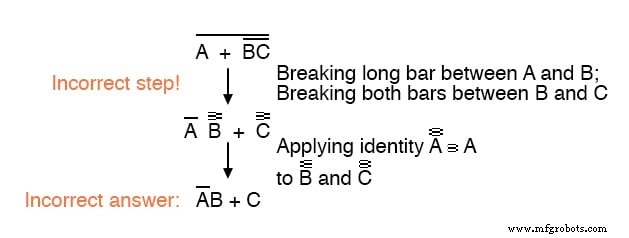
尽管节省步骤并一次打破多个小节可能很诱人,但通常会导致错误的结果,所以不要这样做!
可以通过先断开短柱而不是先断开长柱来适当地减少此表达式:
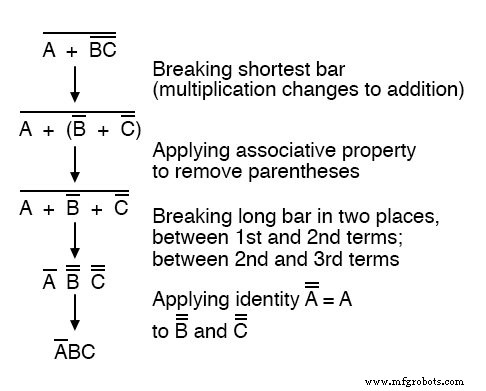
最终结果是相同的,但与使用第一种方法(最长的柱线首先被打破)相比,需要更多的步骤。
注意在第三步中我们是如何在两个地方打破长条的。
这是一种合法的数学运算,与一步打破两根柱不同!
禁止在一个步骤中打破多个条形是不是 禁止在多个地方打破酒吧。
闯入多个地方 一步就可以了;打破多个条 一步也不是。
您可能想知道为什么要在子表达式 B' + C' 周围放置括号,考虑到我在下一步中刚刚删除了它们。
我这样做是为了强调德摩根定理的一个重要但容易被忽视的方面。
由于长条形用作分组符号,以前由断开的条形分组的变量必须保持分组,以免丢失适当的优先级(操作顺序)。
在这个例子中,如果我在打破短线后忘记加上括号真的没有关系,但在其他情况下可能会。
考虑这个例子,从一个不同的表达式开始:
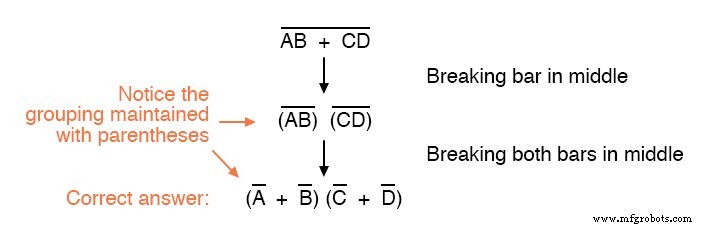
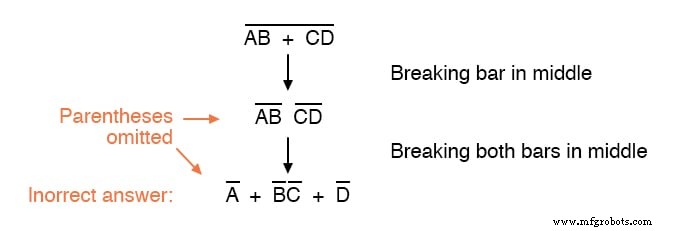
如您所见,保持此表达式的补码所暗示的分组对于获得正确答案至关重要。
让我们将 DeMorgan 定理的原理应用于门电路的简化:
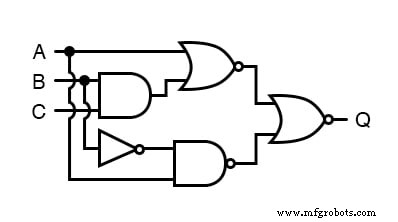
与往常一样,我们简化此电路的第一步必须是生成等效的布尔表达式。
我们可以通过在每个门的输出处放置一个子表达式标签来做到这一点,因为输入变得已知。这是此过程的第一步:
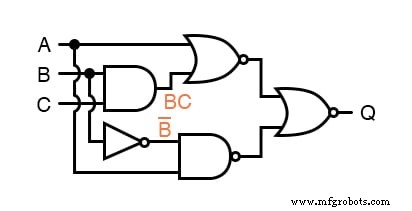
接下来,我们可以标记第一个或非门和与非门的输出。
在处理反向输出门时,我发现在没有 的情况下为门的输出编写表达式更容易 最后的反转,箭头指向反转气泡之前。
然后,在引出大门的电线处(在气泡之后),我写下了完整的补充表达式。
这有助于确保我不会忘记子表达式中的补充条,强制自己将表达式编写任务分为两个步骤:
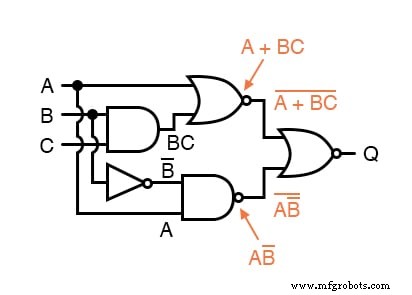
最后,我们为最后一个 NOR 门写一个表达式(或一对表达式):
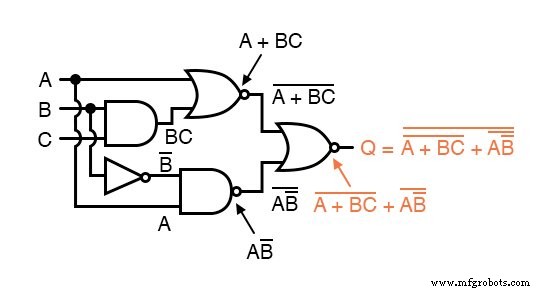
现在,我们使用布尔代数的恒等式、性质、规则和定理(DeMorgan 的)来简化这个表达式:
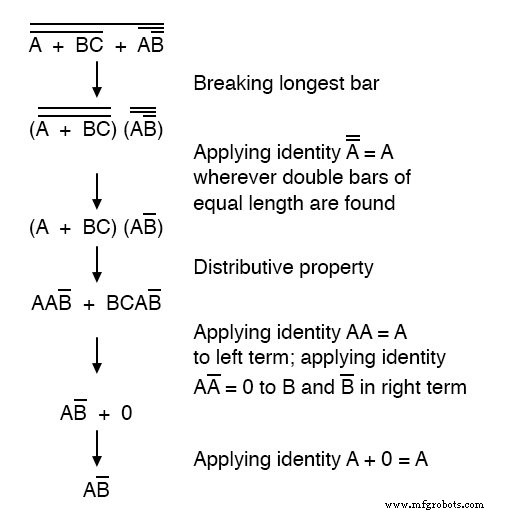
这个大大简化的表达式的等效门电路如下:
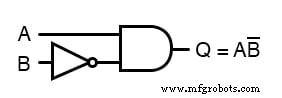
评论:
- 德摩根定理描述了具有反向输入的门和具有反向输出的门之间的等价性。简单地说,与非门相当于负或门,或非门相当于负与门。
- 当“断开”布尔表达式中的补码时,位于换行下方的运算(加法或乘法)会反转,并且断开的条部分保留在相应的项上。
- 在打破最长的(最上面的)条形之前,先打破它下面的任何条形,通常更容易解决问题。你必须永远不要 尝试一步打破两个小节!
- 补充条用作分组符号。因此,当一个条被打破时,它下面的术语必须保持分组。括号可以放在这些分组的术语周围,以帮助避免更改优先级。
相关工作表:
- 布尔代数工作表
工业技术


