将真值表转换为布尔表达式

在设计数字电路时，设计人员通常从描述电路应该做什么的真值表开始。

设计任务主要是确定哪种类型的电路将执行真值表中描述的功能。

虽然有些人似乎天生就有能力查看真值表并立即设想任务所需的逻辑门或继电器逻辑电路，但我们其他人可以使用程序技术。

在这里，布尔代数以最引人注目的方式证明了它的实用性。

为了说明这种程序方法，我们应该从一个现实的设计问题开始。

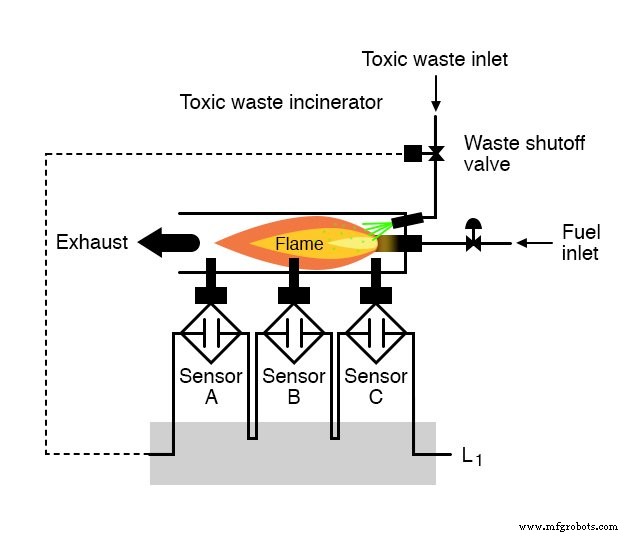
假设我们的任务是为有毒废物焚化炉设计火焰检测电路。

火的强烈热量旨在中和进入焚化炉的废物的毒性。

这种基于燃烧的技术通常用于中和可能感染致命病毒或细菌的医疗废物：

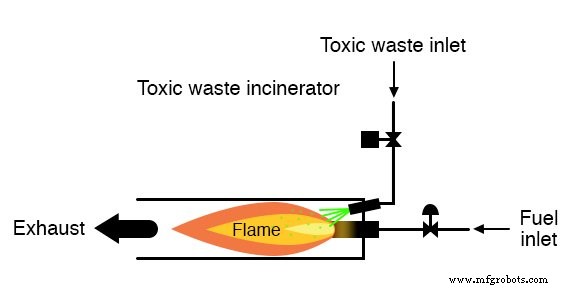
只要焚烧炉中保持火焰，就可以安全地将废物注入其中进行中和。

然而，如果火焰要熄灭，继续将废物注入燃烧室是不安全的，因为它会在未中和的情况下离开排气，并对靠近排气的任何人构成健康威胁。

我们在这个系统中需要的是一种可靠的方法来检测火焰的存在，并且只有在火焰检测系统“证明”火焰存在的情况下才允许注入废物。

存在几种不同的火焰检测技术：光学（检测光）、热（检测高温）和导电（检测火焰路径中的电离粒子），每一种技术都有其独特的优点和缺点。

假设由于潜在地将未中和的废物从该焚化炉的排气中排出所涉及的高度危险，决定使火焰检测系统变得多余（多个传感器），以便单个传感器的故障不会导致把一排毒气排出体外。

每个传感器都配备了一个常开触点（如果没有火焰则打开，如果检测到火焰则关闭），我们将用它来激活逻辑系统的输入：

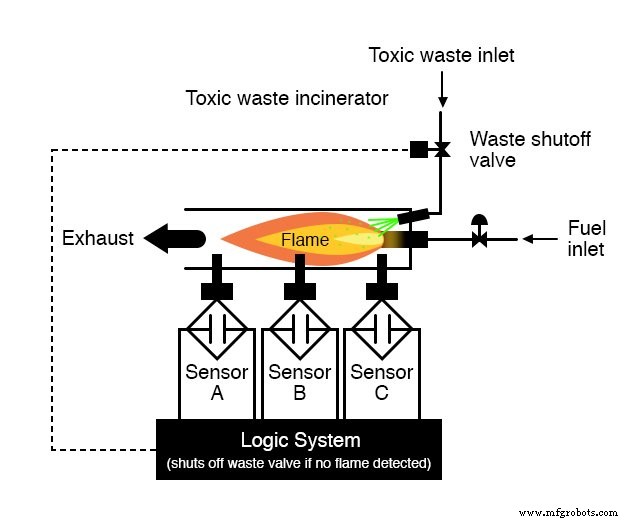
我们现在的任务是设计逻辑系统的电路，当且仅当传感器证明火焰良好时才能打开废物阀。

不过，首先，我们必须决定这个控制系统的逻辑行为应该是什么。

如果三个传感器中只有一个检测到火焰，我们是否希望阀门打开？可能不会，因为这会违背拥有多个传感器的目的。

如果任何一个传感器发生故障，以致在没有火焰时错误地指示存在火焰，则基于“三个传感器中的任何一个显示火焰”原理的逻辑系统将给出相同的输出单传感器系统也会出现同样的故障。

更好的解决方案是设计系统，当且仅当所有三个传感器时命令阀门打开 检测良好的火焰。

这样，任何错误显示火焰的单个故障传感器都无法将阀门保持在打开位置；相反，它需要所有三个传感器都以相同的方式发生故障——这是一种极不可能发生的情况——才会发生这种危险情况。

因此，我们的真值表将如下所示：

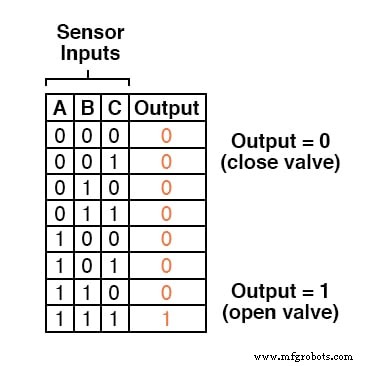
不需要太多洞察力就可以使用三输入与门生成此功能：当且仅当输入 A AND 时，电路的输出才会为“高” 输入 B AND 输入C都是“高”：

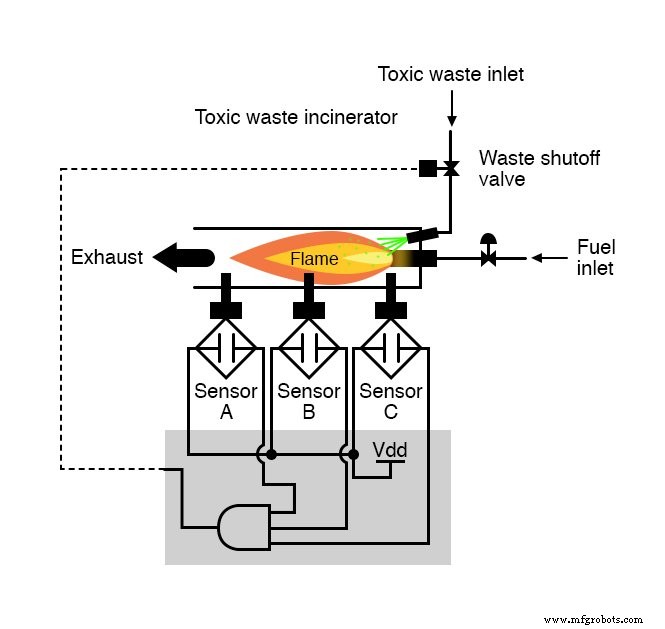
如果使用继电器电路，我们可以通过串联三个继电器触点来创建此 AND 功能，或者简单地串联三个传感器触点，以便发送电力以打开废液阀的唯一方法是所有三个传感器指示火焰：

虽然这种设计策略最大限度地提高了安全性，但它使系统非常容易受到相反类型的传感器故障的影响。

假设三个传感器中的一个出现故障，当焚烧炉的燃烧室中确实有良好的火焰时，它会指示没有火焰。

单个故障会不必要地关闭废物阀，导致生产时间损失和燃料浪费（助长未用于焚烧废物的火）。

如果有一个逻辑系统允许这种故障而不会不必要地关闭系统，但仍然提供传感器冗余，以便在任何单个传感器“高”故障（始终显示火焰）的情况下保持安全，这将是很好的，无论是否有一个要检测）。

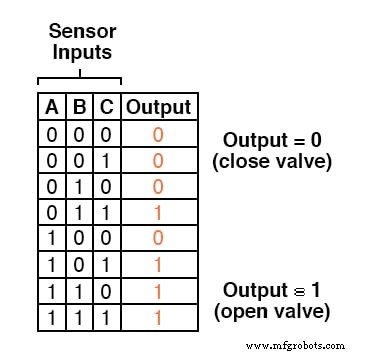
满足这两种需求的策略是“三分之二”的传感器逻辑，如果三个传感器中至少有两个显示良好的火焰，则废物阀打开。

这种系统的真值表如下所示：

使用乘积总和

在这里，什么样的逻辑电路才能满足真值表并不一定很明显。

然而，在称为乘积之和的布尔表达式的标准形式中可以找到一种设计这种电路的简单方法。 , 或 SOP ， 形式。

正如您可能怀疑的那样，Sum-Of-Products 布尔表达式实际上是一组添加的布尔项（summed ) 在一起，每一项都是乘法 (product ) 布尔变量的组合。

SOP 表达式的一个例子是这样的：ABC + BC + DF，乘积“ABC”、“BC”和“DF”的总和。

Sum-Of-Products 表达式很容易从真值表中生成。

我们所要做的就是检查输出为“高”(1) 的任何行的真值表，并编写一个布尔乘积项，在给定这些输入条件的情况下等于值 1。

例如，在我们的三取二逻辑系统真值表的第四行中，其中 A=0、B=1 和 C=1，乘积项将是 A'BC，因为该项当且仅当 A=0、B=1 和 C=1 时，其值为 1：

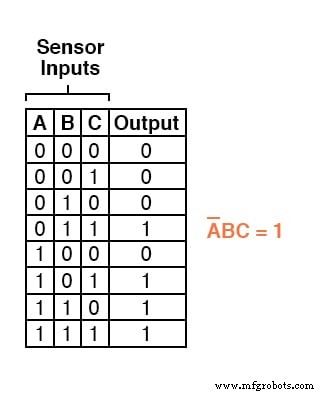
真值表的其他三行的输出值为 1，因此这些行也需要布尔乘积表达式来表示它们：

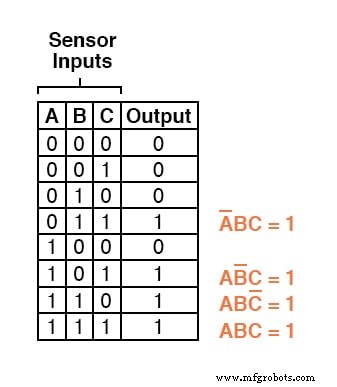
最后，我们通过加法将这四个布尔乘积表达式连接在一起，以创建一个单一的布尔表达式来描述整个真值表：

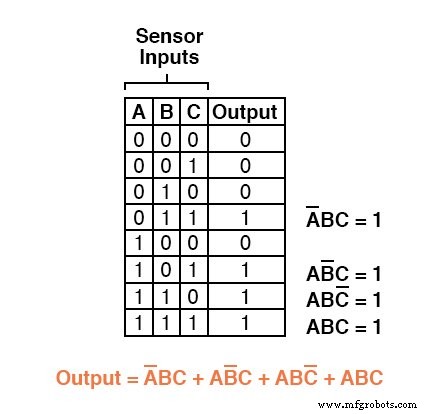
现在我们有了真值表函数的布尔积和表达式，我们可以根据该表达式轻松设计逻辑门或继电器逻辑电路：

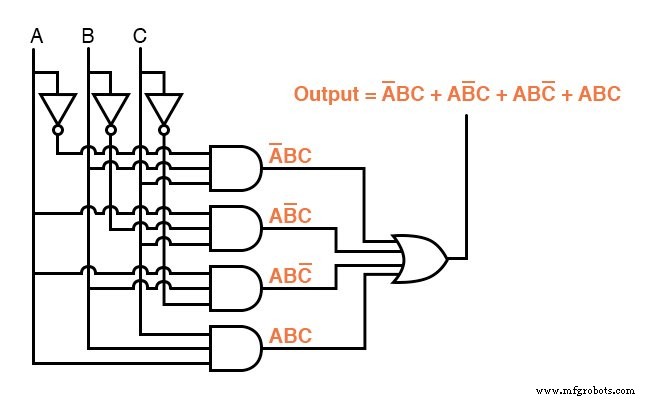
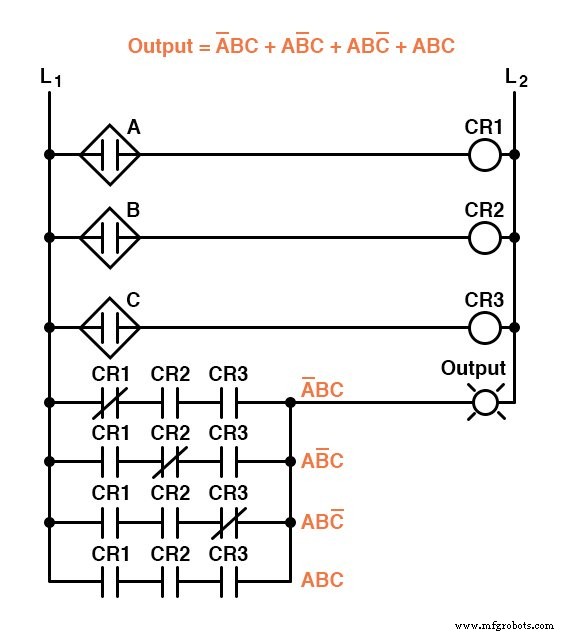
不幸的是，这两个电路都非常复杂，可以从简化中受益。

使用布尔代数技术，可以显着简化表达式：

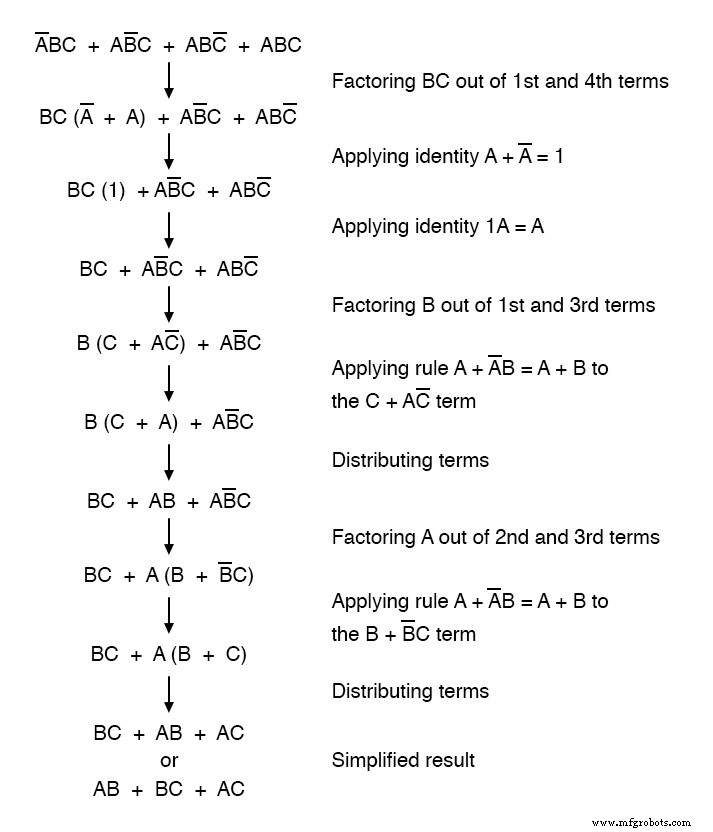
由于简化，我们现在可以构建更简单的逻辑电路，以门或继电器形式执行相同的功能：

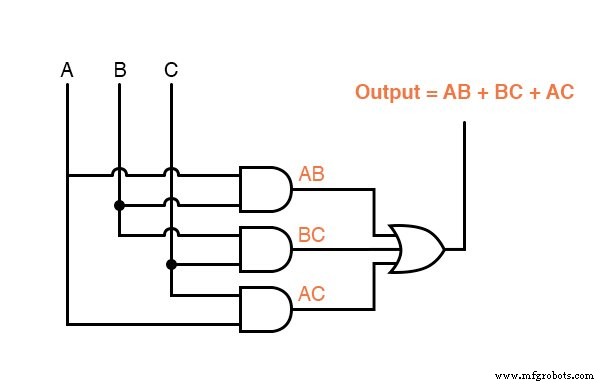
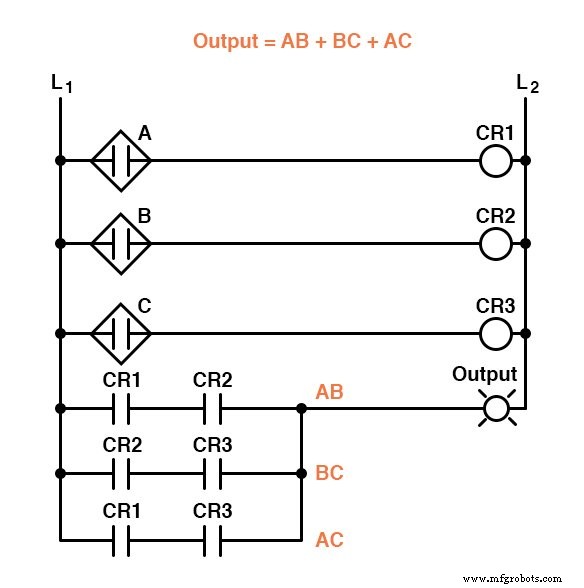
根据来自三个火焰传感器中的两个的火焰验证，这些电路中的任何一个都可以充分执行操作焚化炉废物阀的任务。

至少，这是我们拥有一个安全的焚化炉系统所需要的。

但是，我们可以通过添加逻辑电路来扩展系统的功能，该逻辑电路旨在检测任何一个传感器是否与其他两个传感器不一致。

如果所有三个传感器都正常工作，它们应该以相同的精度检测火焰。

因此，它们应该全部记录为“低”（000：无火焰）或全部记录为“高”（111：良好的火焰）。

任何其他输出组合（001、010、011、100、101 或 110）构成传感器之间的不一致，因此可能作为潜在传感器故障的指示器。

如果我们添加电路来检测六种“传感器不一致”条件中的任何一种，我们就可以使用该电路的输出来激活警报。

监控焚化炉的任何人都会做出判断，要么继续使用可能发生故障的传感器（输入：011、101 或 110）运行，要么关闭焚化炉以确保绝对安全。

此外，如果焚化炉关闭（无火焰），并且一个或多个传感器仍指示有火焰（001、010、011、100、101 或 110），而其他（多个）传感器指示无火焰，就知道是传感器有问题了。

设计这种“传感器不一致”检测电路的第一步是编写描述其行为的真值表。

既然我们已经有了一个真值表来描述“好火焰”逻辑电路的输出，我们可以简单地在表中添加另一个输出列来表示第二个电路，并制作一个表示整个逻辑系统的表：

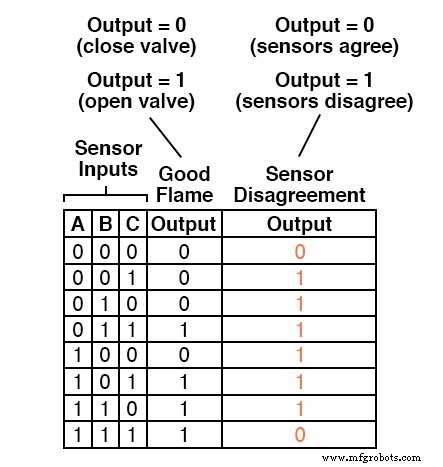
虽然可以为这个新的真值表列生成 Sum-Of-Products 表达式，但它需要六个项，每个项包含三个变量！

这样的布尔表达式需要很多步骤来简化，而且很可能会出现代数错误：

使用总和积

生成 Sum-Of-Products 表达式以说明真值表中所有“高”(1) 输出条件的替代方法是生成 Product-Of-Sums , 或 POS , 表达式, 来解释所有“低” (0) 输出条件。

由于最后一个真值表列中“低”输出的实例要少得多，因此生成的 Product-Of-Sums 表达式应该包含更少的项。

顾名思义，Product-Of-Sums 表达式是一组添加的项（sums ), 乘以 (product ) 在一起。

POS 表达式的一个示例是 (A + B)(C + D)，即“A + B”和“C + D”之和的乘积。

首先，我们确定最后一个真值表列中哪些行具有“低”(0) 输出，并编写一个布尔求和项，对于该行的输入条件等于 0。

例如，在真值表的第一行中，其中 A=0、B=0 和 C=0，总和项将为 (A + B + C)，因为如果且该项的值为 0仅当 A=0、B=0 和 C=0 时：

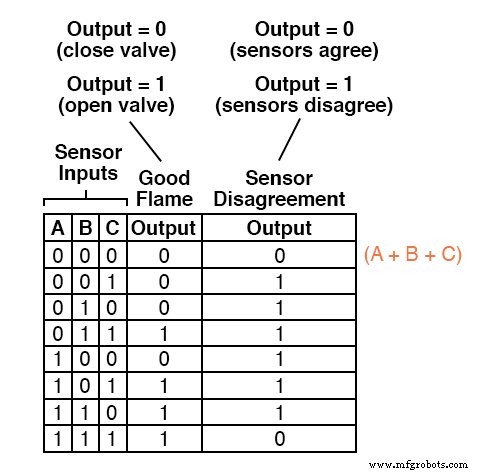
最后一个真值表列中只有另一行具有“低”(0) 输出，因此我们需要的只是一个求和项来完成我们的求和表达式。

最后一个求和项表示输入条件为 A=1、B=1 和 C=1 的 0 输出。

因此，该项必须写为 (A' + B'+ C')，因为只有 补码的 仅对于该条件，输入变量将等于 0：

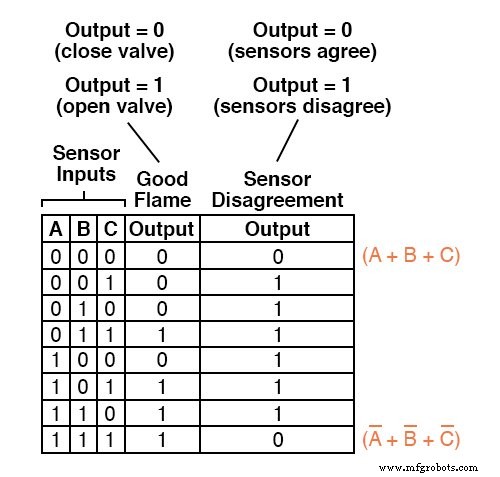
完整的 Product-Of-Sums 表达式当然是这两个求和项的乘法组合：

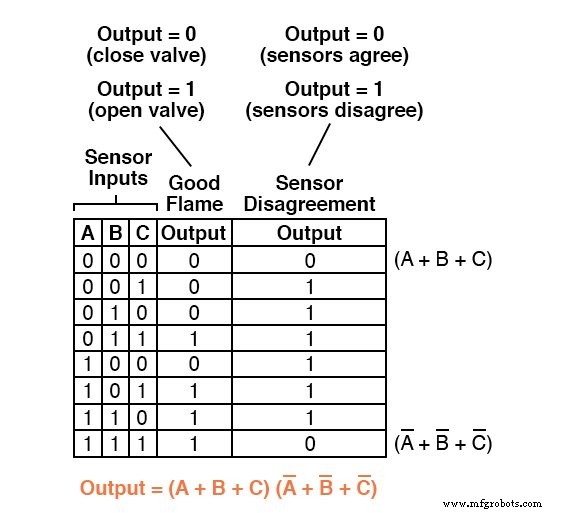
虽然 Sum-Of-Products 表达式可以以一组 AND 门的形式实现，它们的输出连接到单个 OR 门，但 Product-Of-Sums 表达式可以实现为一组 OR 门馈入单个与门：

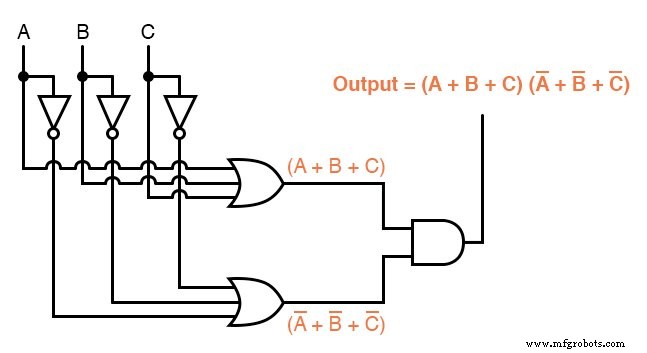
相应地，Sum-Of-Products 表达式可以实现为串联继电器触点的并联集合，而 Product-Of-Sums 表达式可以实现为并联继电器触点的串联集合：

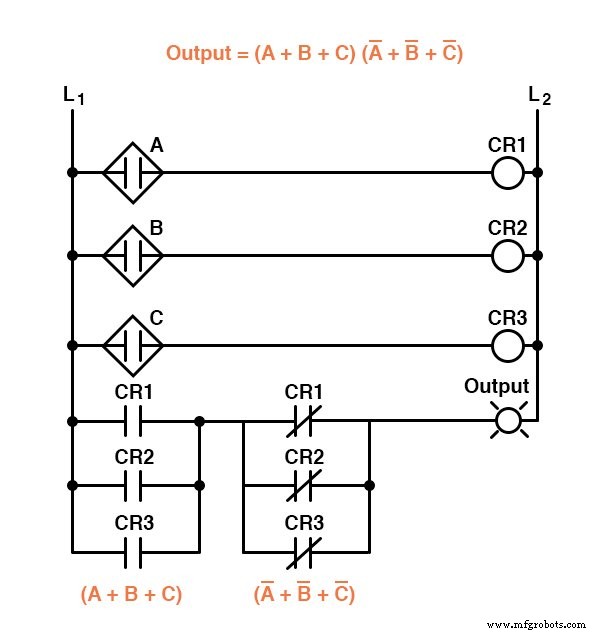
前两个电路仅代表“传感器不一致”逻辑电路的不同版本，而不是“良好火焰”检测电路。

整个逻辑系统将是“良好火焰”和“传感器不一致”电路的组合，显示在同一张图上。

在可编程逻辑控制器 (PLC) 中实现，整个逻辑系统可能类似于这样：

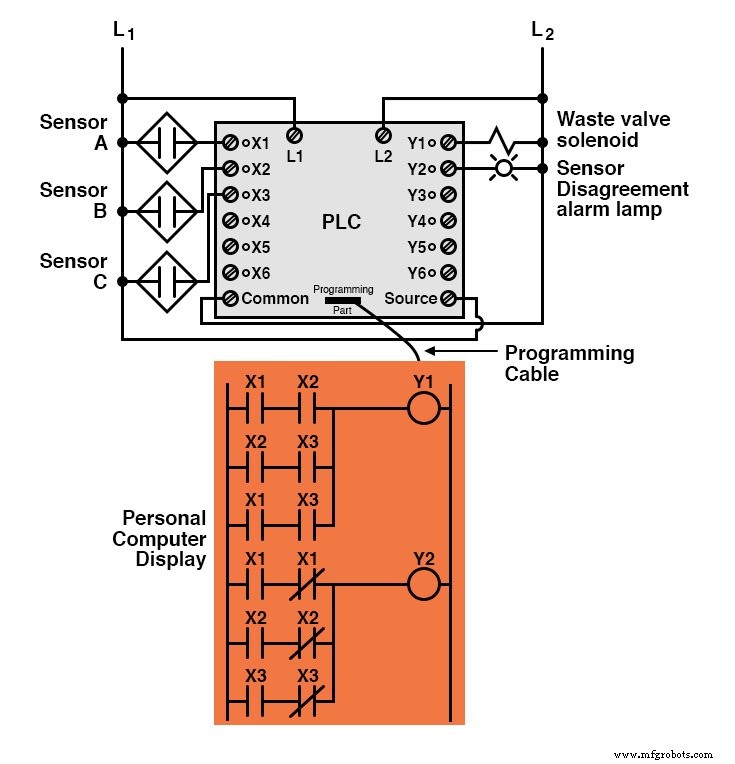
如您所见，当应用于真值表时，Sum-Of-Products 和 Products-Of-Sums 标准布尔形式都是强大的工具。

它们使我们能够从真值表中推导出布尔表达式——最终是一个实际的逻辑电路，真值表是我们希望逻辑电路做什么的书面规范。

能够使用简单的确定性程序将书面规范转化为实际电路意味着可以实现数字电路设计过程的自动化。

换句话说，可以对计算机进行编程以根据真值表规范设计自定义逻辑电路！

从真值表到最终电路的步骤是如此明确和直接，以至于几乎不需要创造力或其他原创思想来执行它们。

评论：

• 产品总和 , 或 SOP ，布尔表达式可以很容易地从真值表中生成，方法是确定表的哪些行的输出为 1，为每一行写一个乘积项，最后对所有乘积项求和。这将创建一个表示整个真值表的布尔表达式。
• Sum-Of-Products 表达式非常适合作为一组 AND 门（产品）输入单个 OR 门（和）来实现。
• 总和积 , 或 POS ，布尔表达式也可以很容易地从真值表中生成，通过确定表的哪些行的输出为 0，为每一行写一个和项，最后将所有和项相乘。这将创建一个表示整个真值表的布尔表达式。
• Product-Of-Sums 表达式非常适合作为一组 OR 门（和）输入到单个 AND 门（产品）中。

相关工作表：

• 乘积和乘积表达式工作表
• 布尔代数工作表