全加法

半加器非常有用，直到您想要添加一个以上的二进制数字量。开发两个二进制数字加法器的缓慢方法是制作一个真值表并减少它。然后当你决定做一个三位二进制加法器时，再做一次。然后当你决定做一个四位加法器时，再做一次。那么当......电路会很快，但开发时间会很慢。

查看两个二进制数字和显示我们需要将加法扩展到多个二进制数字。

<前> 11 11 11 --- 110

查看中间列使用了多少个输入。我们的加法器需要三个输入； a、b 和前一个和的进位，我们可以使用我们的两输入加法器构建一个三输入加法器。

Σ 是容易的部分。普通算术告诉我们，如果 Σ =a + b + Cin 和 Σ1 =a + b，那么 Σ =Σ1 + Cin。

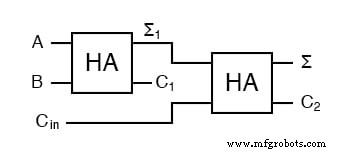
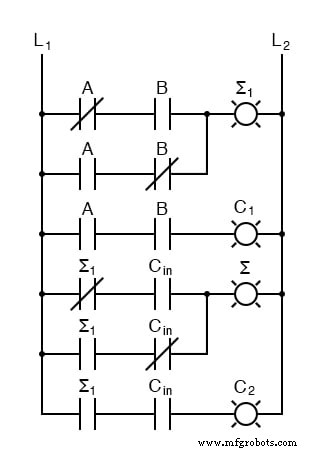
我们如何处理 C1 和 C2？让我们看一下三个输入和并快速计算：

Cin + a + b =? 0 + 0 + 0 =0 0 + 0 + 1 =1 0 + 1 + 0 =1 0 + 1 + 1 =10 1 + 0 + 0 =1 1 + 0 + 1 =10 1 + 1 + 0 =10 1 + 1 + 1 =11 

如果您对低位有任何疑问，请确认电路和梯形图计算正确。

为了计算高位，请注意当 a + b 产生 C1 时，在两种情况下它都是 1。此外，当 a + b 产生 Σ1 且 Cin 为 1 时，高位为 1。因此，当 C1 OR (Σ1 AND Cin) 时，我们将有一个进位。我们完整的三输入加法器是：

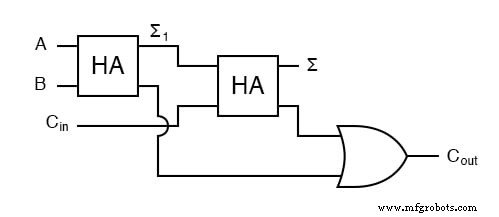
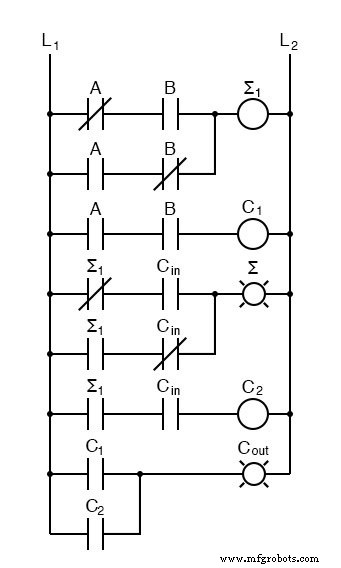
对于某些设计，能够消除一种或多种类型的门可能很重要，您可以在不改变结果的情况下用异或门替换最终的或门。

我们现在可以连接两个加法器来添加 2 位数量。

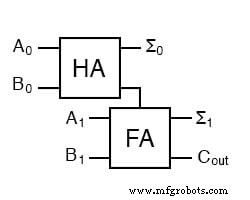
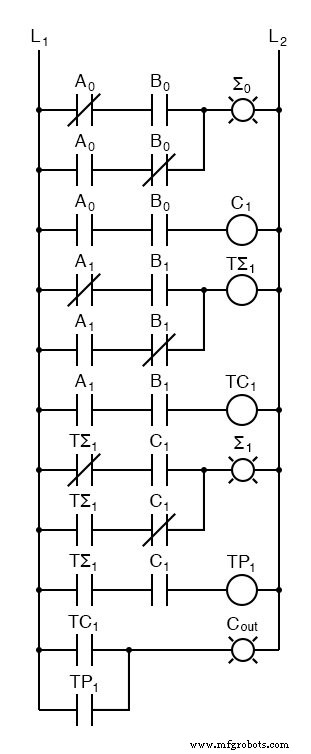
A0为A的低位，A1为A的高位，B0为B的低位，B1为B的高位，Σ0为和的低位，Σ1为高位总和的位，Cout 是进位。

永远不会以这种方式制作两位二进制数字加法器。相反，最低位也将通过全加器。

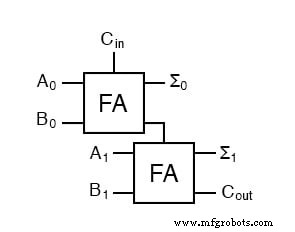
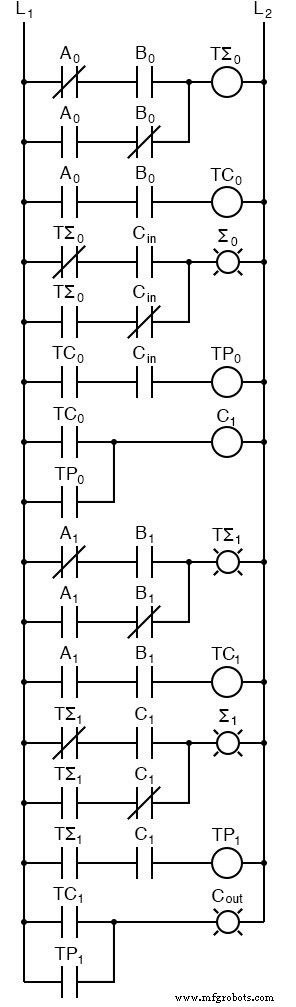
这有几个原因，一个是我们可以允许电路确定最低阶进位是否应包含在总和中。这允许链接更大的总和。考虑两种不同的方式来查看四位和。

<前> 111 1<-+ 11<+- 0110 | 01 | 10 1011 | 10 | 11 ----- - | ---- | --- 10001 1 +-100 +-101

如果我们允许程序添加一个两位数并记住进位以备后用，然后在下一次求和中使用该进位，即使我们只提供了一个两位加法器，程序也可以添加用户想要的任意数量的位。小型 PLC 也可以链接在一起以获得更大的数量。

这些全加器还可以扩展到空间允许的任意位数。例如，这里是如何做一个 8 位加法器。

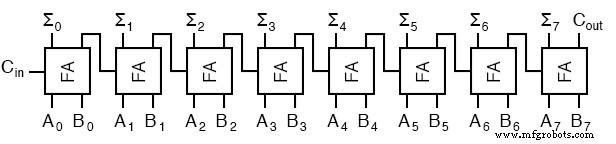
这与使用两个2位加法器组成一个4位加法器，然后使用两个4位加法器组成一个8位加法器或重新复制梯形逻辑并更新数字的结果相同。

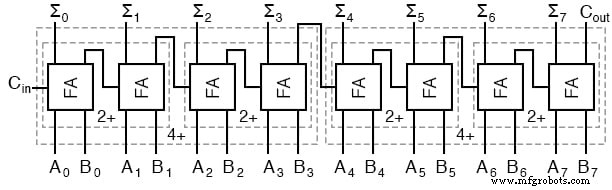
每个“2+”是一个 2 位加法器，由两个全加器组成。每个“4+”是一个 4 位加法器，由两个 2 位加法器组成。两个 4 位加法器的结果就是我们使用全加器构建的同一个 8 位加法器。

对于任何大型组合电路，通常有两种设计方法：您可以采用更简单的电路并复制它们；或者您可以将复杂的电路设计为一个完整的设备。使用更简单的电路来构建复杂的电路可以让您花更少的时间设计，但需要更多的时间让信号通过晶体管传播。

上面的 8 位加法器设计要等待所有的 Cx 输出信号从 A0 + B0 向上移动到 Σ7 的输入。如果设计人员将一个 8 位加法器构建为一个完整的设备，简化为乘积之和，那么每个信号只通过一个非门、一个与门和一个或门。

17 个输入设备有一个真值表，其中包含 131,072 个条目，将 131,072 个条目减少为乘积之和需要一些时间。在设计具有最大允许响应时间以提供最终结果的系统时，您可以从使用更简单的电路开始，然后尝试替换电路中太慢的部分。

这样您就可以将大部分时间花在电路中重要的部分上。

相关工作表：

• 二元数学电路工作表