有限状态机
到目前为止,所呈现的每个电路都是一个组合 电路。这意味着其输出仅取决于其当前输入。该类型电路的先前输入对输出没有影响。
然而,有许多应用需要我们的电路具有“记忆”;记住以前的输入并根据它们计算它们的输出。输出不仅取决于当前输入而且取决于输入历史的电路称为顺序电路 .
在本节中,我们将学习如何设计和构建这样的时序电路。为了了解这个过程是如何工作的,我们将使用一个例子来研究我们的主题。
因此,假设我们有一个数字问答游戏,可以在时钟上运行并从手动按钮读取输入。但是,我们希望开关只向电路传输一个高电平脉冲。如果我们将按钮直接挂在游戏电路上,它将在我们手指所能达到的尽可能少的时钟周期内传输高电平。在一个常见的时钟频率上,我们的手指永远都不够快。
设计过程具有必须遵循的特定步骤才能完成工作:
第 1 步
设计过程的第一步是用简单但清晰的词来定义我们希望我们的电路做什么:
“我们的任务是设计一个次级电路,当手动按钮被按下时,它会传输一个持续时间只有一个周期的高脉冲,并且在按钮被按下并再次按下之前不会传输另一个脉冲。” em>
第 2 步
下一步是设计状态图。
这是一个由圆圈和箭头组成的图表,直观地描述了我们电路的操作。在数学方面,这个描述时序电路操作的图是一个有限状态机。请注意,这是一个摩尔有限状态机。
它的输出只是它当前状态的函数,而不是它的输入。这与 Mealy 有限状态机形成对比,其中输入影响输出。在本教程中,将只研究摩尔有限状态机。
我们电路的状态图如下:(下图)
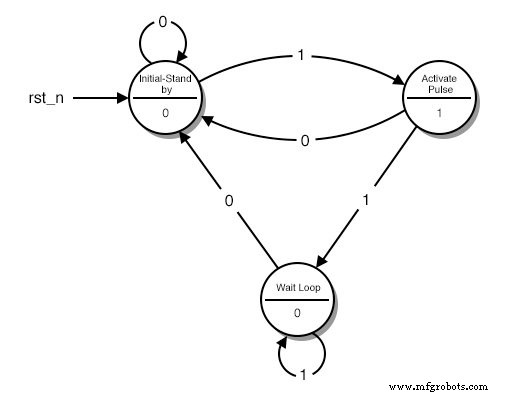
状态图
每个圆圈代表一个“状态”,一个可以找到我们的机器的明确定义的条件。在圆圈的上半部分,我们描述了这种情况。描述有助于我们记住我们的电路在那种情况下应该做什么。
- 第一个圆圈是“待机”状态。这是我们的电路开始的地方,它等待另一个按钮按下。
- 第二个圆圈是刚刚按下按钮并且我们的电路需要发送一个高电平脉冲的情况。
- 第三个圆圈是我们的电路在返回“待机”状态之前等待按钮被释放的状态。
圆圈的下部是我们电路的输出。如果我们希望我们的电路在特定状态下传输高电平,我们在该状态上设置 1。否则我们放一个 0。
每个箭头代表从一种状态到另一种状态的“过渡”。每个时钟周期发生一次转换。根据当前的 Input,我们可能每次都进入不同的状态。注意每个箭头中间的数字。这是当前的输入。
例如,当我们处于“初始-待机”状态并“读取”一个 1 时,图表告诉我们必须进入“激活脉冲”状态。如果我们读到 0,我们必须保持“初始待机”状态。
那么,我们的“机器”究竟是做什么的呢?它从“初始 - 待机”状态开始并等待,直到在输入读取 1。然后它进入“激活脉冲”状态并在其输出上传输一个高脉冲。如果按钮一直被按下,则电路进入第三种状态,即“等待循环”。
在那里等待按钮被释放(输入变为 0),同时在输出上传输一个低电平。然后一切重新开始!
这可能是设计过程中最困难的部分,因为它不能用简单的步骤来描述。建立状态图需要经验和一些敏锐的思考,但剩下的只是一组预先确定的步骤。
第 3 步
接下来,我们用 binary 替换描述图表不同状态的词 数字。我们从初始状态分配的 0 开始枚举。然后我们继续枚举我们喜欢的任何状态,直到所有状态都有它们的编号。结果看起来是这样的:(下图)
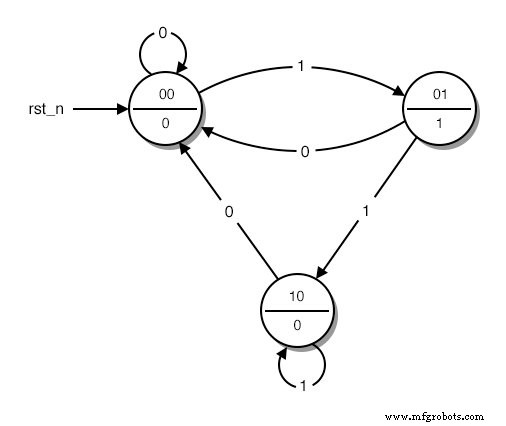
带有编码状态的状态图
第 4 步
之后,我们填写状态表 .该表具有非常特殊的形式。我将给出我们例子的表格,并用它来解释如何填写。(下图)
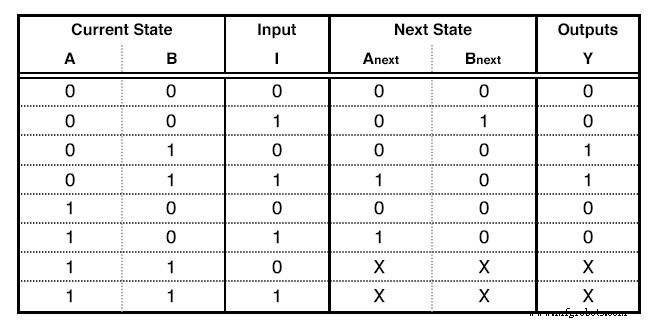
状态表
第一列与我们分配给状态图的最高数字的位数一样多。如果我们有 5 个状态,我们最多可以使用 100,这意味着我们将使用 3 列。对于我们的示例,我们最多使用了数字 10,因此只需要 2 列。这些列描述了当前状态 我们的电路。
在 Current State 列的右侧,我们写了 Input Columns .这些将与我们的输入变量一样多。我们的例子只有一个输入。
接下来,我们编写下一个状态列 .这些与当前状态列一样多。
最后,我们编写输出列 .这些和我们的输出一样多。我们的示例只有一个输出。由于我们构建了更有限状态机,因此输出仅取决于当前输入状态。这就是输出列有两个 1 的原因:产生一个独立于输入 I 的输出布尔函数。继续阅读以获取更多详细信息。当前状态和输入列是我们表的输入。我们用从 0 到的所有二进制数填充它们:
2 (当前状态列数+输入列数) -1
幸运的是,它比听起来简单。通常情况下,状态图中的行会比我们在状态图中创建的实际状态多,但没关系。
Next State 列的每一行都填充如下:我们用我们在状态图中到达的状态填充它,在状态图中,从同一行的当前状态我们跟随同一行的输入。如果必须填写当前状态编号与状态图中的任何实际状态不对应的行,我们用无关项 (X) 填充它。毕竟,我们不在乎我们可以从一个不存在的国家去哪里。我们一开始就不会在那里!同样,它比听起来更简单。
输出列由状态图中对应的当前状态的输出填充。
状态表完成!它像状态图一样完整地描述了我们电路的行为。
步骤 5a
下一步是采用理论上的“机器”并在电路中实现它。大多数情况下,此实现涉及触发器。本指南专门针对此类实施,并将描述 D - 人字拖和 JK - 人字拖的程序。 T - 人字拖将不包括在内,因为它们与前两个案例过于相似。选择要使用的触发器是任意的,通常由成本因素决定。最好的选择是同时进行分析并决定哪种类型的触发器可以实现最少的逻辑门数量和较低的成本。
首先,我们将研究如何使用 D-Flip Flops 实现我们的“机器”。
我们将需要与 State 列一样多的 D - Flip Flops,在我们的示例中为 2。对于每个触发器,我们将在状态表(下图)中添加一列,其中包含触发器输入的名称,在本例中为“D”。对应于每个触发器的列描述了我们必须给触发器什么输入才能从当前状态转到下一个状态 .对于 D - Flip Flop,这很容易:必要的输入等于 Next State。在包含 X 的行中,我们也在此列中填充 X。
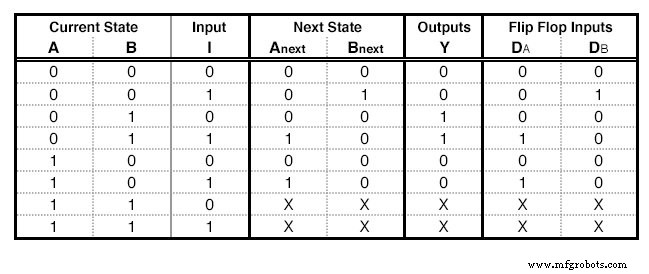
带 D 的状态表 - 触发器激励
步骤 5b
我们可以用 JK - Flip Flops 做同样的步骤。然而,存在一些差异。 JK - 触发器有两个输入,因此我们需要为每个触发器添加两列。每个单元格的内容由JK的激励表决定:

这张表说,如果我们想从状态 Q 到状态 Qnext,我们需要为每个终端使用特定的输入。例如,要从 0 到 1,我们需要用 1 喂给 J 而我们不在乎 我们将哪个输入输入到终端 K。
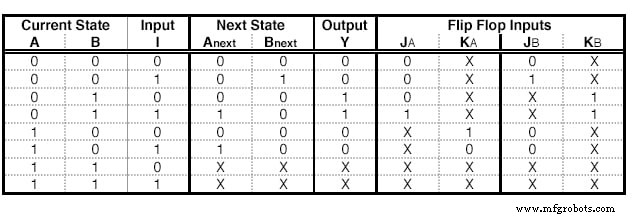
带有 JK 的状态表 - 触发器激励
第 6 步
我们正处于程序的最后阶段。剩下的就是确定产生触发器输入和输出的布尔函数。我们将为我们拥有的每个触发器输入提取一个布尔函数。这可以通过卡诺图来完成。这个地图的输入变量是当前状态变量以及 输入。
也就是说,我们的 D-Flip Flops 的输入函数如下:(下图)
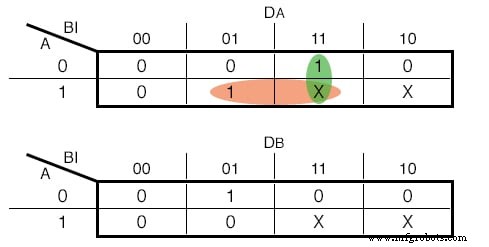
D - 触发器输入的卡诺图
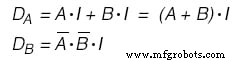
如果我们选择使用JK - Flip Flops,我们的功能如下:(下图)
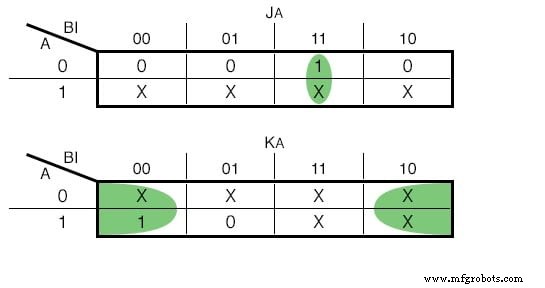
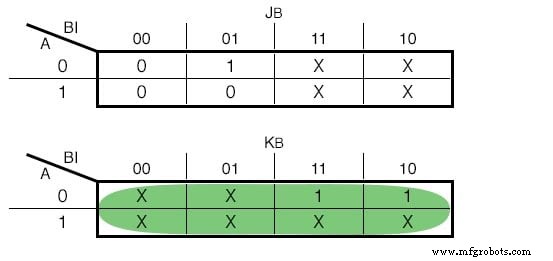
JK 卡诺图 - 触发器输入
卡诺图也将用于确定输出的函数:(下图)
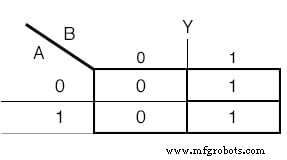
输出变量 Y 的卡诺图
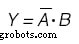
第 7 步
我们设计我们的电路。我们放置触发器并使用逻辑门来形成我们计算的布尔函数。门从触发器的输出和电路的输入获取输入。不要忘记将时钟连接到人字拖!
D-Flip Flop版本:(下图)

完成的 D - Flip Flop 时序电路
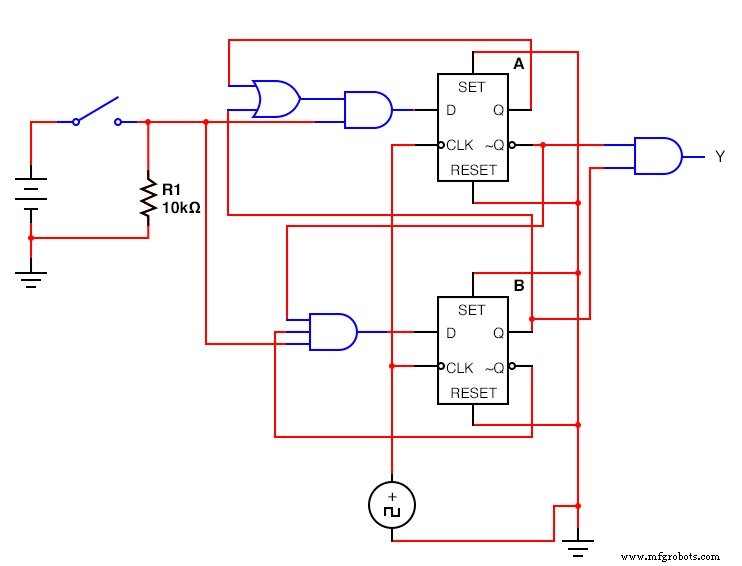
JK-人字拖版本:(下图)
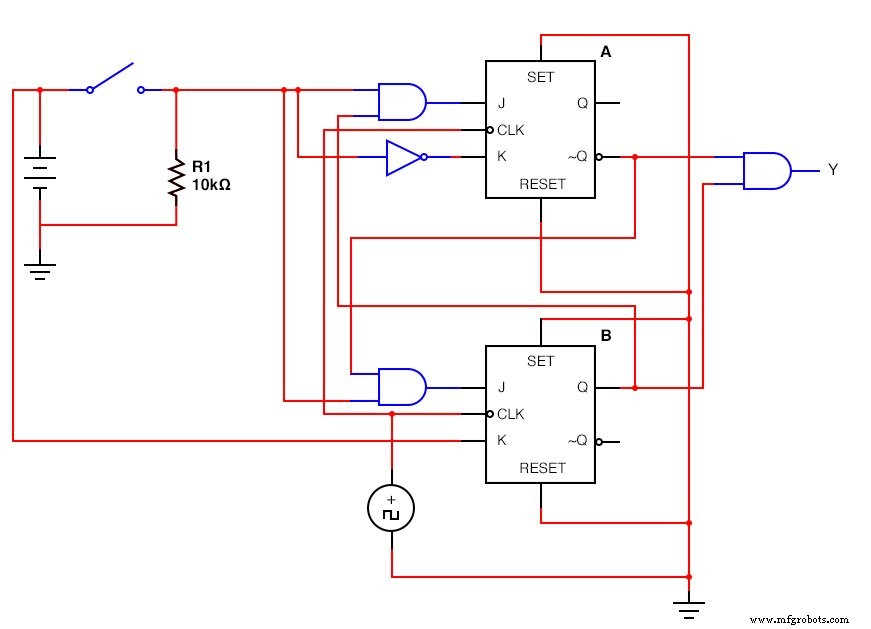
完成的 JK - 触发器顺序电路
就是这个!我们已经成功地设计并构建了一个时序电路。乍一看,这似乎是一项艰巨的任务,但经过练习和重复后,该过程将变得微不足道。时序电路可以作为更大电路的控制部件派上用场,并且可以执行我们能想到的任何时序逻辑任务。天空才是极限! (或至少是电路板)
评论:
- 顺序逻辑函数具有“记忆”功能,并考虑过去的输入以决定输出。
- 有限状态机是时序逻辑函数的抽象数学模型。它具有有限的输入、输出和状态数。
- FSM 通过使用触发器在现实电路中实现
- 实施过程需要特定的步骤顺序(算法)才能执行。
工业技术


