ADC 电路的实际考虑

也许 ADC 最重要的考虑因素是它的分辨率 .分辨率是转换器输出的二进制位数。由于 ADC 电路接收一个连续可变的模拟信号，并将其分解为许多离散步骤中的一个，因此了解这些步骤总共有多少个很重要。

例如，一个 10 位输出的 ADC 最多可以表示 1024 (2 ¹⁰ ) 信号测量的独特条件。在0%到100%的测量范围内，转换器输出的唯一二进制数为1024个（从0000000000到1111111111，含）

11 位 ADC 的输出状态将是其两倍（2048，或 2 ¹¹ )，代表了 0% 到 100% 之间信号测量的独特条件的两倍。

分辨率在数据采集系统（设计用于以电子形式解释和记录物理测量值的电路）中非常重要。假设我们正在使用带有 10 位 ADC 的仪器测量 40 英尺高的储水罐中的水的高度。

水箱中 0 英尺的水对应于测量值的 0%，而水箱中 40 英尺的水对应于测量值的 100%。由于 ADC 固定为 10 位二进制数据输出，因此它会将任何给定的油箱液位解释为 1024 种可能状态中的一种。

确定每个步骤将代表多少物理水位 对于 ADC，我们需要将 40 英尺的测量跨度除以 0 到 1024 可能性范围内的步数，即 1023（比 1024 少一个）。这样做，我们得到了每步 0.039101 英尺的数字。

这相当于每步 0.46921 英寸，略小于 ADC 的每个二进制计数表示的半英寸水位。

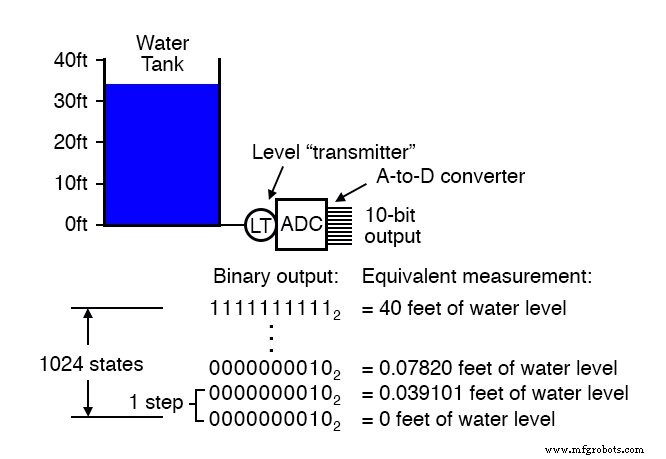
这个 0.039101 英尺（0.46921 英寸）的步长值代表仪器可检测到的最小罐液位变化量。诚然，这是一个很小的数量，不到 40 英尺总测量跨度的 0.1%。

但是，对于某些应用程序，它可能还不够好。假设我们需要该仪器能够指示低至十分之一英寸的油箱液位变化。为了达到这种程度的分辨率并仍然保持 40 英尺的测量跨度，我们需要一个具有 10 个以上 ADC 位的仪器。

要确定需要多少 ADC 位，我们首先需要确定 40 英尺中有多少个 1/10 英寸的步长。答案是 40/(0.1/12) 或 4800 1/10 英寸步长 40 英尺。因此，我们需要足够的位来提供二进制计数序列中至少 4800 个离散步长。

10 位给了我们 1023 步，我们通过计算 2 的 10 次方 (2 ¹⁰ =1024）然后减一。

遵循相同的数学过程，2 ¹¹ -1 =2047, 2 ¹² -1 =4095，和 2 ¹³ -1 =8191。12 位低于 4800 步所需的数量，而 13 位已绰绰有余。因此，我们需要一台分辨率至少为 13 位的仪器。

ADC 电路的另一个重要考虑因素是它的采样频率 ，或转化率 .

这只是转换器输出新二进制数的速度。与分辨率一样，这种考虑与 ADC 的具体应用相关。如果转换器用于测量缓慢变化的信号，例如储水罐中的水位，它可能具有非常慢的采样频率，但仍能正常工作。

相反，如果它用于对每秒数千次循环的音频信号进行数字化，则转换器需要明显更快。考虑以下 ADC 转换率与信号类型的关系图，典型的具有规则采样间隔的逐次逼近 ADC：

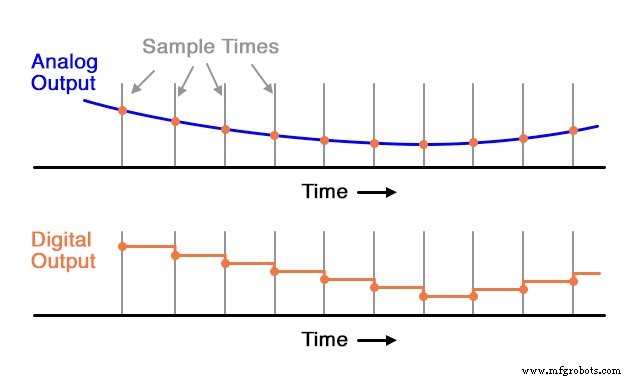
在这里，对于这种缓慢变化的信号，采样率足以捕捉其总体趋势。但是考虑这个 具有相同采样时间的示例：

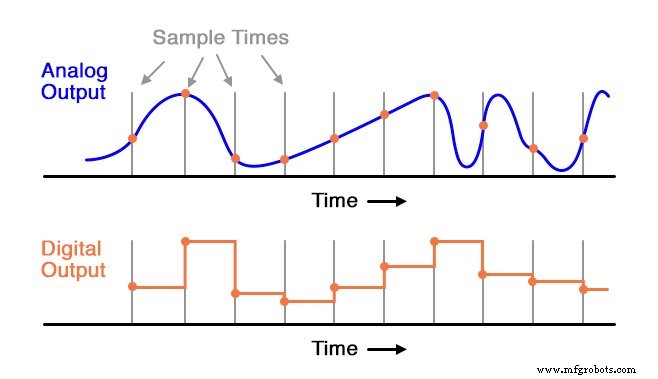
当采样周期太长（太慢）时，模拟信号的大量细节将被遗漏。请注意，尤其是在模拟信号的后半部分，数字输出完全无法再现真实形状。

即使在模拟波形的第一部分，数字再现也明显偏离了波形的真实形状。 ADC 的采样时间必须足够快以捕获模拟波形中的基本变化。

在数据采集术语中，ADC 理论上可以捕获的最高频率波形是所谓的奈奎斯特频率 ，等于 ADC 采样频率的二分之一。因此，如果ADC电路的采样频率为5000Hz，那么它能够成功解析的最高频率波形将是2500Hz的奈奎斯特频率。

如果 ADC 受到频率超过该 ADC 的奈奎斯特频率的模拟输入信号的影响，转换器将输出假低频的数字化信号。这种现象被称为锯齿 .观察下图以了解混叠是如何发生的：

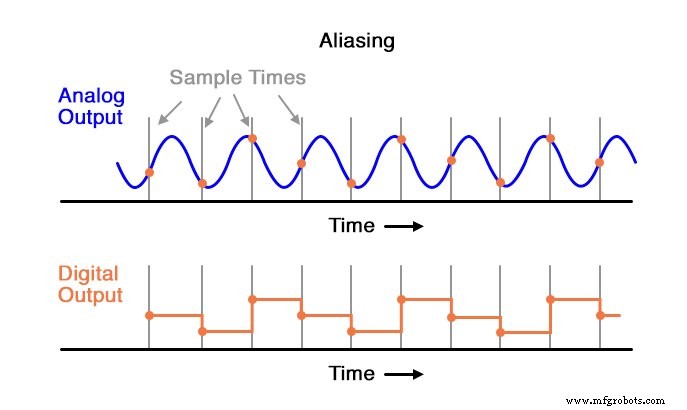
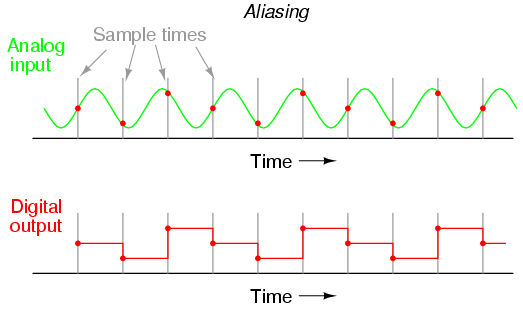
请注意输出波形的周期如何比输入波形的周期长（慢）得多，并且两个波形的形状甚至不相似：

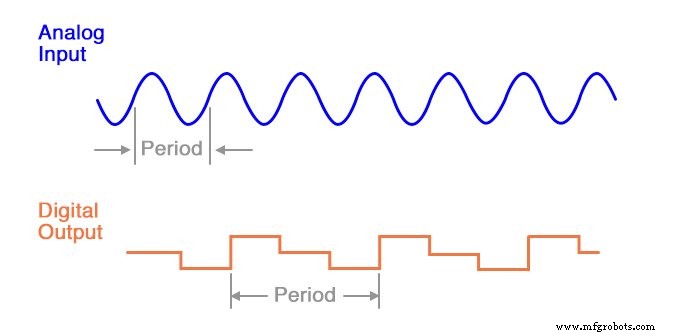
应该理解，奈奎斯特频率是一个绝对 ADC 的最大频率限制，并不代表最高实用 频率可测量。为安全起见，不应期望 ADC 成功解析任何大于其采样频率五分之一到十分之一的频率。

防止混叠的一种实用方法是在 ADC 输入之前放置一个低通滤波器，以阻止任何大于实际限制的信号频率。这样，ADC 电路将不会看到任何过高的频率，因此不会尝试将它们数字化。

通常认为这些频率不转换比让它们“混叠”并作为错误信号出现在输出中更好。

另一种衡量 ADC 性能的方法是阶跃恢复 .这是衡量 ADC 改变其输出以匹配模拟输入的大而突然变化的速度的方法。特别是在某些转炉技术中，阶跃恢复是一个严重的限制。

一个例子是跟踪转换器，它具有典型的快速更新周期，但步长恢复异常缓慢。理想的 ADC 具有非常高的分辨率的大量位，以闪电般的速度采样，并立即从步骤中恢复。不幸的是，它也不存在于现实世界中。

当然，这些特性中的任何一个都可以通过增加电路复杂性来改善，无论是在增加组件数量和/或以更高时钟速度运行的特殊电路设计方面。

但是，不同的 ADC 技术具有不同的优势。以下是从最好到最差的排名摘要：

• 分辨率/复杂度比： 单斜率积分、双斜率积分、计数器、跟踪、逐次逼近、闪光。
• 速度： 闪光、跟踪、逐次逼近、单斜率积分和计数器、双斜率积分。
• 步骤恢复： Flash、逐次逼近、单斜率积分和计数器、双斜率积分、跟踪。请记住，这些不同 ADC 技术的排名取决于其他因素。

例如，ADC 对阶跃恢复的速率如何取决于阶跃变化的性质。跟踪 ADC 对所有阶跃变化的响应同样缓慢，而单斜率或计数器 ADC 记录从高到低的阶跃变化比从低到高的阶跃变化更快。

逐次逼近 ADC 在解析任何模拟信号时几乎同样快，但如果信号的变化慢于每个时钟脉冲的一个分辨率步长，则跟踪 ADC 将始终胜过逐次逼近 ADC。

我认为积分转换器比计数器转换器具有更高的分辨率/复杂度比，但这是假设精密模拟积分器电路的设计和制造复杂度低于计数器转换器中所需的精密 DAC。其他人可能不同意这个假设。