电阻和无功交流电路中的功率

考虑单相交流电源系统的电路，其中 120 伏、60 赫兹交流电压源向电阻负载供电：（下图）

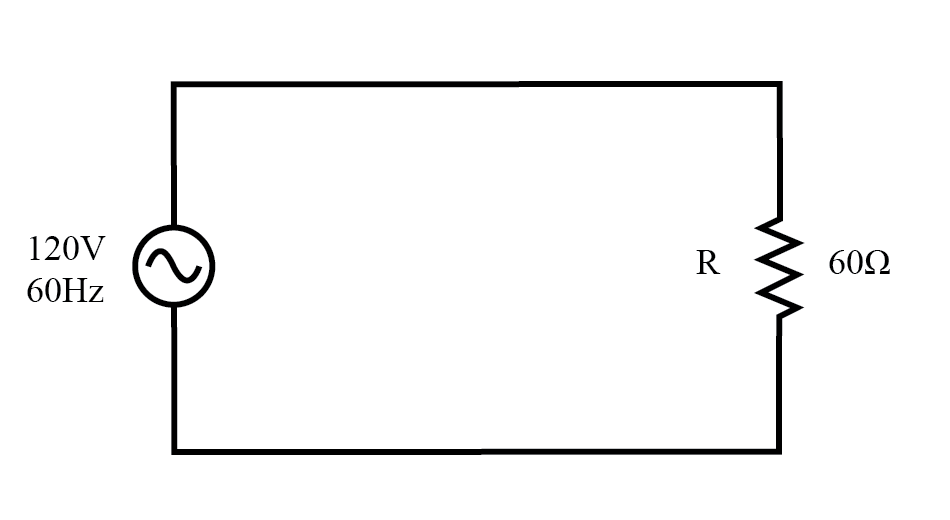
交流电源驱动纯电阻负载。

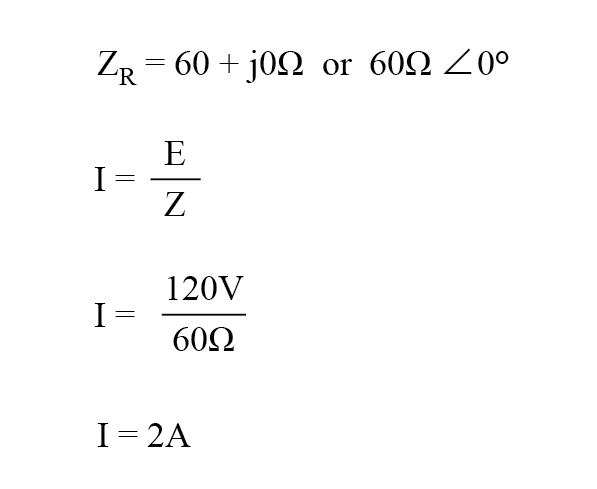
在本例中，负载的电流为 2 安培，RMS。负载消耗的功率为 240 瓦。

由于该负载为纯电阻性（无电抗），因此电流与电压同相，计算类似于等效直流电路中的计算。

如果我们绘制该电路的电压、电流和功率波形，则如下图所示。

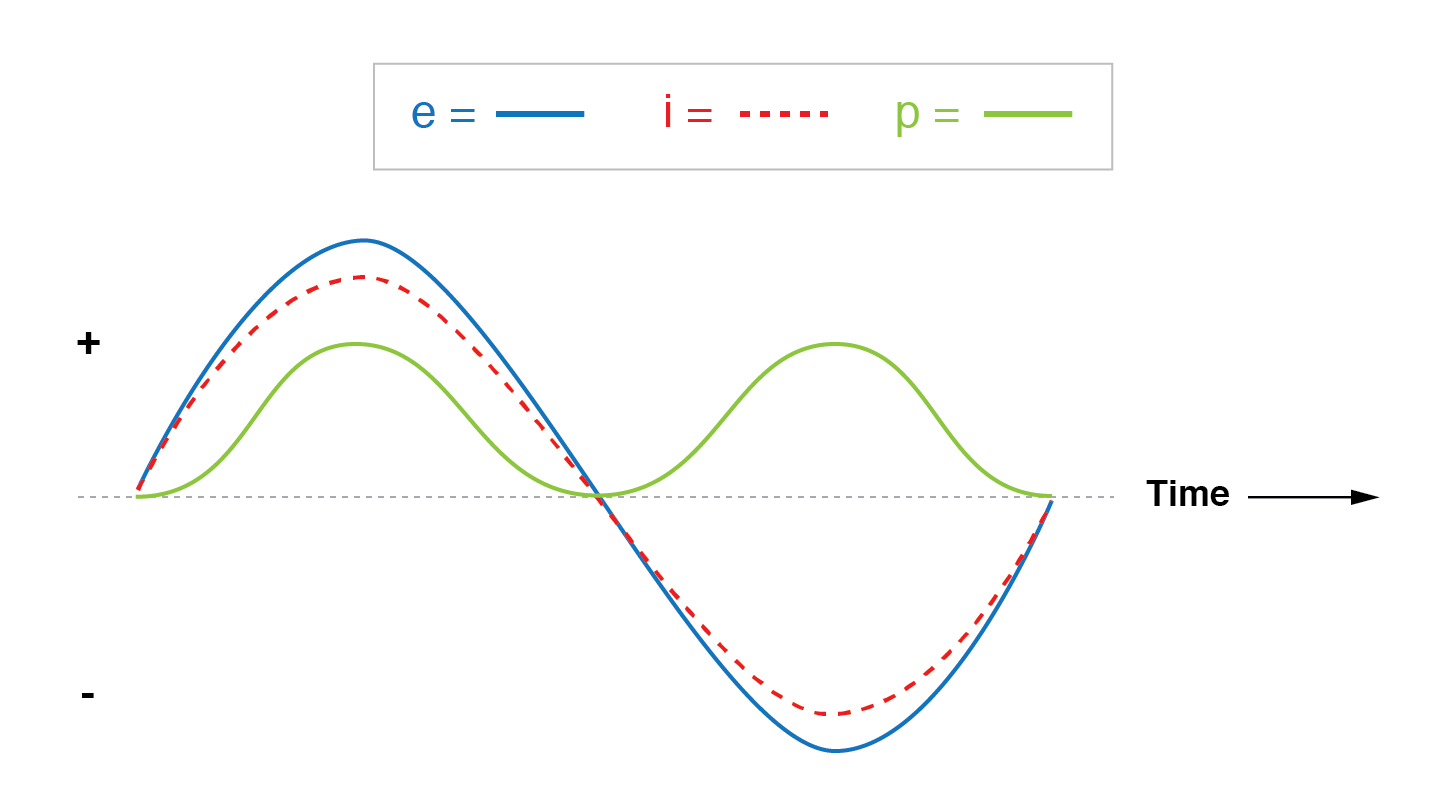
电阻电路中的电流与电压同相。

请注意，该电阻电路的电源波形始终为正，绝不为负。

这意味着功率总是由电阻负载耗散，并且永远不会像使用无功负载那样返回到电源。如果源是机械发电机，转动轴需要 240 瓦的机械能（约 1/3 马力）。

另请注意，功率波形与电压或电流的频率不同！相反，它的频率是两倍 电压或电流波形。

这种不同的频率禁止我们使用与电压、电流和阻抗相同的复杂（矩形或极性）符号表示交流电路中的功率，因为​​这种形式的数学符号意味着不变的相位关系。

当频率不同时，相位关系会不断变化。

尽管看起来很奇怪，但进行交流功率计算的最佳方法是使用标量 符号并用三角法处理任何相关的相位关系。

带有纯无功负载的交流电路

为了比较，让我们考虑下图中带有纯无功负载的简单交流电路。

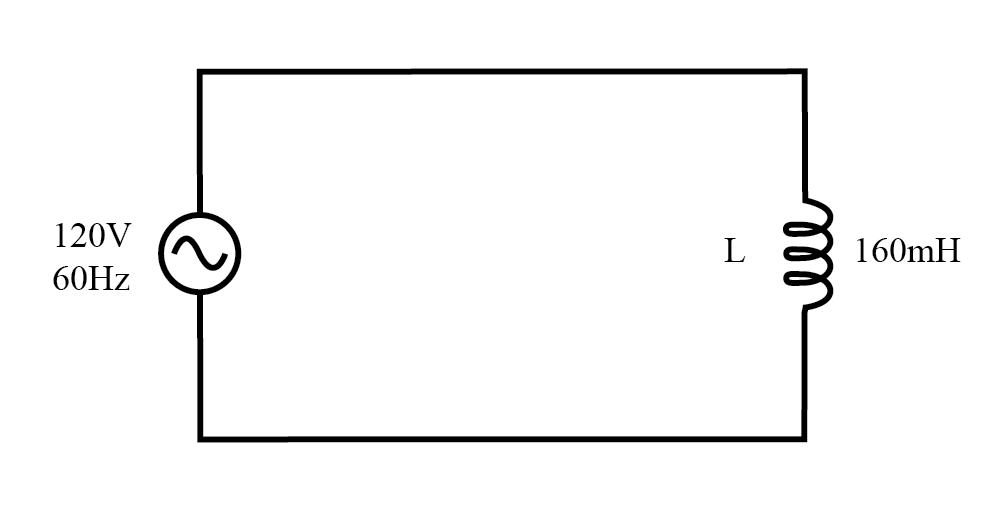
带有纯电抗（感性）负载的交流电路。

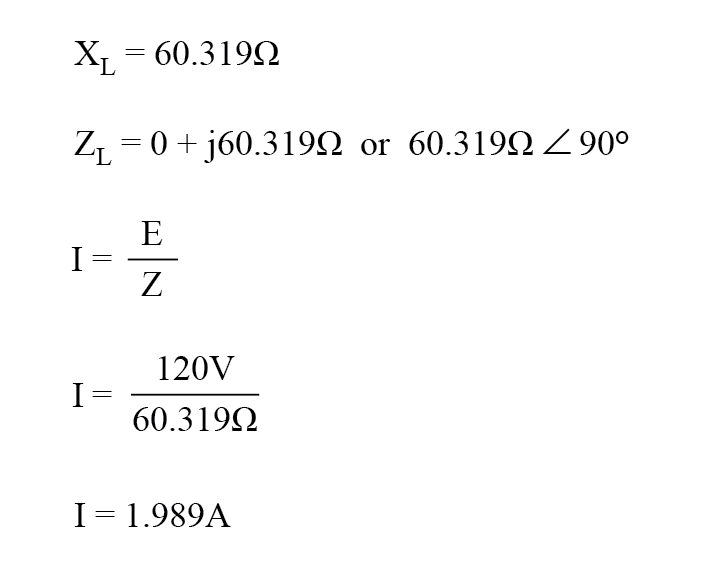
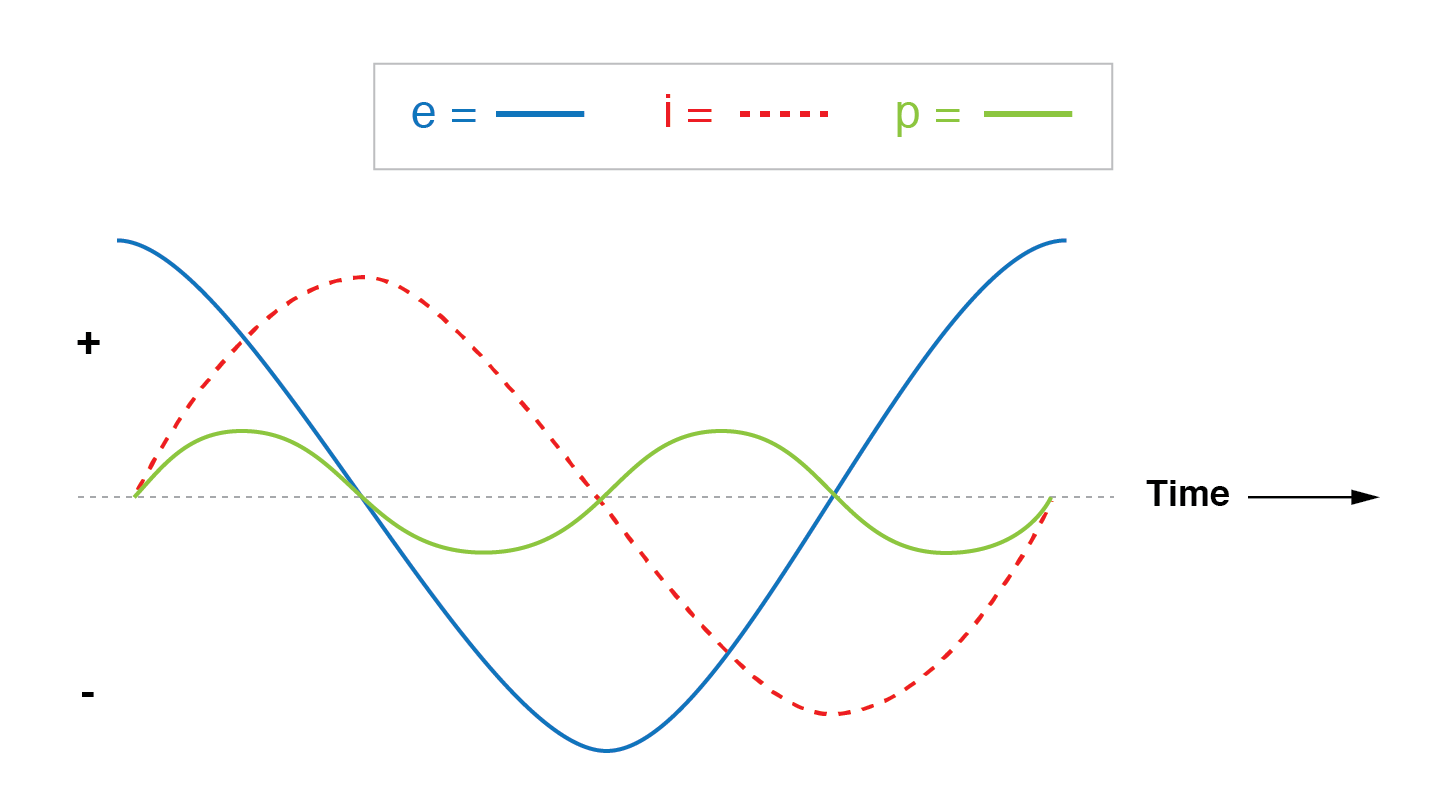
功率不会在纯电抗负载中耗散。虽然它交替地从源头吸收和返回。

请注意，功率在正负循环之间交替交替。 （上图）这意味着能量交替地从源头吸收和返回。

如果源是机械发电机，则（实际上）不需要净机械能来转动轴，因为负载不会使用功率。

发电机轴容易旋转，电感不会像电阻那样发热。

带有阻性和纯无功负载的交流电路

现在，让我们考虑一个负载由下图中的电感和电阻组成的交流电路。

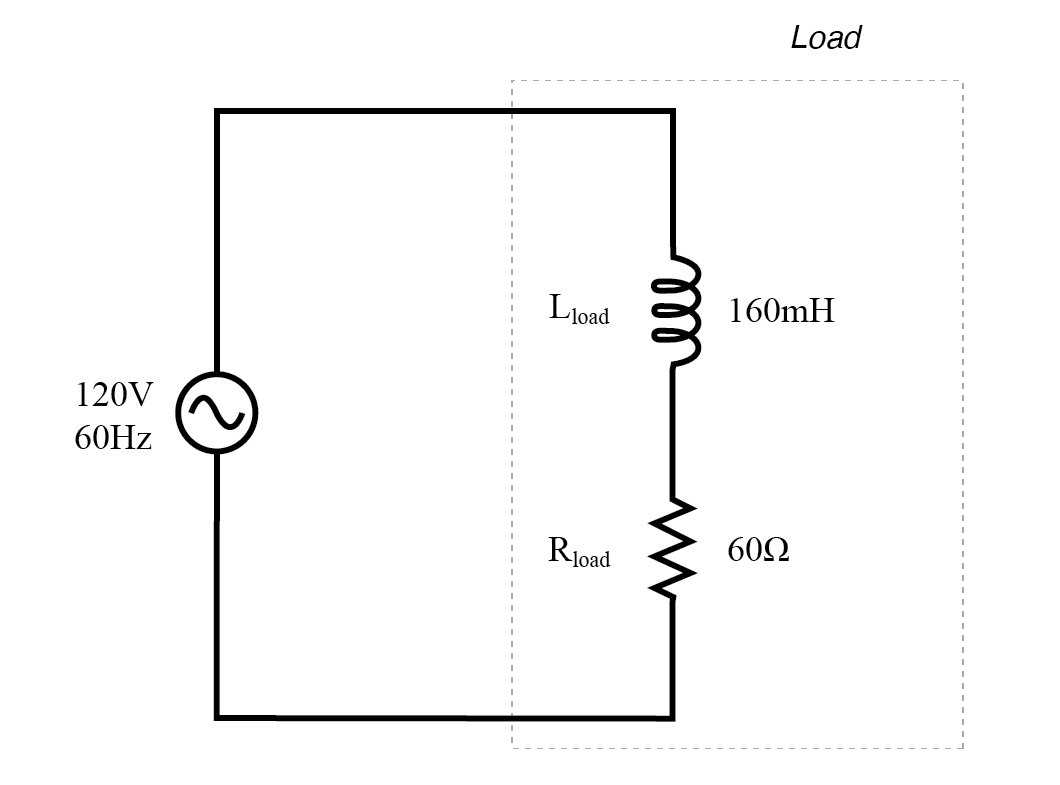
具有电抗和电阻的交流电路。

在 60 Hz 的频率下，160 毫亨的电感给我们 60.319 Ω 的感抗。

该电抗与 60 Ω 电阻结合形成总负载阻抗 60 + j60.319 Ω，或 85.078 Ω ∠ 45.152 ^o .如果我们不关心相角（此时我们不关心），我们可以通过取电压源的极值（120 伏）并将其除以阻抗的极值来计算电路中的电流(85.078 Ω)。

电源电压为 120 伏 RMS，我们的负载电流为 1.410 安培。这是一个有效值电流表在与电阻和电感串联时会显示的数字。

我们已经知道无功元件消耗零功率，因为​​它们同样从电路的其余部分吸收功率并将功率返回到电路的其余部分。

因此，该负载中的任何感抗同样会耗散零功率。

此处唯一需要耗散功率的是负载阻抗的电阻部分。如果我们查看该电路的电压、电流和总功率的波形图，我们会在下图中看到这种组合是如何工作的。

组合电阻/电抗电路消耗的功率多于返回源的功率。电抗不耗散功率；不过，电阻确实可以。

与任何无功电路一样，功率随时间在正负瞬时值之间交替变化。

在纯电抗电路中，正负功率之间的交替被均分，导致净功耗为零。但是，在这种混合电阻和电抗的电路中，电源波形仍然会在正负之间交替，但正电源的数量会超过负电源的数量。

换言之，感性/阻性负载的组合将消耗比返回源更多的功率。

查看功率的波形图，应该很明显，波在中心线的正侧花费的时间比在负侧花费的时间多，这表明负载吸收的功率多于返回到电路的功率。

发生的很少的功率返回是由于电抗造成的；正负功率的不平衡是由于电阻将能量耗散到电路外部（通常以热量的形式）。

如果源是机械发电机，则转动轴所需的机械能量将是正负功率循环之间的平均功率量。

用数学方法表示交流电路中的功率是一项挑战，因为功率波与电压或电流的频率不同。

此外，功率的相位角意味着与电压或电流的相位角完全不同的东西。而电压或电流的角度代表相对时序偏移 在两波之间，功率的相位角代表一个比率 耗散功率和返回功率之间。

由于交流功率不同于交流电压或电流的这种方式，实际上通过使用标量计算得出功率数字更容易 电压、电流、电阻和电抗的数量，而不是试图从 矢量 , 或 复杂 到目前为止我们已经使用过的电压、电流和阻抗的数量。

评论：

• 在纯电阻电路中，所有电路功率都由电阻器耗散。电压和电流同相。
• 在纯电抗电路中，负载不会消耗任何电路功率。相反，功率交替地从交流电源吸收和返回到交流电源。电压和电流的相位相差 90°。
• 在由电阻和电抗混合组成的电路中，负载消耗的功率将大于返回的功率，但肯定会消耗一些功率，而有些仅会被吸收和返回。这种电路中的电压和电流将相差 0° 到 90° 之间的某个值。

相关工作表：

• 交流电源工作表