SUPERMESH 电路分析 |逐步解决示例

Supermesh 分析 – 声明 ，公式，解决的例子

什么是超网格分析？

超网格或超网格分析 是一种比使用网格分析更好的技术分析如此复杂的电路或网络，其中两个网格将电流源作为公共元件。这与我们使用超级节点电路分析的情况相同而不是节点或节点电路分析 为了简化分配超级节点的网络，将电压源完全封闭在超级节点内，并将每个电压源的非参考节点数量减少一 (1) 个。

在supermesh电路分析技术中，电流源在supermesh的内部区域。因此，我们能够将电路中存在的每个电流源的网格数量减少一 (1) 个。

如果电流源（在该网格中）位于电路的周边，则可以忽略单个网格。或者，KVL（基尔霍夫电压定律）仅适用于更新电路中的那些网格或超网格。

顺便说一下Preamble很难理解，所以我们先通过supermesh电路分析解决一个简单的电路，然后总结整个supermesh分析（步骤一步一步）。

相关文章：SUPERNODE 电路分析 |逐步解决示例

解决的超网格分析示例

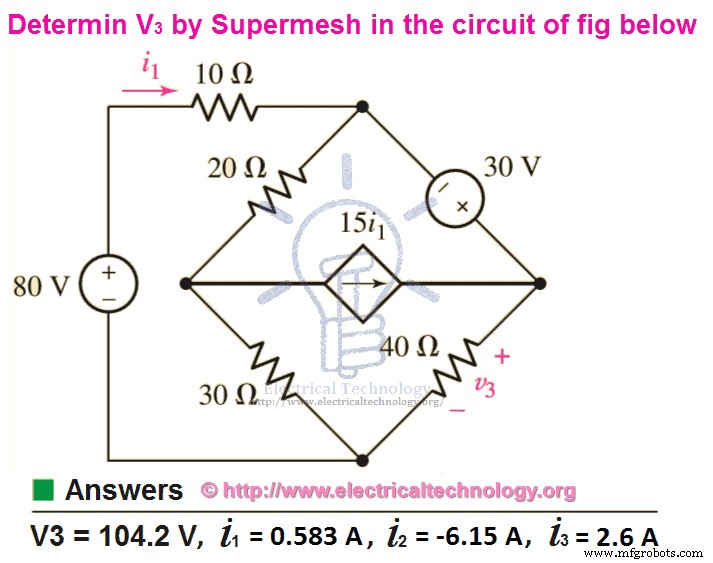
示例：

使用Mesh分析找出V3和Current i 1 , 我 2 和我 3 在下图中？

解决办法：

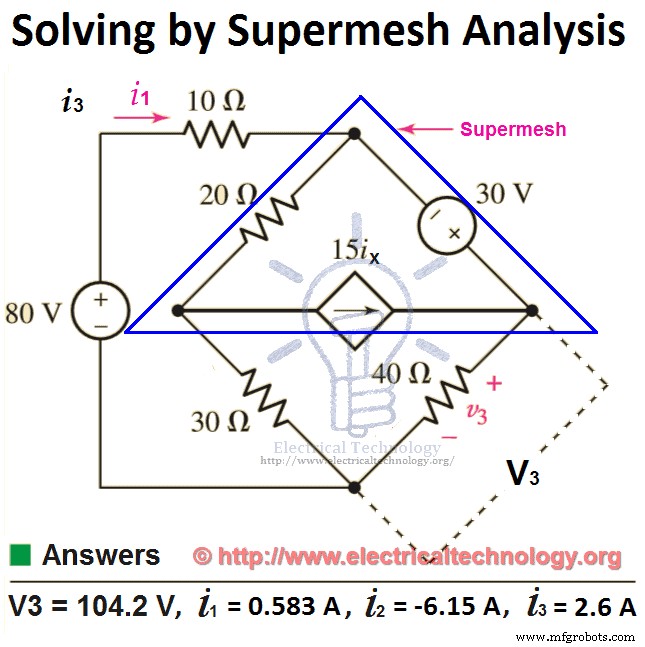
在网格 1 上使用 KVA。

80 =10i 1 + 20(我 1 – 我 2 ) + 30 (我 1 - i3 )

简化

80 =10i 1 + 20我 1 – 20我 2 + 30我 1 - 30我 3

80 =60i 1 – 20我 2 – 30我 3 ….. → 等式 1。

现在申请 KVL 关于超级网格 （这是 mesh 2 的集成和 网格 3 ，但我们已将其减少为单个网格，称为 supermesh )

30 =40i 3 + 30(我 3 - 我 1 ) +20(我 2 - 我 1 )

30 =40i 3 + 30我 3 - 30我 1 + 20我 2 - 20我 1

30 =70i 3 – 50我 1 + 20我 2 ….. → 等式 2。

但是在这里，我们有三 (3) 个变量，即 i 1、我 2和我 3. 有两个方程。所以我们还需要三个方程。

独立的电流源（在supermesh ) 与假定的网格电流有关，即

15i x =我 3 – 我 2

i 3 =15我 x + 我 2 ….. → Eq 3.

通过克莱默法则或求解方程1、2和3 克莱默的 规则计算器 , 消除 , 高斯消除 或计算机辅助程序 如MATLAB ，我们发现

i 1 =0.583 A

i 2 =-6.15 元

i 3 =2.6 A

另外，我们可以找到V3的值 ,

V3 =i 3 x R3

放置值，

V3 =2.6A x 40Ω

V3 =104 V.

Supermesh分析总结（一步一步）

判断电路是否为平面电路 .如果是，请应用 Supermesh。如果否，则改为执行节点分析。
重绘电路 如有必要，计算电路中的网格数。
标记电路中的每个网格电流 .根据经验，将所有网格电流定义为顺时针流动可以简化电路分析。
如果电路包含两个网格的电流源，则形成一个超网格 .因此，超级网格将包含两个网格。
写一个 KVL ( 基尔霍夫的 电路中每个网格和超网格周围的电压定律 .从一个简单的开始，将安装一个节点。现在沿着网格电流的方向进行。在编写KVL方程和求解电路时，在帐户中输入“-”号。如果电流源位于网格的外围，则不需要 KVL 方程。因此，网状电流是通过检查来确定和评估的。
每个定义的超网格都需要一个 KCL（基尔霍夫电流定律），并且可以通过简单应用 KCL 来完成。 简而言之，将每个电流源的电流与网状电流相关联。
如果电路包含更多依赖源，则可能会发生其他情况。 在这种情况下，用合适的网格电流表示任何其他未知值和量，例如电流或电压，而不是网格电流。
排列和组织方程组。
最后，求解节点电压的方程组 比如V1、V2、V3等，都会有Mesh的。如果您发现求解方程组有困难，请参考上面的示例。