克莱默法则计算器 - 2 和 3 方程系统

用于线性电路分析的克莱默规则和计算器 |逐步解决的例子

今天，我们将分享另一种简单但功能强大的电路分析技术，称为“克莱默法则 “.

SUPERMESH 电路分析 |逐步解决示例

更新： 我们添加了在线克莱默规则计算器，您可以在其中求解两个方程组和三个方程组。检查帖子的两个部分中的两个克莱默规则计算器。谢谢

以下是求解示例的分步教程，详细说明了如何使用克莱默规则求解复杂的电路和网络。

2×2 的克莱默规则计算器（二方程系统）

示例 2： 使用网格分析来确定下面电路中的三个网格电流。使用 Cramer 规则进行简化。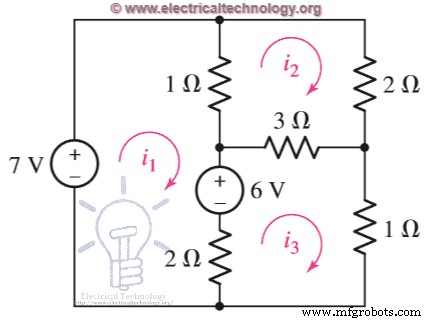

首先，在每个网格上一个一个地应用KVL，并写出它的方程。 -7+1(我 1–我 2) +6+2(我 1–我 3) =0 1(i 2– 我 1) + 2我 2 + 3(我 2– 我 3) =0 2(我 3– 我 1) – 6+3(我 3– 我 2) + 1我 3 =0 简化， 3i 1 - 我 2 - 2我 3 =1 … 等式….. (1) – i 1 + 6我 2 - 3我 3 =0 … 等式….. (2) -2i 1 - 3我 2 + 6我 3 =6 ... Eq.. (3) 现在，将上述方程写成矩阵形式。 3我 1– 我 2– 2我 3 =1 –我 1+ 6我 2– 3我 3 =0-2我 1-3我 2+ 6我 3 =6

现在，我们将找到Δ的系数行列式。我们将如何做到这一点？只需检查下图以获得更好的解释。点击图片放大

所以完整的步骤如下所示。

Δ =+3 (6 x 6) – (- 3 x –3) – (-1 (- 1 x 6)-(-2 x –3) + (-2 (-1 x –3) – (-2 x 6)Δ =81 -12 -30 =39 现在，通过与上述相同的方式找到 Δ1。但是，只需将矩阵的第一列替换为“答案列”即可。有关详细信息，请查看下图。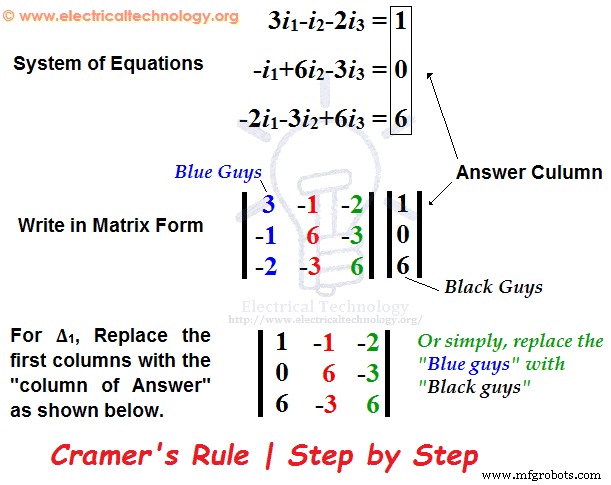

所以，这里是找到Δ1的完整步骤。在这里，我们将第一列中的“Blue Guys”替换为“Black Guys”:)。

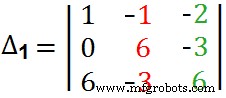=+1(36-9) – (–1[0+18]) –2(0- 36)=27 + 18 + 72Δ1 =117 再次用前面解释的方法求出 Δ2。只需将矩阵的第二列替换为“答案列”，即将中心列中的“红人”替换为“黑人”，如下所示。

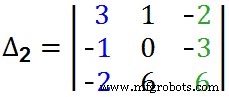=+3 (0 +18) -1[(-6)-(+6)] –2 (-6-0)=54+12+12 =78Δ2 =78 最后，找到最后一个 Δ3。只需将第三列替换为“答案列”，即将第三列中的“绿人”替换为“黑人”，如下所示。

=+3 (6 x 6) – (-3 x 0) – [-1(-1 x 6) – (-2 x 0)] + [1(-1) x (-3) – (-2) x (6)]=108 + 6 + 15Δ3 =117 现在，求解并找出未知值当前的，即 i 1、我 2和我 3.正如克莱默法则所说，变量即i 1 =Δ1/Δ1，我 2 =Δ/Δ2 和我 3 =Δ/Δ3。 因此，我 1 =Δ1/Δ1 =117/39我 1 =3A 还有我 2 ,我 2 ==Δ/Δ2 =78/39我 2 =2A 最后，我 3;我 3 =Δ/Δ3 =117/39我 3 =3A。我希望您非常了解 cramer 的规则，并享受分步教程。请不要忘记与您的朋友分享。此外，在下面的框中输入您的电子邮件地址以订阅。因此，我们将向您发送更多类似上述的教程。谢谢。