什么是网络分析？

一般来说，网络分析 是用于对电路（互连组件的“网络”）进行数学分析的任何结构化技术。技术人员或工程师经常会遇到包含多个电源或组件配置的电路，这些电路无法通过串联/并联分析技术进行简化。在这些情况下，他或她将被迫使用其他方式。本章介绍了一些有助于分析此类复杂电路的技术。

分析一个简单的电路

为了说明即使是简单的电路也无法通过分解为串联和并联部分来进行分析，请从这个串并联电路开始：

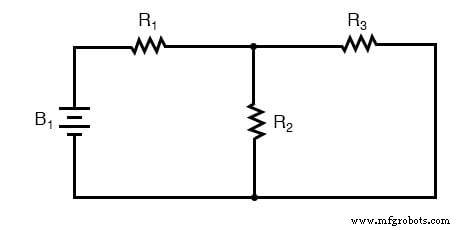
要分析上述电路，首先要找出等效于 R2 和 R3 的并联，然后将 R1 串联以得出总电阻。然后，将电池 B1 的电压与该总电路电阻相结合，可以通过使用欧姆定律（I =E / R）计算总电流，然后该电流数字用于计算电路中的电压降。总而言之，一个相当简单的过程。

电路无视串联/并联分析

两个电池电路

然而，再增加一块电池就可以改变这一切：

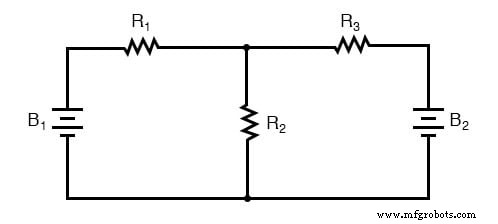
电阻器 R2 和 R3 不再相互并联，因为 B2 已插入到 R3 的电路分支中。仔细检查后，似乎没有 该电路中的两个电阻直接串联或并联。这是主要问题：在串并联分析中，我们首先确定了是的电阻器组 直接串联或并联，将它们减少到单个等效电阻。如果彼此之间没有简单的串联或并联配置的电阻器，那我们该怎么办？

应该清楚的是，这个看似简单的电路，只有三个电阻器，不可能将其简化为简单串联和简单并联部分的组合：它是完全不同的东西。然而，这并不是唯一一种无视串联/并联分析的电路：

不平衡桥电路

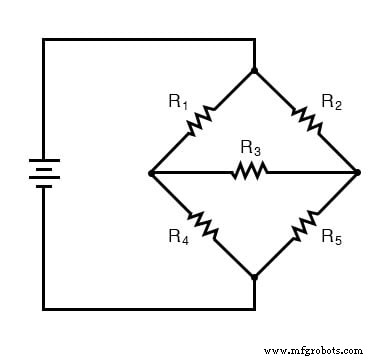
这里我们有一个桥接电路，为了举例，我们假设它不是 平衡（比率 R1/R4 不等于比率 R2/R5）。如果是平衡的，则通过R3的电流为零，可以将其视为串联/并联组合电路（R1-R4 // R2-R5）。但是，通过 R3 的任何电流都无法进行串联/并联分析。 R1 不与 R4 串联，因为电流还有另一条路径，即通过 R3。出于同样的原因，R2 也不与 R5 串联。同样，R1 不与 R2 并联，因为 R3 将其底部引线分开。 R4 也不与 R5 并联。啊啊啊啊啊！

尽管此时可能并不明显，但主要问题是存在多个未知量。至少在串联/并联组合电路中，有一种方法可以找到总电阻和总电压，将总电流作为单个未知值进行计算（然后该电流用于满足还原过程中先前未知的变量，直到可以分析整个电路）。对于这些问题，在电路简化的最基本层面上，有不止一个参数（变量）是未知的。

对于两节电池电路，无法得出“总电阻”的值，因为有两个 提供电压和电流的电源（我们需要两个 “总”电阻，以便进行任何欧姆定律计算）。对于不平衡的桥式电路，有一个电池总电阻这样的事情（为计算总电流铺平了道路），但总电流立即在桥的每一端分成未知的比例，所以没有进一步可以进行电压的欧姆定律计算（E=IR）。

那么当我们面临电路中的多个未知数时，我们该怎么办？答案最初是在称为联立方程的数学过程中找到的 或方程组 ，从而通过在多个方程中将多个未知变量相互关联来求解多个未知变量。在只有一个未知数的情况下（例如我们迄今为止处理的每个欧姆定律方程），只需要一个方程来求解单个未知数：

然而，当我们求解多个未知值时，我们需要有与未知数相同数量的方程才能得到解。有几种求解联立方程的方法，对于本章的解释来说，这些方法都非常复杂且令人生畏。然而，许多科学和可编程的计算器都能够解决同时出现的未知数，因此建议在第一次学习如何分析这些电路时使用这样的计算器。

这并不像乍看起来那么可怕 .相信我！

稍后，我们会看到一些聪明的人找到了避免在这些类型的电路上使用联立方程的技巧。我们称这些技巧为网络定理 ，我们将在本章稍后部分进行探讨。

评论：

• 由于存在多个未知值，某些电路配置（“网络”）无法根据串联/并联电路规则通过减少来解决。
• 求解多个未知数的数学技术（称为“联立方程”或“系统”）可以应用于基本电路定律来求解网络。

相关工作表：

• 直流支路电流分析工作表
• 串并联直流电路工作表