替换定理 - 带求解示例的分步指南
用替代定理分析和解决电路
替代定理
顾名思义,替代定理是用来将电路的一个元素替换为另一个元素。但在更换元件时,必须牢记电路的行为不应该改变。
替换定理表明;
这个定理用来证明几个定理。为了替换网络的一个分支,这个定理告诉我们边界条件。
如果电流值通过支路并且支路两端的电压值已知,我们可以用电压源、电流源等其他元件替换这个支路,不同的电阻值等,通过这样做,初始条件保持不变。
当电路有两个以上串联或并联的源时,此定理不适用。
- 相关文章:戴维南定理。带有已解决示例的分步指南
代入定理解释
替换定理是用具有不同元素的等效分支替换网络的任何分支。在这个定理中,如果任何一个支路或元件被一个与原网络相同的电压和电流源所代替,则具有该支路的电压和电流。
让我们用下图所示的网络来理解替换定理。
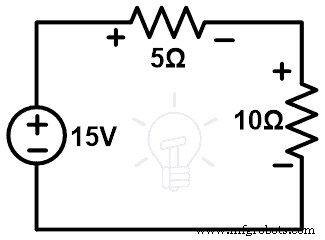
如上图所示,它有两个电阻串联一个直流电源。现在,我们将尝试用其他元素替换任何分支或元素。在此之前,我们需要知道通过所有分支的电压和电流。
这里,这个电路只有一个循环。因此,通过所有分支和元件的电流是相同的。这个电流可以通过将KVL应用于网络来确定。
比如说,我通过环路的电流量。
+15 =5我 + 10我
15 =15我
我 =1A
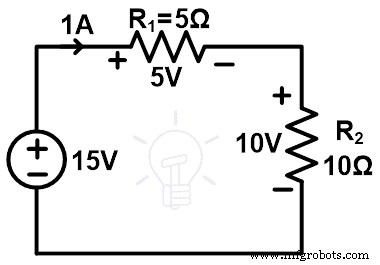
所以,通过每个元素的电流为1A。现在,我们需要找到所有元素的电压。
一个分支有电压源。所以,我们没有找到那个分支的电压。该电压分为两个电阻。我们需要找到每个电阻上的电压。可以通过应用分压器规则找到。
所以,5Ω电阻两端的电压为;
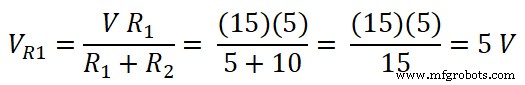
同理,10Ω电阻两端的电压为;
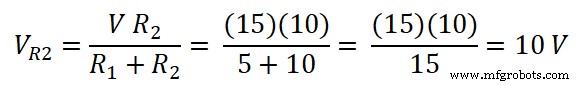
- 相关文章:诺顿定理。带有已解决示例的分步指南
Substitute-1
我们可以将10Ω电阻支路换成10V电压源,如下图所示。
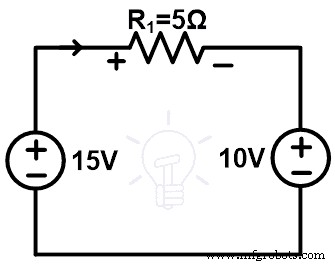
现在,将KVL应用于网络,
+15 – 10 =5我
5 =5我
我 =1一个
所以,回路电流与原电路相同。现在,计算元件之间的电压。 10Ω 电阻支路被 10V 电源取代。因此,该分支上的电压为 10V。而且这个电压和原电路中那个支路的电压是一样的。
现在,找到 5Ω 电阻支路的电压。通过该支路的电流为1A。因此,根据欧姆定律;
V 5Ω =1A × 5 =5V
所以,电流通过所有支路,所有支路电压与原网络相同。
Substitute-2
去掉5Ω电阻支路。并用 5V 电压源替换这个分支。本次代换的电路图如下图所示。
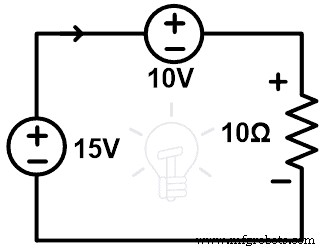
现在,计算所有分支的电流和电压,并与原始网络进行比较。
要找到通过循环的电流,应用KVL;
+15 – 5 =10I
10 =10I
我 =1一个
因此回路电流或通过元素的电流与通过原网络的电流相同。
将5Ω电阻支路换成5V电压源。因此,该支路的电压与原始网络中的电压相同。现在,我们需要计算 10Ω 电阻支路的电压。
通过10Ω电阻支路的电流为1A。根据欧姆定律;
V 10Ω =红外
V 10Ω =1 × 10
V 10Ω =+10 V
所以,将5Ω电阻换成5V电压源后,网络的行为并没有改变。
- 相关文章:叠加定理 - 带求解示例的电路分析
Substitute-3
去掉10Ω电阻支路,换成1A电流源。替换后的电路图如下图所示。
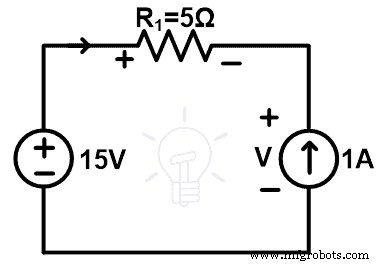
电路中有电流源。因此,通过回路的电流与电流源的量相同。在这种情况下,1A 电流源连接到网络。因此,通过环路的电流为1A,与通过原始网络的电流相同。
现在,计算 5Ω 电阻和 1A 电流源两端的电压。
根据欧姆定律,
V 5Ω =红外
V 5Ω =1 × 5
V 5Ω =+5 V
现在,求 1A 电流源的电压。假设 1A 电流源两端的电压为 V。
从上图看;
+15 – 5 – V =0
V =+10 V
所以,用1A电流源代替10Ω电阻后,证明所有元件上的电压和流过所有元件的电流与原网络相同。
- 相关文章:米尔曼定理 - 分析交流和直流电路 - 示例
Substitution-4
移除 10Ω 电阻支路,并用与 5V 电压源串联的 5Ω 电阻代替。该替代品的电路图如下图所示。
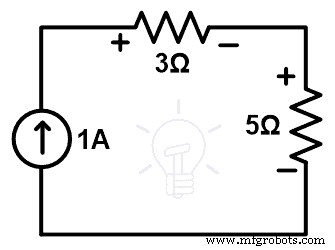
现在,我们需要找到当前通过循环。因此,将 KVL 应用到上述网络中。
15 – 5 =5I + 5我
10 =10I
我 =1A
所以,当前通过的元素和原来的网络是一样的。现在,找出所有元件上的电压。
求5Ω电阻两端的电压;我们使用欧姆定律。
V 5Ω =红外
V 5Ω =1 × 5
V 5Ω =5 V
现在,我们找到了 A 点和 B 点之间的电压。
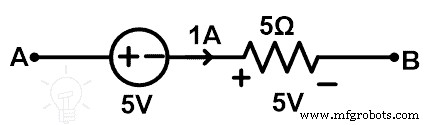
由上图可知,通过5Ω电阻的电流为1A。因此,该元件两端的电压为 5V。 A点和B点之间的总电压为
V AB =5 + V 5Ω
V AB =5 + 5
V AB =+10V
因此,在用 5Ω 电阻和 5V 电压源替换 10Ω 电阻支路后,网络的行为保持不变。
因此,我们可以说有几种方法可用于在不改变元素的电压和电流且不改变网络行为的情况下找到任何网络元素的替代物网络。
- 相关文章:Tellegen 定理 - 求解示例和 MATLAB 仿真
使用替代定理求解网络的步骤
步骤一 找出网络中所有元素的电压和电流。一般通过简单的KCL、KVL或欧姆定律就可以计算出电压和电流。
第二步 找到相关分支,您希望通过不同的元素(如电流源、电压源或电阻)移除。
第三步 在电压和电流不发生变化的情况下,找到合适的替代元素值。
第四步 通过计算所有元件的电压和电流来验证新电路。并将其与原始网络进行比较。
这都是关于替换定理的。现在,让我们举个例子。
- 相关文章: 交流和直流电路的最大功率传输定理
替代定理的例子及解
使用代换定理求解下面的网络,计算所有电阻器中的电流和电压。
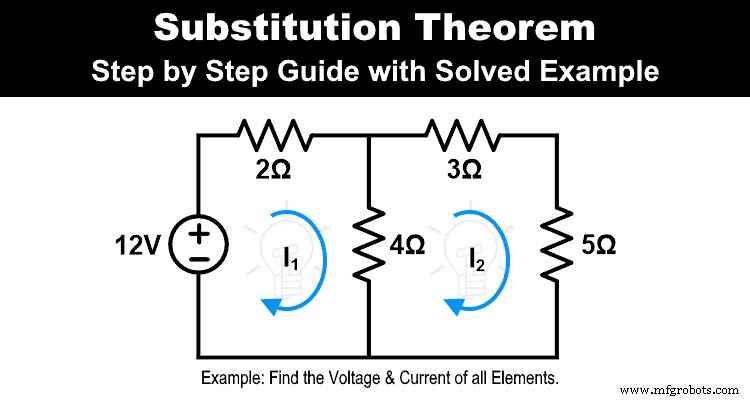
步骤一 求所有元素的电压和电流。为此,在本例中,我们将 KVL 应用于网络。
在loop-1应用KVL;
14 =6我 1 - 4我 2 … (1)
在loop-2应用KVL;
0 =12我 2 - 4我 1
12我 2 =4我 1
我 1 =3我 2 … (2)
将此值代入方程-1;
14 =6(3I 2) – 4我 2
14 =18我 2 – 4我 2
14 =14我 2
我 2 =1A
来自方程-2;
我 1 =3A
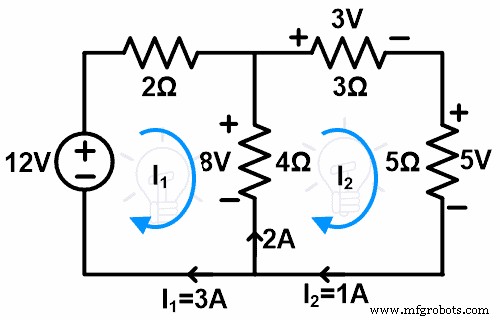
第二步 现在,我们将删除 loop-1 的分支,并创建一个循环。
第三步 我们可以用电压源或电流源代替4Ω电阻。在这里,我们将放置一个电流源。
通过loop-2的电流为1A。因此,我们将支路替换为 1A 电流源。所以剩下的电路如下图所示。

第四步 让我们验证所有元素的电压和电流。
这个网络只有一个循环。这个回路有一个电流源。因此,通过回路的电流值与电流源的值相同。
这里,当前源的值为1A。因此,通过3Ω和5Ω电阻支路的电流为1A,与原网络相同。
现在,使用欧姆定律求 3Ω 电阻两端的电压;
V 3Ω =红外
V 3Ω =1 x 3
V 3Ω =3V
现在,使用欧姆定律求 5Ω 电阻两端的电压;
V 5Ω =红外
V 5Ω =1 x 5
V 5Ω = 5V
所以电压和电流跟原来的网络是一样的。这就是替代定理的工作原理。
如果我们在步骤 3 中选择电压源,而不是电流源。在这种情况下,电压源的值与4Ω电阻支路的值相近。
原网络中,通过4Ω电阻支路的电流为;
我 1 - 我 2 =3 – 1 =2A
根据欧姆定律;
V 4Ω =2 x 4 =8V
所以,我们需要将8V电压源接入网络,剩下的电路如下图所示。
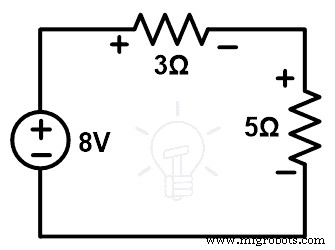
Step-4 验证电压和电流。将 KVL 应用到上述循环中。
8 =3我 + 5我
8 =8我
我 =8A
3Ω电阻两端的电压;
V 3Ω =1 × 3 =3V
5Ω电阻两端的电压;
V 5Ω =1 × 5 =5V
所以,替换后的电压和电流和原来的网络是一样的。
相关电路分析教程:
- SUPERNODE 电路分析 - 逐步解决示例
- SUPERMESH 电路分析 - 逐步解决示例
- 基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
- 克莱默规则计算器 - 电路的 2 和 3 方程系统
- 惠斯通电桥——电路、工作、推导和应用
- 电气和电子工程计算器
- 5000 多个电气和电子工程公式和方程式
工业技术


