求解联立方程：代入法和加法法

什么是联立方程和方程组？

项联立方程 和方程组 指两个或多个未知变量通过相等数量的方程相互关联的条件。

示例：

对于这组方程，x 只有一个值组合 和 y 这将满足两者。

任何一个方程，单独考虑，都具有无限的有效 (x,y) 解决方案，但一起 只有一个。绘制在图表上，这种情况变得明显：

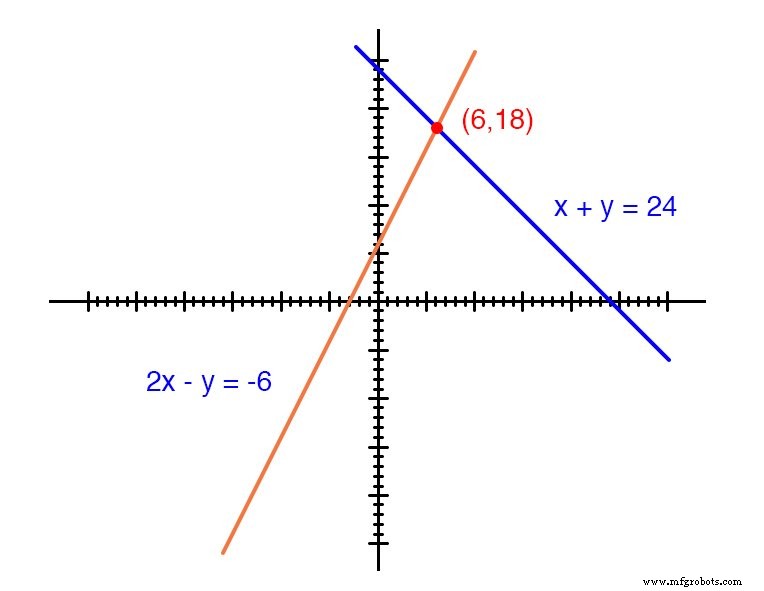
每条线实际上是一个连续的点，代表可能的 x 和 y 每个方程的解对。

每个方程分别有无数个有序对 (x ,y ) 解决方案。两个线性函数只有一点x + y =24 和 2x - y =-6 相交（其中许多独立解中的一个恰好适用于两个方程），这就是 x 等于 6 和 y 的值 等于 18 的值。

但是，通常情况下，绘图并不是确定两个或多个方程的联立解集的非常有效的方法。对于三个或更多变量的系统尤其不切实际。

例如，在三变量系统中，将通过三个平面在三维坐标空间中的点相交来找到解决方案——这不是一个容易可视化的场景。

用代换法求解联立方程

存在几种求解联立方程的代数技术。

也许最容易理解的是替换 方法。

以我们的二变量示例问题为例：

在替代方法中，我们操纵其中一个方程，以便根据另一个变量定义一个变量：

然后，我们采用这个新的定义 一个变量和替换 对于另一个方程中的相同变量。

在这种情况下，我们采用 y 的定义 , 即 24 - x 并将其替换为 y 在另一个方程中找到的项：

现在我们有了一个只有一个变量 (x )，我们可以使用“正常”代数技术来解决它：

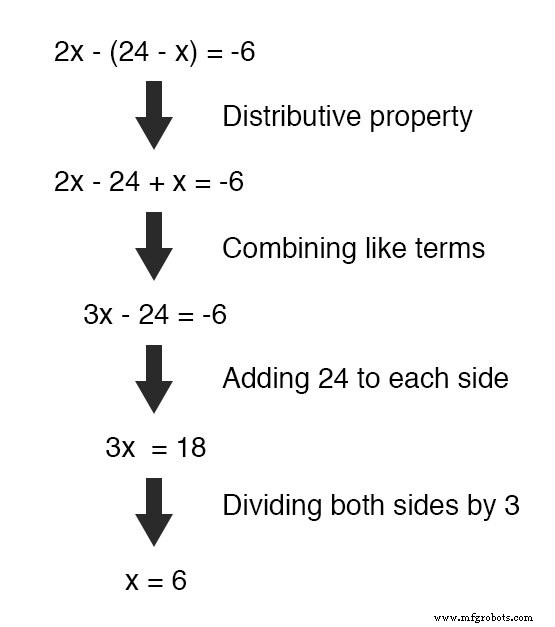
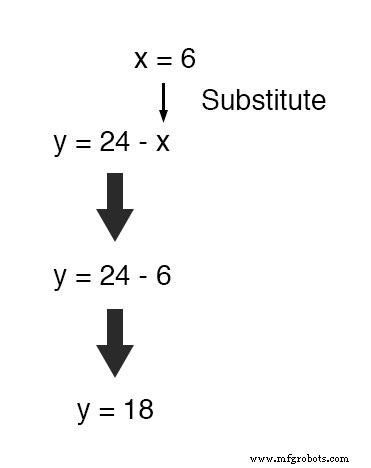
现在 x 已知，我们可以将此值代入任何原始方程中，并获得y的值。

或者，为了节省我们一些工作，我们可以将这个值 (6) 代入我们刚刚生成的方程来定义 y 在 x 方面 ，因为它已经可以求解 y :

将替代方法应用于三个或更多变量的系统涉及类似的模式，只是涉及更多的工作。

对于任何求解方法来说，这通常都是正确的：随着系统中每增加一个变量，获得解所需的步骤数会迅速增加。

要求解三个未知变量，我们至少需要三个方程。考虑这个例子：

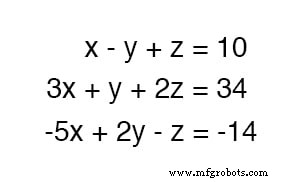
由于第一个方程具有最简单的系数（1、-1 和 1，对于 x , y , 和 z ，分别），使用它来根据其他两个变量来开发一个变量的定义似乎是合乎逻辑的。

求解 x 在 y 方面 和 z :

现在，我们可以替换 x 的这个定义 其中 x 出现在其他两个方程中：

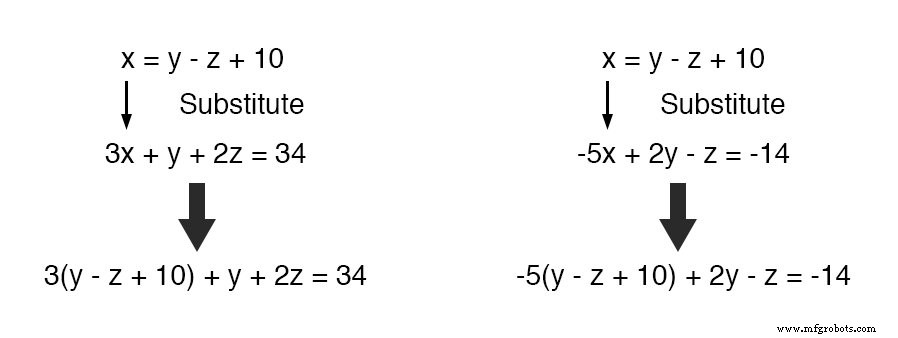
将这两个方程简化为最简单的形式：

到目前为止，我们的努力已经将系统从三个方程中的三个变量简化为两个方程中的两个变量。

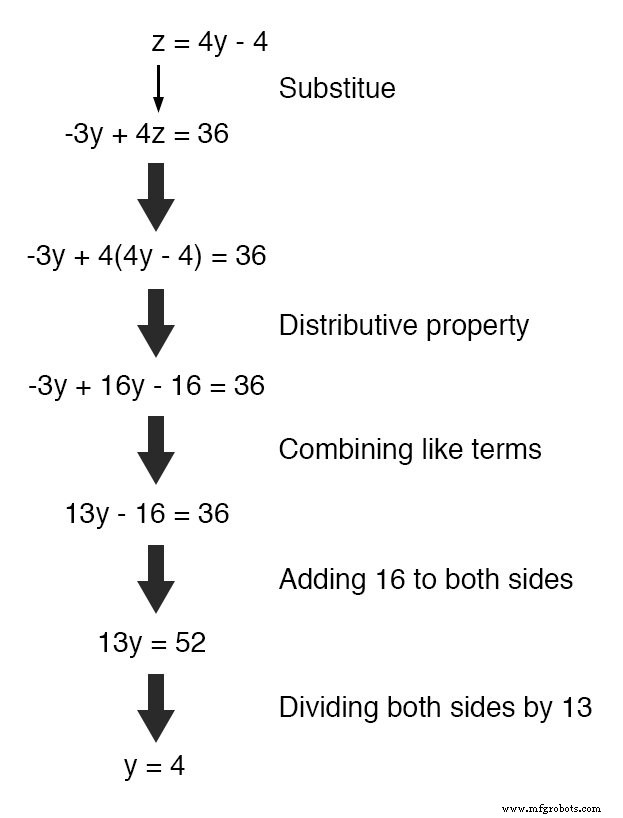
现在，我们可以再次将替换技术应用于两个方程 4y - z =4 和 -3y + 4z =36 解决任一 y 或 z .首先，我将操纵第一个方程来定义 z 在 y 方面 ：

接下来，我们将替换 z 的这个定义 在 y 方面 我们看到的地方 z 在另一个等式中：

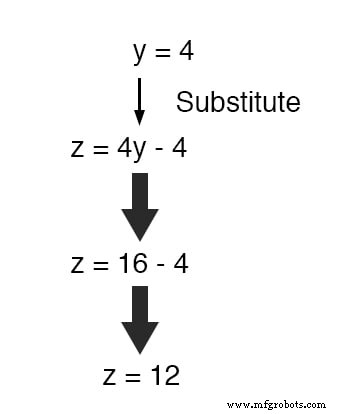
现在y 是一个已知值，我们可以将其代入定义 z 的方程中 在 y 方面 并获得 z 的数字 ：

现在，使用 y 的值 和 z 已知，我们可以将它们代入我们定义 x 的等式中 在 y 方面 和 z , 获取 x 的值 ：

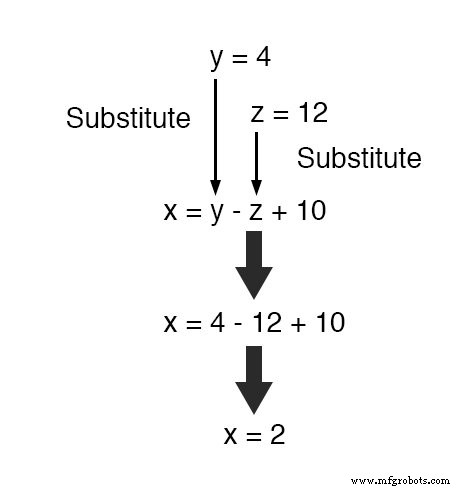
最后，我们找到了 x 的值 , y , 和 z 分别满足三个方程的 2、4 和 12 个。

用加法求解联立方程

虽然在概念层面上替代方法可能最容易掌握，但我们也可以使用其他解决方法。

其中一种方法是所谓的加法 方法，即为消除变量项的目的，将方程相互相加。

让我们以我们用来演示替代方法的二变量系统为例：

最常用的代数规则之一是，您可以对等式执行任何您希望的算术运算，只要您对两边均等 .

关于加法，这意味着我们可以在等式两边加上我们想要的任何数量——只要它相同 数量——不改变等式的真实性。

那么，我们有一个选择，就是将方程的对应边相加，形成一个新方程。

由于每个方程都是等式的表达式（= 两边的相同量 符号），将一个方程的左边添加到另一个方程的左边是有效的，只要我们将两个方程的右边也加在一起即可。

例如，在我们的示例方程组中，我们可以添加 x + y 到 2x - y , 并添加 24 和 -6 一起形成一个新的方程。

这对我们有什么好处？检查当我们对示例方程组执行此操作时会发生什么：

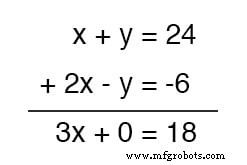
因为上面的方程恰好包含一个正的 y 项而底部方程恰好包含负 y 项，这两个项在加法过程中相互抵消，不留y 总和中的术语。

我们剩下的是一个新方程，但只有一个未知变量，x ！这使我们可以轻松求解 x 的值 :

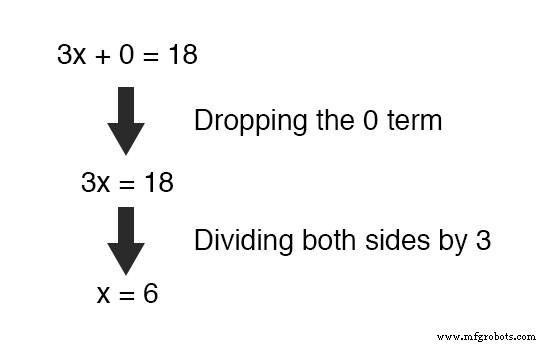
一旦我们知道 x 的值 ，当然，确定 y 的值只是一个简单的替换问题（替换 x 与数字 6 ) 转化为原始方程之一。

在这个例子中，将方程相加的技术可以很好地产生具有单个未知变量的方程。

举个事情不那么简单的例子呢？考虑以下方程组：

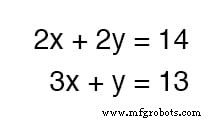
我们可以将这两个方程加在一起——这是一个完全有效的代数运算——但它不会让我们在获得 x 值的目标中受益 和 y :

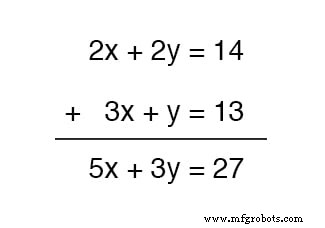
结果方程仍然包含两个未知变量，就像原始方程一样，因此我们无法进一步求解。

但是，如果我们可以操纵其中一个方程以获得一个负项，将 添加时取消另一个方程中的相应项？

然后，系统将简化为具有单个未知变量的单个方程，就像最后一个（偶然的）示例一样。

如果我们只能转动 y 将下等式中的项转化为 - 2y 项，所以当两个方程加在一起时，都 y 方程中的项会抵消，只剩下一个 x 术语，这将使我们更接近解决方案。

幸运的是，这并不难做到。如果我们乘以 下等式的每一项由 -2 ，它将产生我们寻求的结果：

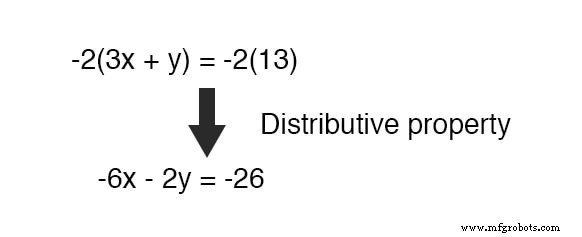
现在，我们可以将这个新方程添加到原来的上方程中：

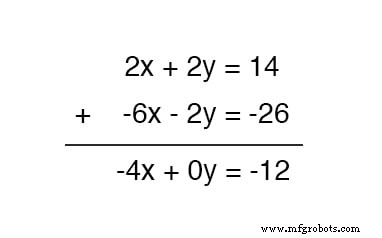
求解 x ，我们得到3的值 :

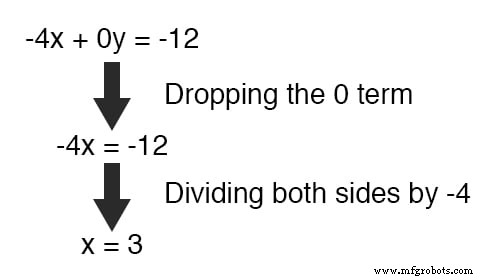
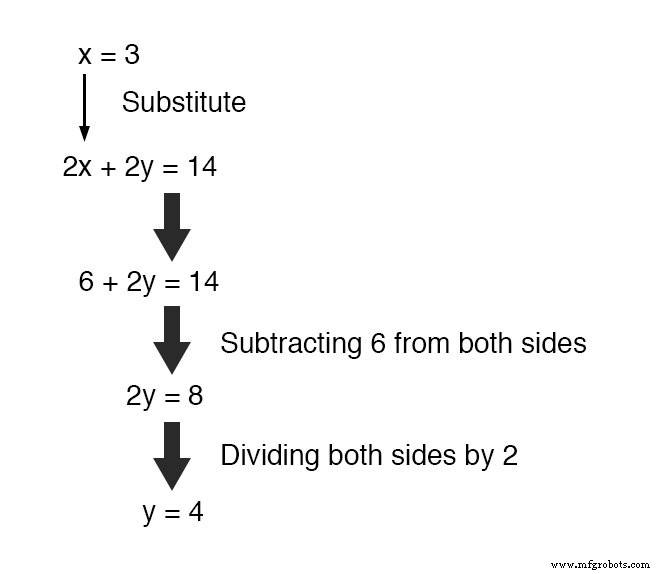
用这个新发现的值替换 x 转化为原始方程之一，y 的值 很容易确定：

在三变量系统上使用这种求解技术要复杂一些。

和代换一样，你必须用这个技巧把三变量的三方程系统化简为两个变量的两个方程，然后再应用它得到一个未知变量的方程。

为了演示，我将使用替换部分中的三变量方程组：

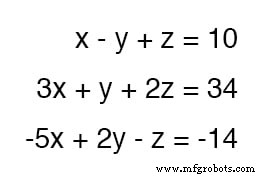
由于顶部方程的系数值为 1 对于每个变量，这将是一个易于操作和用作取消工具的方程。

例如，如果我们想取消 3x 中间方程的项，我们需要做的就是取上面的方程，将它的每一项乘以-3 ，然后将其添加到中间方程中，如下所示：

我们可以去掉它的-5x的底部方程 项以同样的方式：取原始的顶部方程，将其每一项乘以 5 ，然后将修改后的方程添加到底部方程，留下一个只有 y 的新方程 和 z 条款：

此时，我们有两个方程具有相同的两个未知变量，y 和 z :

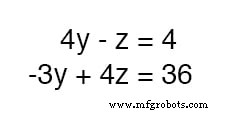
通过检查，应该很明显 -z 可以利用上面方程的项来抵消 4z 下等式中的项，只要我们将上等式的每一项乘以4 并将两个方程相加：

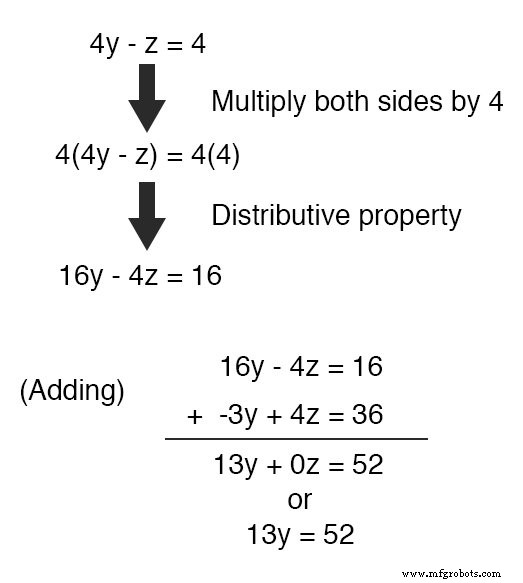
取新方程13y =52 并求解 y （两边除以13 )，我们得到4的值 对于 y .

代入4的这个值 对于 y 在两个变量方程中的任何一个中，我们都可以求解 z .

替换 y 的两个值 和 z 转化为原始的三变量方程中的任何一个都允许我们求解 x .

最终的结果（我将省略代数步骤，因为你现在应该已经熟悉它们了！）是 x =2 , y =4 , 并且 z =12 .

相关工作表：

• 电路分析工作表的联立方程