十进制数转换

由于八进制和十六进制计数系统的基数是二进制的倍数（基数为 2），因此在十六进制或八进制与二进制之间来回转换非常容易。

另外，由于我们对十进制系统非常熟悉，因此将二进制、八进制或十六进制转换为十进制形式相对容易（只需将密码值和位重的乘积相加即可）。

然而，从十进制转换为这些“奇怪”的数字系统中的任何一个都是另一回事。

试错法

可能最有意义的方法是“试一试”方法，您可以尝试将二进制、八进制或十六进制表示法“拟合”为以十进制形式表示的所需值。

例如，假设我想以二进制形式表示 87 的十进制值。让我们从绘制一个二进制数字段开始，并加上位置权重值：

好吧，我们知道在 128 的位置上不会有“1”位，因为这会立即给我们一个大于 87 的值。

然而，由于右边的下一个权重（64）小于 87，我们知道那里一定有一个“1”。

如果我们将右边的下一个位置也设为“1”，我们的总值将是 6410 + 3210，即 9610。这大于 8710，因此我们知道该位必须为“0”。

如果我们使下一个（16 位）位等于“1”，这将使我们的总值达到 6410 + 1610 或 8010，它更接近我们想要的值（8710），但不会超过它：

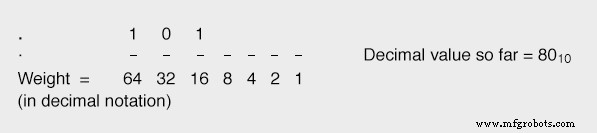
通过继续这个过程，根据需要设置每个较小权重的位以达到我们想要的总价值而不超过它，我们最终会得到正确的数字：

八进制和十六进制的试凑法

这种反复试验的策略也适用于八进制和十六进制转换。让我们取同样的十进制数字 8710，并将其转换为八进制数：

如果我们在 64 位放置一个“1”的密码，我们的总值为 6410（小于 8710）。如果我们在 64 位放置一个密码“2”，我们的总值为 12810（大于 8710）。这告诉我们，我们的八进制数必须在 64 位以“1”开头：

现在，我们需要在 8 位尝试使用密码值，以尝试获得尽可能接近 87 的总（十进制）值但不超过它。尝试前几个密码选项，我们得到：

8 位的密码值“3”将使我们超过所需的总数 8710，所以是“2”！

当然，如果你在上一节八进制/二进制转换的时候注意了，你会发现我们可以采用（十进制）8710 的二进制表示，我们之前确定它是 10101112，然后很容易地从它转换为八进制检查我们的工作：

我们可以用同样的方式进行十进制到十六进制的转换吗？当然可以，但谁愿意呢？这种方法简单易懂，但操作起来比较费力。

还有另一种方法可以进行这些转换，本质上是相同的（数学上），但更容易实现。

重复分割技术

另一种方法使用重复的除法循环（使用十进制表示法）将十进制数分解为二进制、八进制或十六进制位重值的倍数。

在第一个除法循环中，我们将原始十进制数除以我们要转换为的计数系统的基数（二进制 =2 八进制 =8，十六进制 =16）。

然后，我们取除法结果（商）的整数部分，再除以基值，依此类推，直到商小于1。

二进制、八进制或十六进制数字由每个除法步骤留下的“余数”确定。让我们看看这对二进制是如何工作的，以十进制的 8710 为例：

二进制位由连续除法步骤的剩余部分组合而成，从 LSB 开始，一直到 MSB。在这种情况下，我们得到一个二进制符号 10101112。

当我们除以 2 时，我们总会得到一个以“.0”或“.5”结尾的商，即余数为 0 或 1。如前所述，这种重复除法转换技术适用于计数二进制以外的系统。

如果我们使用不同的数字进行连续除法，例如 8 转换为八进制，我们必然会得到 0 到 7 之间的余数。让我们用相同的十进制数 8710 试试这个：

我们也可以使用类似的技术来转换处理数量小于 1 的计数系统。

为了将小于 1 的十进制数转换为二进制、八进制或十六进制，我们使用重复乘法，将每一步乘积的整数部分作为转换后数字的下一位。

我们以十进制数 0.812510 为例，转换为二进制：

与整数的重复除法过程一样，每一步都会为我们提供离“点”更远的下一个数字（或位）。

对于整数（除法），我们从 LSB 到 MSB（从右到左），但对于重复乘法，我们从左到右。

要将大于 1 的十进制数转换为 <1 分量，我们必须both 技术，一次一个。以十进制的54.4062510为例，转换成二进制：

相关工作表：

• 数字系统工作表