交流电路的一些例子

让我们将三个交流电压源串联起来，并使用复数来确定加性电压。

直流电路研究中学到的所有规则和定律也适用于交流电路（欧姆定律、基尔霍夫定律、网络分析方法），但功率计算（焦耳定律）除外。

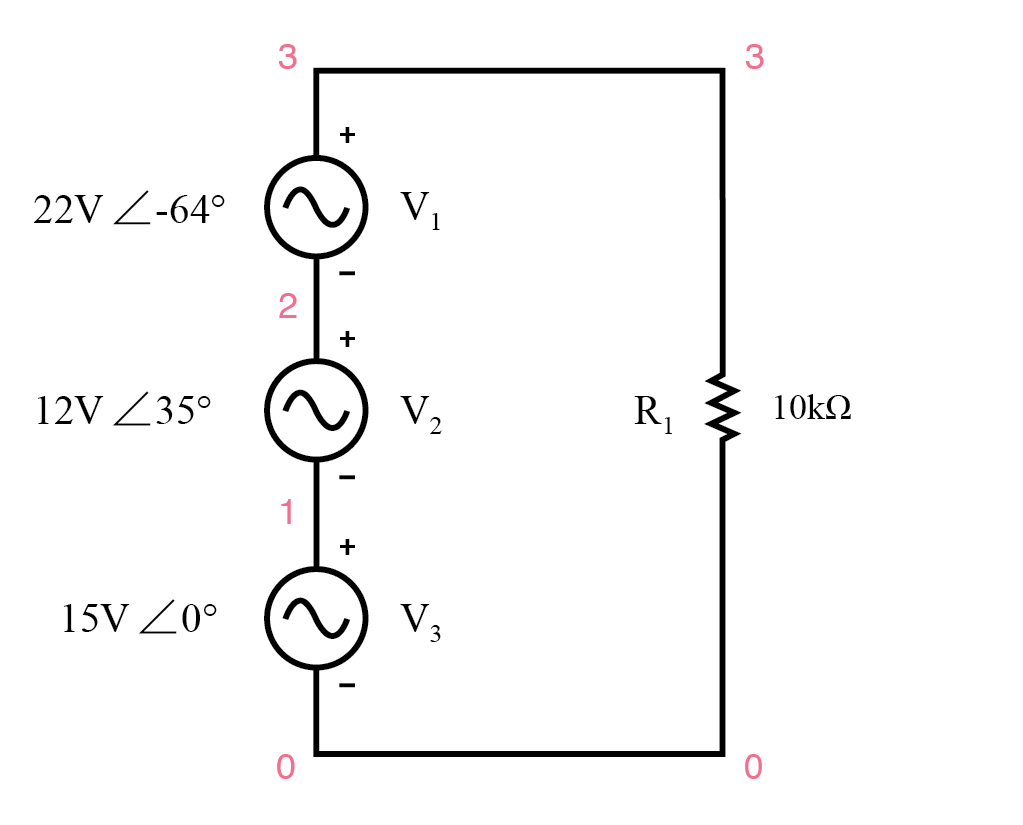
唯一的限制是所有变量必须 以复数形式表示，同时考虑相位和幅度，并且所有电压和电流必须具有相同的频率（以便它们的相位关系保持恒定）。 （下图）

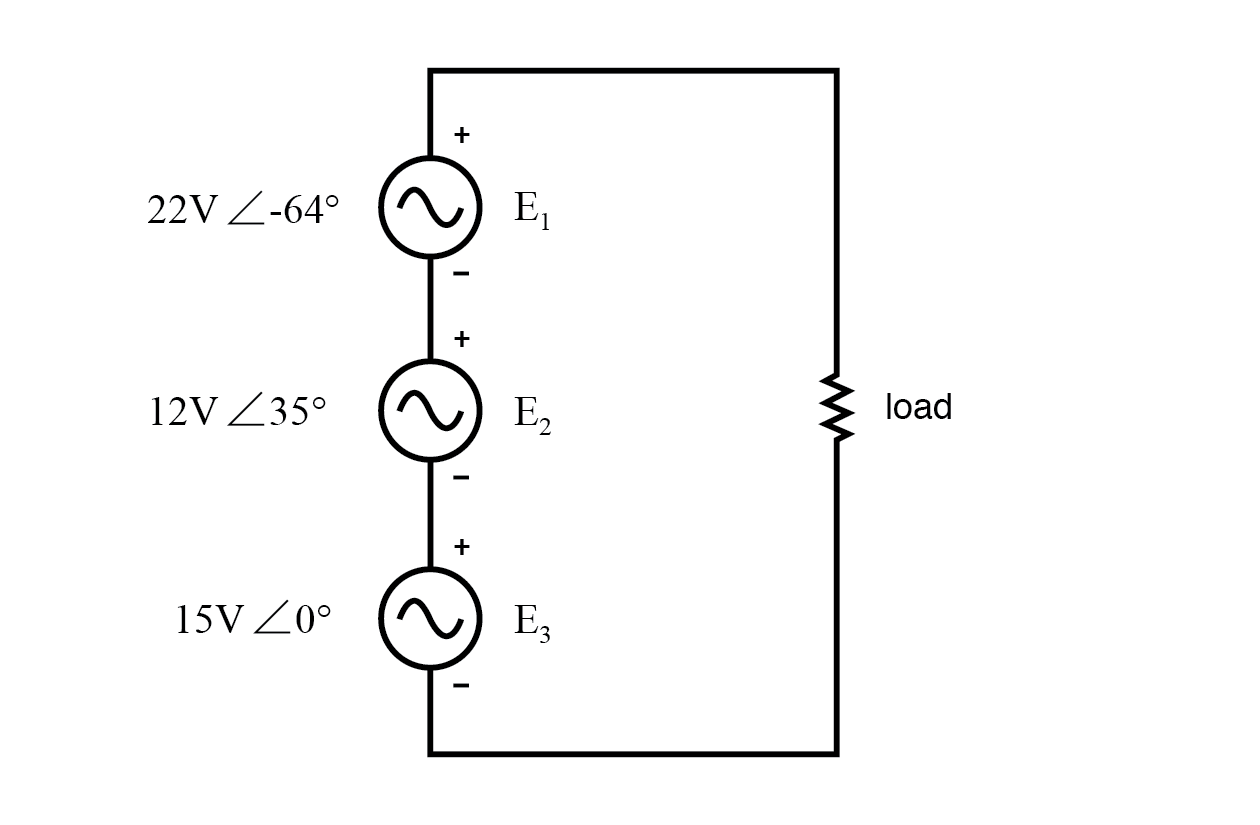
KVL 允许添加复杂的电压。

所有三个电压源的极性标记都以这样一种方式定向，即它们的规定电压应相加以形成负载电阻器上的总电压。

请注意，虽然为每个交流电压源给出了幅度和相位角，但没有指定频率值。如果是这种情况，则假定所有频率都相等，从而满足我们将直流规则应用于交流电路的条件（所有数字都以复数形式给出，所有频率都相同）。

我们求总电压的方程的设置如下所示：

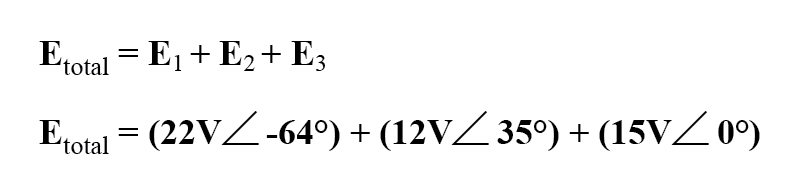
从图形上看，向量相加如下图所示。

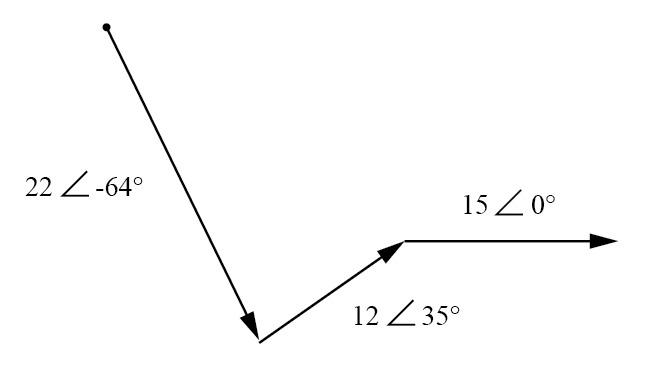
矢量电压的图形相加。

这些矢量的总和将是一个合成矢量，该矢量起始于 22 伏矢量的起点（图表左上角的点）并终止于 15 伏矢量的终点（中间的箭头尖端） -图右）：（下图）

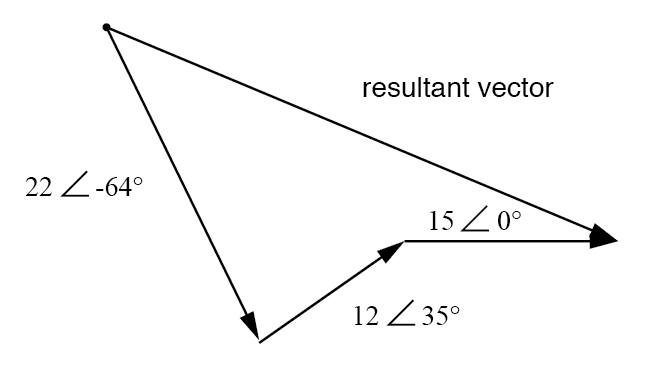
结果相当于三个原始电压的矢量和。

为了在不借助图形图像的情况下确定合成矢量的大小和角度是多少，我们可以将这些极坐标复数中的每一个都转换为矩形形式并相加。

请记住，我们正在添加 这些数字放在一起是因为三个电压源的极性标记以加法方式定向：

在极性形式中，这相当于 36.8052 伏 ∠ -20.5018°。这实际上意味着在这三个电压源上测得的电压将为 36.8052 伏，比 15 伏（0° 相位参考）滞后 20.5018°。

在实际电路中连接这些点的电压表只能指示电压的极性大小（36.8052 伏），而不是角度。示波器可用于显示两个电压波形，从而提供相移测量，但不能用于电压表。

交流电流表的原理也是一样的：它们表示的是电流的极值，而不是相角。

这对于将电压和电流的计算数字与实际电路联系起来非常重要。

虽然矩形符号便于加减法，并且确实是我们这里示例问题的最后一步，但它不太适用于实际测量。

矩形图形必须转换为极坐标图形（特别是极坐标magnitude )，然后才能与实际电路测量相关联。

我们可以使用 SPICE 来验证我们结果的准确性。在此测试电路中，10 kΩ 电阻值非常随意。这样 SPICE 就不会声明开路错误并中止分析。

此外，模拟频率的选择 (60 Hz) 是非常随意的，因为电阻器对所有交流电压和电流频率的响应都是一致的。还有其他组件（特别是电容器和电感器）对不同频率的响应不一致，但这是另一回事！ （下图）

Spice 电路原理图。

v1 1 0 ac 15 0 sin v2 2 1 ac 12 35 罪 v3 3 2 ac 22 -64 sin r1 3 0 10k .ac 链接 1 60 60 我使用的是 60 Hz 的频率 .print ac v(3,0) vp(3,0) 作为默认值 。结尾 频率 v(3) vp(3) 6.000E+01 3.681E+01 -2.050E+01 

果然，我们得到的总电压为 36.81 伏 ∠ -20.5°（参考 15 伏电源，其相位角任意表示为零度，以作为“参考”波形）。

乍一看，这是违反直觉的。如何在 15 伏、12 伏和 22 伏电源串联的情况下获得略高于 36 伏的总电压？使用直流电，这是不可能的，因为电压数字会直接增加或减少，具体取决于极性。

但是对于交流电，我们的“极性”（相移）可以在完全辅助和完全相反之间的任何地方变化，这就导致了这种矛盾的求和。

如果我们采用相同的电路并颠倒其中一个电源连接会怎样？它对总电压的贡献将与之前相反：（下图）

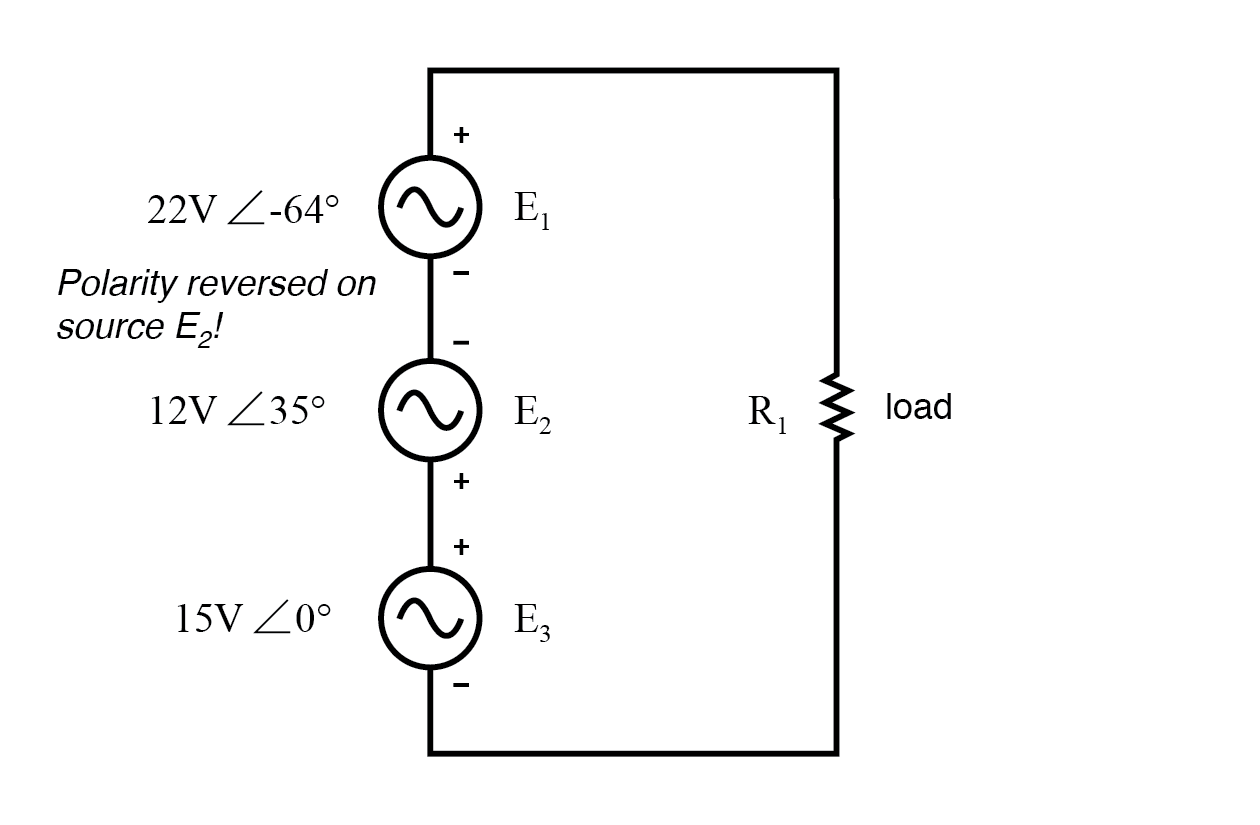
E2（12V）极性接反。

请注意 12 伏电源的相位角如何仍称为 35°，即使引线已颠倒。请记住，任何电压降的相位角都是根据其标注的极性来表示的。即使角度仍然写成 35°，向量也会被绘制成与之前相反的 180°：（下图）

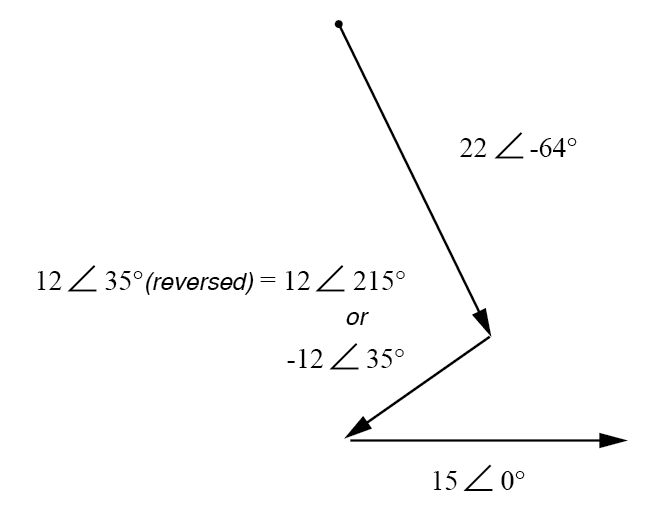
E2的方向反转了

所得（和）向量应从左上点（22 伏向量的起点）开始，并在 15 伏向量的右箭头尖端终止：（下图）

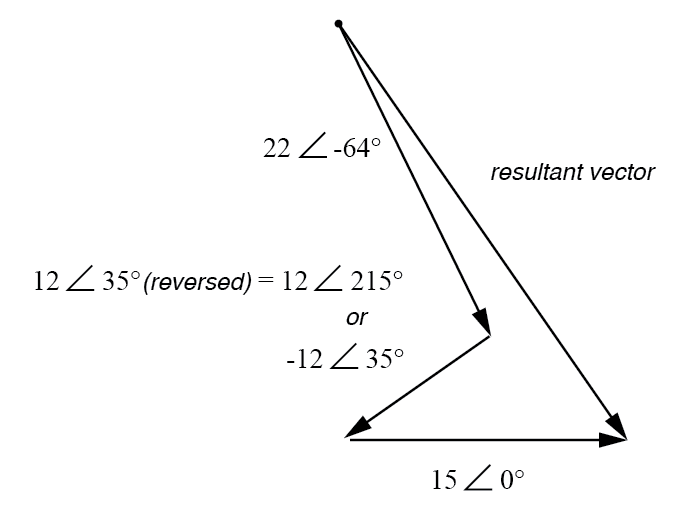
结果是电压源的矢量和。

12 伏电源上的连接反转可以用两种不同的极性形式表示：通过在其矢量角上增加 180°（使其成为 12 伏 ∠ 215°），或大小上的符号反转（使其 - 12 伏∠ 35°）。无论哪种方式，转换为矩形形式都会产生相同的结果：

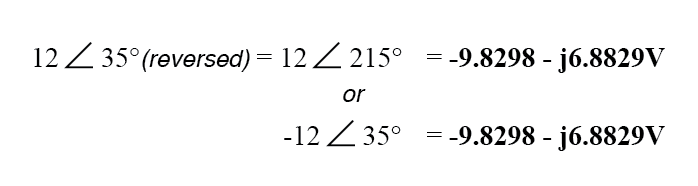
由此产生的矩形形式的电压相加，则：

在极坐标形式下，这相当于 30.4964 V ∠ -60.9368°。再一次，我们将使用 SPICE 来验证我们的计算结果：

交流电压加法 v1 1 0 交流 15 0 罪 v2 1 2 ac 12 35 sin 注意节点号 2 和 1 的颠倒 v3 3 2 ac 22 -64 sin 模拟连接交换 r1 3 0 10k .ac lin 1 60 60 .print ac v(3,0) vp(3,0) 。结尾 频率 v(3) vp(3) 6.000E+01 3.050E+01 -6.094E+01 

评论：

• 直流电路的所有定律和规则都适用于交流电路，但功率计算（焦耳定律）除外，只要所有值都以复杂形式表示和操作，并且所有电压和电流都处于相同频率.
• 当反转一个矢量的方向时（相当于反转一个交流电压源相对于其他电压源的极性），它可以用两种不同的方式来表示：角度加上 180°，或者反转大小的符号。
• 交流电路中的电表测量值对应于极坐标 的计算值。交流电路中复量的矩形表达式没有直接的经验等效项，尽管它们可以方便地执行加减法，正如基尔霍夫电压和电流定律所要求的那样。

相关工作表：

• 交流网络分析工作表
• 基尔霍夫定律工作表
• 欧姆定律工作表