米尔曼定理 - 分析交流和直流电路 - 示例

交流和直流电路的米尔曼定理 - 逐步解决示例

米尔曼定理

米尔曼定理在只有并联分支的电路分析中使用。因此，该定理可用于计算电路末端的电压。米尔曼定理只适用于包含并联网络的电路。

米尔曼定理是戴维南定理的组合 和 诺顿定理 .有时，这个定理也被称为 Parallel Generator Theorem .该定理由电气工程教授 Jacob Millman 提出 .并且以他的名字，这个定理被命名为米尔曼定理。

米尔曼定理指出；

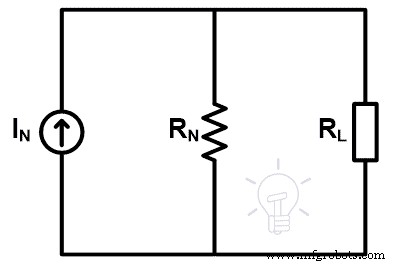
这意味着，我们可以找到给定网络的并行分支上的电压。当连接多个源时，该定理降低了网络的复杂度，如下图所示。

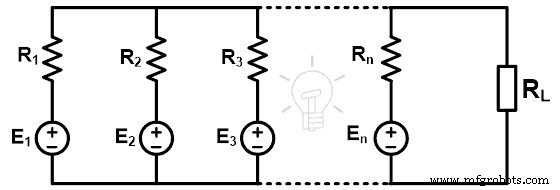
根据米尔曼定理；负载两端的电压为；

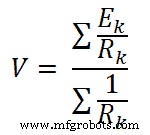
• 相关文章：戴维南定理。带有已解决示例的分步指南

数学方程式

如上图所示，电路有n个电压源（E1、E2、E3、...、En）。源极的内阻分别为R1、R2、R3、...、Rn。根据米尔曼定理，任何电路都可以用下面的网络代替。下图为米尔曼等效电路。

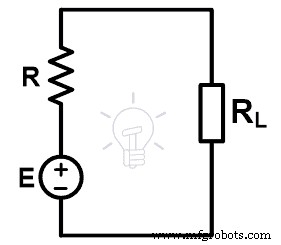
现在，我们需要找到电压源（E）和等效电阻（R）的值。上述电路类似于戴维南等效电路。因此，我们可以说电压源（E）与戴维南等效电压（VTH）相同，等效电阻为戴维南等效电阻（RTH）。

我们找到诺顿的等效电路来做一个简单的计算。为此，我们将进行源转换。并将所有电压源转换为电流源。

我们有一个与电压源串联的内部电阻。源极变换后，电压源变为电流源，内阻与电流源并联。因此，上述电路转换如下图所示。

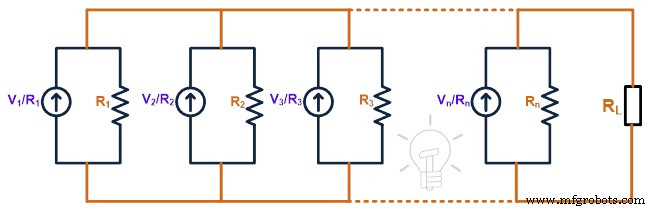
根据欧姆定律，电流源的值将是E1/R1, E2/R2, E3/R3, ..., En/Rn。现在，要找到诺顿的等效电流 (IN)，我们需要短接负载端子。并找到电流通过该分支。

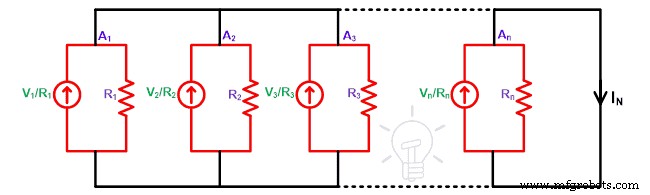
在节点A1，电流分成两条路径。一条路径通过电阻 R1，第二条路径来自短路支路。众所周知，电流总是流过低电阻路径。因此，在这种情况下，整个电流都通过短路的支路。并且通过电阻的电流为零。

节点 A2、A3、...、An 处的所有源都会发生同样的情况。并且通过所有电阻的电流为零。

现在，在节点 A2 处，添加来自节点 A1 的电流。类似地，在节点 A3 处，添加来自节点 A2 的电流。因此，在节点 An，来自所有节点的电流相加。总电流是所有电流的总和，称为诺顿电流 (IN)。

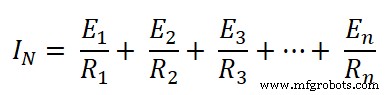
所以，我们找到了诺顿的等效电流。现在，我们需要找到诺顿的等效电阻。为此，我们需要通过开路电流源和短路电压源来消除电路中存在的所有能源。

在上图中，我们只有一个当前源。我们将通过开路去除这些电流源。我们需要移除负载来计算等效电阻。因此，剩下的电路如下图所示。

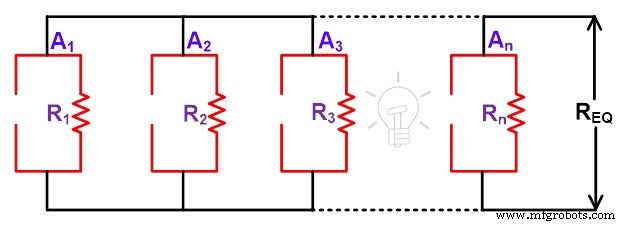
如上图，我们可以看到所有的电阻都是并联的。而这种并联组合就等于等效电阻。

请求 =RN =R 1 || R 2 || R 3 … || Rn

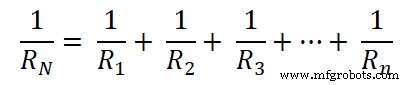
现在，将这些值放入下图所示的诺顿等效电路中。

如果我们把这个诺顿等效电路转换成戴维南等效电路，我们可以根据诺顿电流IN和诺顿电阻RN计算出E和R的值。

根据欧姆定律；

E =IN x RN

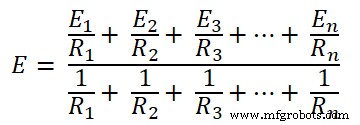
让我们将上面的等式做成n个分支的一般形式。

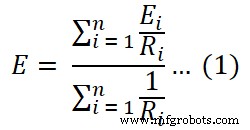
所以，我们得到了电压源的值。等效电阻的值等于诺顿的等效电阻。因此，我们可以得到米尔曼等效电路（图2）。

• 相关文章：诺顿定理。带有已解决示例的分步指南

米尔曼定理的步骤

步骤一 Milliman 定理仅适用于具有更多并行分支的网络或电路。因此，我们假设我们需要求解具有多个并联支路的电路，其中包含一个与内阻串联的电压源。

第二步 列出内阻或串联电阻及电压源。

第三步 求短路电压源负载端的等效电阻（R）。

第四步 应用米尔曼定理并找到负载端子上的电压 (E) 值。为此使用等式1。这个电压就是负载两端的电压。

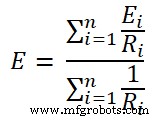
第五步 将 R 和 E 的值代入 Millman 等效电路（图 2）。

第六步 将KVL应用于回路，找出流过负载的电流。

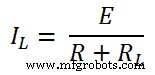
• 相关文章：叠加定理 - 带求解示例的电路分析

使用米尔曼定理分析直流电路

示例 #1

使用米尔曼定理求负载端的电流和电压。

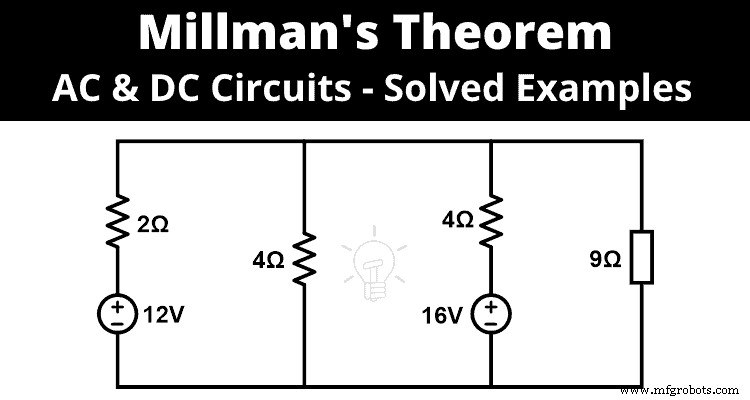
步骤一 通过观察上图，我们可以说所有四个分支都是并联的。我们可以应用米尔曼定理。

第二步 除了负载分支之外，还有三个分支。所以，下面列出了三个电压和三个电阻。

E 1 =12V 和 R 1 =2Ω

E 2 =0V 和 R 1 =4Ω

E 3 =16V 和 R 1 =4Ω

第三步 为了找到等效电阻，我们需要通过短路来移除电压源并打开负载端子。因此，剩下的图如下图所示。

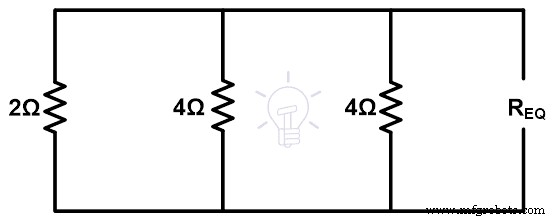
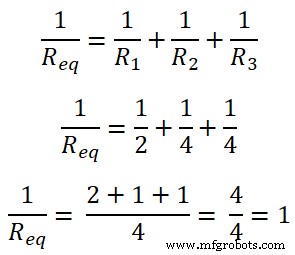
请求 =1Ω

如上图所示，所有电阻都是并联的。因此，等效电阻为；

第四步 现在，应用米尔曼定理。

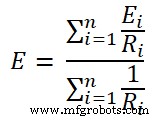
在这个例子中，我们有 3 个分支。因此，我们使用 n=3。

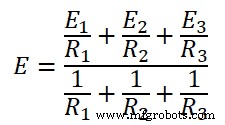
把上面列出的值代入这个方程。

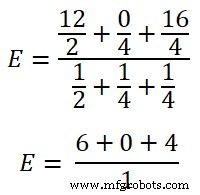
E =10V

这是负载端的电压。

第五步 将这些值放入米尔曼等效电路中。

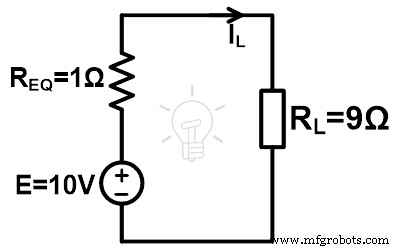
第六步 根据欧姆定律，

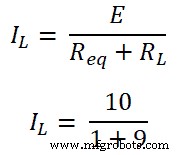
IL =1A

因此，负载两端的电压为10 V，通过负载的电流为1 A。

• 相关文章：Tellegen 定理 - 求解示例和 MATLAB 仿真

使用米尔曼定理分析交流电路

示例 #2

使用米尔曼定理求负载端子上的电流和电压。

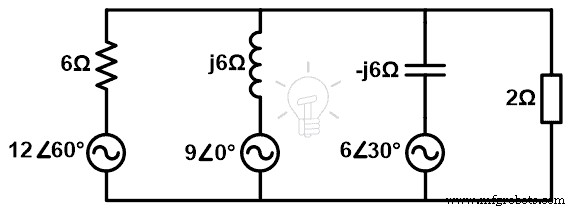
步骤一 如上图所示，四个支路并联。因此，我们可以应用米尔曼定理。

第二步 如果我们不考虑负载分支，则有三个分支。为了便于计算，我们将列出电压和阻抗。在交流电路的情况下，我们需要使用阻抗而不是电阻。

电压源的值以极坐标形式给出。但是，阻抗值以矩形形式给出。所以，我们需要将电压源的值转换成极坐标形式。

V 1 =12∠60° =6 + j 10.392

V 2 =9∠0° =9 + j 0

V 3 =6∠30° =5.196 + j 3

阻抗以矩形形式给出。所以，我们按原样列出。

Z 1 =6Ω

Z 2 =j 6Ω

Z 3 =–j 6Ω

第三步 求等效阻抗。如上例所示，我们需要通过短路来移除所有电压源。剩下的电路如下图所示。

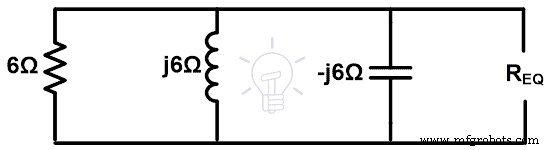
这里所有的阻抗都是并联的。因此，等效阻抗为；

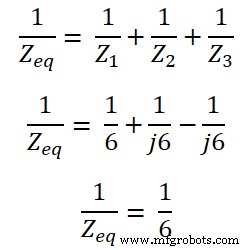
Z eq =6Ω

第四步 现在，应用米利曼定理，

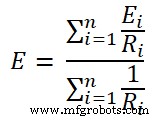
这里，我们有三个分支。因此，n等于3。

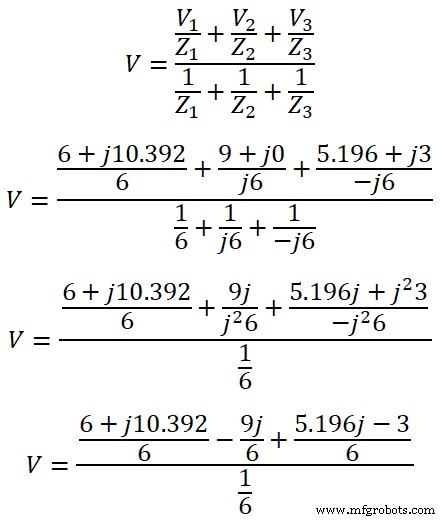
V =6 + 1j 0.392 - j 9 + j 5.196 - 3

V =3 + j 6.588

现在，我们需要找到 RMS 值。

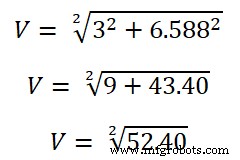
V =7.23V

第五步 将这些值放入米尔曼等效电路中。

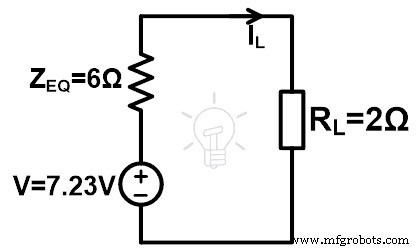
第六步 根据欧姆定律，

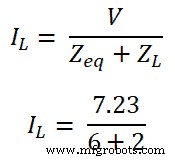
IL =0.9A

• 相关文章： 交流和直流电路的最大功率传输定理
  

米尔曼定理的局限性

米尔曼定理对求解网络很有帮助。但有一些限制如下。

• 该定理不适用于在独立源之间具有独立源的电路。
• 对于具有少于两个独立源的电路，该定理没有用处。
• 该定理不适用于只有串联元件的电路。
• 当源之间有元素连接时，该定理不适用。

米尔曼定理的应用

米尔曼定理在网络分析中广泛用于解决复杂电路。米尔曼定理的应用如下。

• Millman 定理最适用于在多个电压源提供更多并联支路的情况下找到负载阻抗的电压和电流。
• 这个定理的计算很容易。它不需要使用更多的方程。
• 该定理用于求解运算放大器等具有复杂元件的复杂电路。

相关电路分析教程：

• SUPERNODE 电路分析 - 逐步解决示例
• SUPERMESH 电路分析 - 逐步解决示例
• 基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
• 克莱默规则计算器 - 电路的 2 和 3 方程系统
• 惠斯通电桥——电路、工作、推导和应用
• 电气和电子工程计算器
• 5000 多个电气和电子工程公式和方程式