基材对 LSP 耦合波长和强度的影响

背景

局域表面等离子体 (LSP) 是贵金属纳米粒子 (NPs) 中的电子与入射光之间的强耦合现象，当 NPs 的大小与入射光波长相当或小于入射光波长时。 LSP 谐振波长取决于 NP 的尺寸、形状和材料以及周围的介电环境 [1,2,3,4]。由于其许多吸引人的特性，包括金属和电介质之间界面附近的电场呈指数增强，以及等离子体共振波长处的吸收增强 [5, 6]，LSP 已被集成到许多光电器件中，包括发光二极管 (LED) ) [7,8,9]、光电探测器 [10, 11]、太阳能电池 [12, 13] 和其他新兴技术，如表面增强拉曼散射 (SERS) [14,15,16,17]、tip-增强拉曼散射 (TERS) [18, 19] 和化学传感器 [20, 21]。

对于大多数基于 LSP 的应用，支持金属 NP 的基板是不可避免的。在以往的研究中，对基材影响的研究通常集中在基材的折射率或颗粒与基材之间的距离上[22, 23]。特别是对于具有立方几何形状的金属纳米粒子，基材会引起偶极和四极立方模式之间的杂化 [24, 25]。使用有效折射率理论忽略了基材的影响。然而，在我们之前的工作中，我们已经讨论了当半球形金属 NPs 位于基板上时，当光从不同方向入射时不同的 LSP 耦合强度，这可以归因于源自界面菲涅尔反射的不同局部电场强度[26]。在这项工作中，三种具有位于基板上的 Au NP 的结构用于 FDTD 模拟，以讨论 LSP 的耦合波长和强度。第一种结构是基板上的半球形金属纳米颗粒，可以通过物理方法获得，例如热退火或纳米压印 [27,28,29]。第二种结构是基底上的球形金属纳米颗粒，通常通过化学合成和后续转移过程获得 [30, 31]。这两种结构通常用于固体基材。第三种结构是半埋入基底的球形金属纳米颗粒，已在液-液界面上观察到 [32]。我们的结果表明，对于不同的结构，纳米颗粒周围介质的有效折射率表现不同。第一和第三结构的耦合波长随着衬底折射率的增加而发生很大的红移，而第二结构的耦合波长几乎保持不变。这可以归因于极化电场对基底的不同程度的渗透。此外，这三种结构的 LSP 耦合强度也已通过调整入射光的方向进行了研究，通常来自空气或基板。模拟结果表明，对于第一和第二结构，当光从不同方向入射时，散射峰强度的比值等于入射介质和出射介质的折射率之比。然而，对于第三种结构，这两个比率并不相等。这些行为可以通过使用修正的菲涅耳方程考虑 LSP 的局部驱动电场强度来定量解释。

然而，在实践中，通常会实现纳米粒子的阵列结构以进行研究。因此 NP 二聚体 [33,34,35] 也被用于讨论，因为周期性 NP 结构的近场特性将受到 FDTD 模拟中边界条件问题的影响。 FDTD 模拟结果表明，对于第一和第三结构，金属 NP 二聚体的耦合波长和强度的趋势与单一金属 NP 的趋势基本相似。然而，对于具有第二种结构的金属NP二聚体，基材折射率的影响略强于单一金属NP。

结果与讨论

图 1a-c 显示了 FDTD 模拟的结构示意图。图 1a 所示的结构代表介电基板上的半球形 Au NP，称为结构 A。图 1b 所示的结构代表介电基板上的球形 Au NP，称为结构 B。为了比较，图 1c 所示的结构 C 具有更高的对称性，也用于模拟。对于模拟，所有结构的 Au NP 的直径都设置为 60 nm。衬底上方介质的折射率设为n 在大多数情况下，1 =1。衬底的折射率从 n 变化 2 =1 到 n 2 =2.5。图 1d-f 分别显示了结构 A 到 C 的归一化散射光谱。可以清楚地看到，对于结构 A 和 C，随着基底折射率的增加，散射峰红移显着。然而，对于结构B，基底折射率的增加对散射峰的影响可以忽略不计。

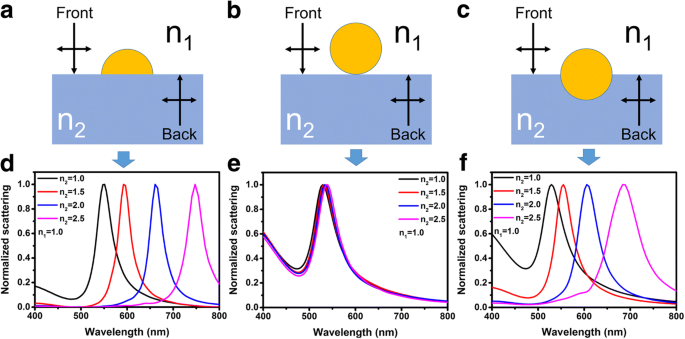
一 –c 分别用于FDTD模拟的结构A到C的示意图。 d –f 不同衬底折射率下结构A到C的归一化散射光谱

图 2a 显示了 LSP 散射最大值的波长与从图 1 中提取的基板的折射率。从图 2a 中，我们可以获得的第一个信息是，当基板的折射率增加时，散射峰值波长增加比线性假设更快。这可以用米氏理论大致解释。根据米氏理论，在准静态近似下，金属纳米颗粒被具有介电常数ε的各向同性非吸收介质包围的散射截面 米 可以表示为：

其中 k 是传播波的波矢，a 是球形金属 NP 的半径，ε 代表金属的介电常数。图 2a 中的插入显示了散射峰值波长与使用方程 2 计算的金属 NP 周围介质的折射率之间的关系。 (1).可以清楚地看到散射峰值波长和折射率之间的超线性关系，这与模拟结果非常相似。因此，我们可以使用有效折射率理论进行进一步讨论。从有效折射率理论，如果Au NP的散射峰值波长被折射率为n的无穷大电介质包围 效果 等于不同结构的Au NP，n 效果 可以看作是相应结构的有效折射率。表 1 显示了 n 效果 使用此方法获得。

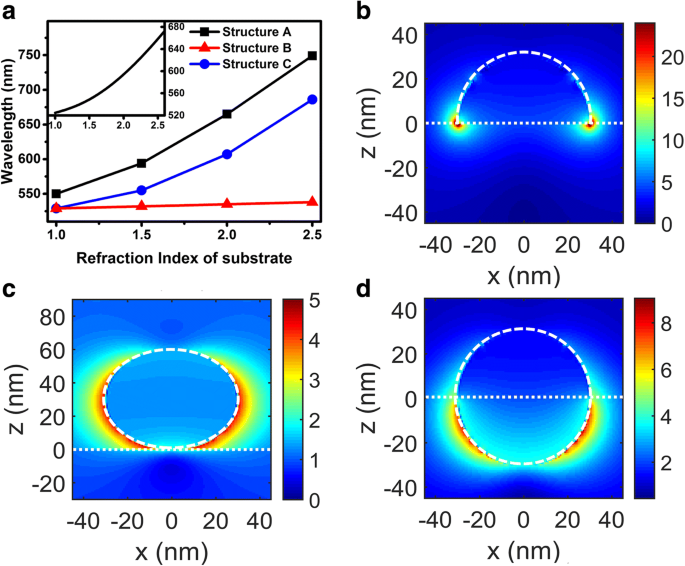
一 具有不同衬底折射率的不同结构的散射峰值波长。插图显示了基于 Mie 理论的 LSP 耦合波长与周围介质的折射率之间的关系。 b –d n 结构 A 到 C 的极化电场分布 2 =1.5分别在对应的LSP耦合波长处

使用线性拟合方程[36]：

其中 μ 可以作为加权系数来估计衬底折射率对LSP耦合波长的影响。可以估计界面上方和下方介质的影响。使用表 1 中所示的参数，加权系数 μ 结构A至C分别为0.38 ± 0.02、0.93 ± 0.01和0.25 ± 0.05。这些结果表明，对于结构 B，散射峰值波长几乎仅取决于界面上方介质的折射率。对于结构 C，衬底的折射率对散射峰值波长起着重要作用。然而，对于结构A，散射峰波长受界面上下介质折射率的影响。

这些现象可以通过电场分布分析来解释。图 2b-d 显示了具有 n 的结构 A 到 C 的电场幅度分布 2 =1.5 分别在相应的散射峰波长处。电场主要集中在界面附近，界面上方的介质和界面下方的介质分别影响结构 A 到 C 的 LSP 的共振波长。这些结果证实电场分布与计算的加权系数非常吻合，因为周围介质对散射峰值波长的影响可归因于局域电场引起的电介质极化。

从方程。 (2), 当 n 2 是固定的，n 1是可调的，变化率，即n的斜率 效果 , 是加权系数 μ .因此，如果基板不可避免，我们可以使用上述结果来优化基于 LSP 的化学传感器。基于LSP的化学传感器是通过LSP共振峰波长位移Δλ来检测周围环境的折射率变化 [37]。传感器的灵敏度与两个参数密切相关，包括位移参数S =d (Δλ )/d (Δn ) 和品质因数 FOM =S /半高宽 , 其中 Δn 表示折射率和FWHM的变化 是初始状态半高处的全波 [37, 38]。以前关于基于 LSP 的传感器的大多数研究都集中在 NPs 的材料、尺寸和形状上 [39,40,41]。然而，很少有报告讨论底物的影响及其与金属纳米颗粒的相互作用。图 3 显示了当 n 时结构 A 到 C 的散射光谱 1 从 1.0 线性增加到 1.5 并且 n 2 固定为 1.5 或 2.5。所有图中的插入物代表散射峰值波长 vs. n 1. 图 3a-f 显示 S 结构A和B的参数高于结构C。表2列出了S的计算参数 , 半高宽 , 和 FOM 来自图 3。对于 n 2 =1.5，S 和 FOM 结构 A 和 B 的参数比结构 C 的参数要好得多。但是，对于 n 2 =2.5，虽然S 结构 A 和 B 的参数高于 n 时的参数 2 =1.5，FOM 由于 FWHM 的增加而恶化 .

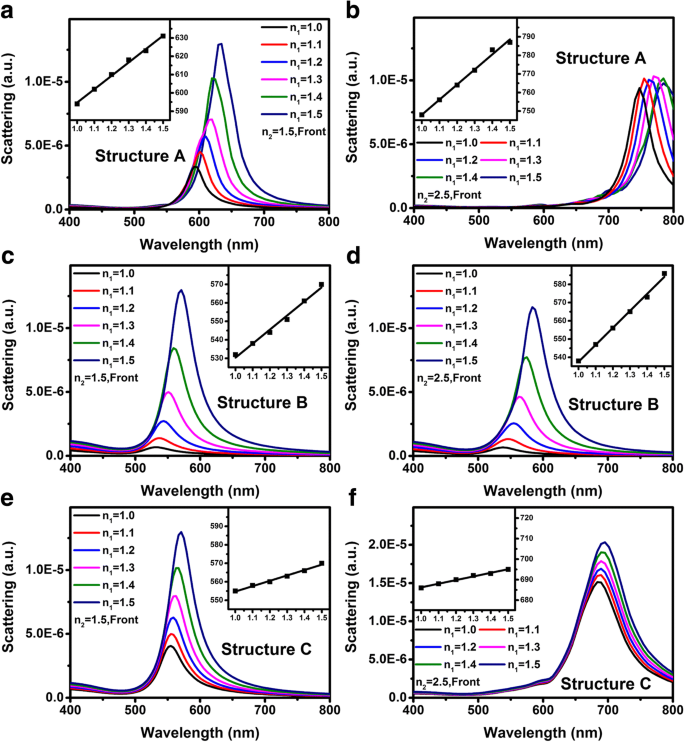
一 , c , e n时结构A到C的散射光谱 1 从 1.0 线性增加到 1.5。固定 n 分别为 2 =1.5。 b , d , f n时结构A到C的散射光谱 1 从 1.0 线性增加到 1.5，固定 n 分别为 2 =2.5。插图显示了散射峰值波长与 n 之间的关系 1 对于不同的结构或基材的折射率

上面的讨论都是关于 LSP 耦合波长的。同时，LSP 耦合强度是许多基于 LSP 的设备（如 LED、光电探测器、太阳能电池）和新兴技术（如 SERS、TERS 和化学传感器）的另一个有价值的参数。我们之前的研究表明，对于结构 A，光和 LSP 之间的耦合强度会受到光入射方向的影响。这可以归因于光从空气和基板正常入射时不同的局部驱动电场强度 [26]。光从基板入射（表示为背入射）和空气（表示为前入射）时消光峰强度的比值C B /C F 等于 n 2/n 1. 图 4 显示了光从不同方向入射时的 FDTD 模拟散射光谱，与被相应有效折射率包围的 Au NP 的散射光谱相关。图 4a-c、d-f 分别表示结构 A 和 C 的散射光谱。衬底的折射率 n 对于图 4a、d、b、e、c、f，图 2 分别为 1.5、2.0 和 2.5。 n 对于所有光谱，1 固定为 1.0。与消光光谱相似，光从前后入射时的散射峰强度C SB /C SF 等于 n 2/n 1 对于结构 A 和 C。

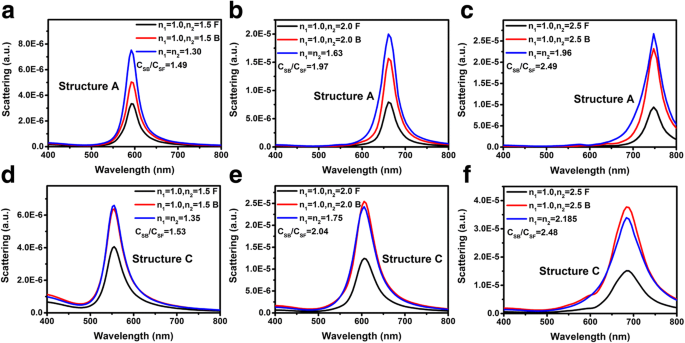
不同 n 的散射光谱 结构 A (a –c ) 和结构 C (d –f ） 分别。光通常从空气（用黑线表示）和基材（用红线表示）入射。蓝线表示Au NPs被具有有效折射率的无限电介质包围的散射光谱

当我们考虑被相应有效折射率包围的 Au NP 的散射光谱时，结构 A 和 C 的散射峰强度之间存在差异。图 5a、b 显示了 C 的比率 SF /C 塞夫 和 C SB /C 塞夫 分别与结构 A 和 C 基材的折射率对比，其中 C 塞夫 是散射峰强度，Au NP 被具有有效折射率的无限电介质包围（图 4）。对于所有底物，比率 C SF /C 塞夫 和 C SB /C 塞夫 结构A比结构C小。这也可以用结构A和C的局部驱动电场不同来解释。

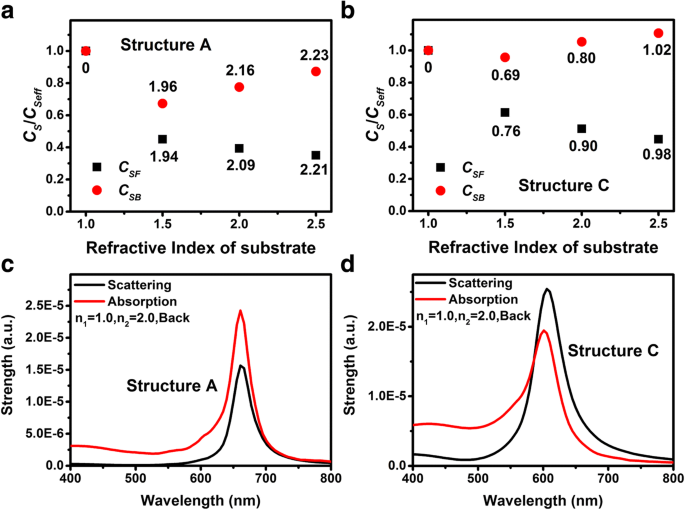
一 , b 耦合强度比C S /C 塞夫 与各种 n 分别为结构A和结构C的2。黑色矩形和红色圆点分别代表正面和背面的事件案例。 c , d 固定 n 结构 A 和 C 的散射和吸收光谱 2 =2.0 当光从基板入射时

基于修正的菲涅尔方程[26, 42]，光从正面和背面入射时的局部驱动电场强度可写为 2n 1E 我 /(n 1 + n 2 + A ) 和 2n 2E 我 /(n 1 + n 2 + A )，其中 E 我 是入射波的电场强度，A =− i (ω /c )ρα 可以看作是由 LSP 产生的附加参数，它与极化率 α 成正比 Au NPs 并且在 LSP 共振频率下是一个正实数。因此 C SB /C SF 等于 n 2/n 1 也显示在图 4 中。另一方面，当Au NPs被相应的有效折射率包围时的局部驱动电场强度等于E 我 .因此 A 的值 参数可以使用以下公式获得：

计算出的 A 参数列在图 5a、b 中相应点附近。可以看出 A 的值 非常接近，但对于不同的光入射方向并不完全相同。这归因于 C 之间的细微差别 SB /C SF 和 n 2/n 1 以及仿真软件的准确性。对于具有不同衬底折射率的相同结构，A 值随着衬底折射率的增加而增加，这可归因于随着 LSP 共振波长的增加，Au NP 的极化率增加 [43,44,45]。另一方面，人们应该意识到 A 对于具有相同衬底折射率的不同结构，结构 A 的值远大于结构 C 的值。这意味着结构 A 的 Au NPs 的极化率远大于结构 C 的极化率，这可以由图 2b、d 证明。有趣的是，虽然结构 A 的 Au NPs 的极化率大于结构 C，但结构 A 的散射峰强度小于结构 C（图 4）。这可归因于结构 A 的较高吸收。图 5c、d 分别显示了结构 A 和 C 的散射和吸收光谱，两种结构的基板的折射率均为 2.0，光从背面入射。可以看出结构A的吸收远高于结构C。因此对于结构A，激发LSP的大部分能量是通过吸收消耗的，没有发生散射。

然而，对于结构 B，比率 C SB /C SF 不等于 n 2/n 1. 图 6a-c 显示了结构 B 的散射光谱，其基底折射率分别为 1.5、2.0 和 2.5。 C SB /C SF 结构 B 小于 n 2/n 1 对于所有基材折射率。如图 6d 示意性所示，当光从正面入射时，局部驱动电场可以写为 E 的叠加 我 和 E rF , 其中 E rF 是反射波的电场强度。光从正面入射时的局部驱动电场强度可写为 \( {E}_{dF}={E}_i+{E}_{rF}=\left[1+\frac{n_1- {n}_2}{n{}_1+{n}_2}\cos \left(\frac{4\pi Pa}{\lambda_{LSP}}\right)\right]{E}_i \)，其中 P 是与光通过 Au NPs 传播时振荡电子的平均距离和附加光路相关的系数，λ LSP 是 LSP 的共振波长。考虑到光从背面入射时的局部驱动电场强度可以写成E 分贝 =E tB =2n 2E 我 /(n 1 + n 2)、光从背面和正面入射时局部驱动电场强度的比值可写为：

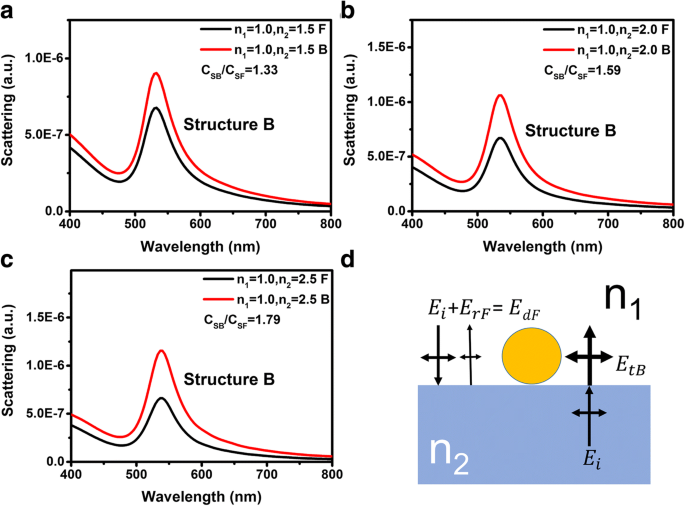
一 –c 不同 n 的散射光谱 结构B的2 =1.5、2.0和2.5。黑线和红线分别代表前后事件案例。 d 不同入射方向下结构B局部驱动电场示意图

表 3 列出了 C SB /C SF 由散射光谱和E得到的结构B 分贝 /E dF 使用公式计算。 (4) 用不同的P 系数。可以看出，当 P 系数等于 1.5，E 分贝 /E dF 与C的比例吻合 SB /C SF 适用于所有基材。 P 的原因 等于1.5还不清楚。

表 4 和表 5 列出了 C SB /C SF 由散射光谱和E得到 分贝 /E dF 使用公式计算。 (4) 用不同几何结构和材料的纳米粒子来研究P的普遍性 系数。可以看出，对于不同尺寸的 Au NP，当 P 系数等于1.5，C的比值 SB /C SF 和 E 分贝 /E dF 每当 NPs 是扁椭圆形或长椭圆形时，彼此都非常一致。表 5 表明 P 不同尺寸的Ag NPs的系数也等于1.5。因此 P 系数比较普遍，说明P应该有内在机制 系数，值得进一步深入研究。

以上讨论基于单个 NP。然而，在实践中，通常会实现纳米颗粒的阵列结构以进行研究。因此，应该使用 NP 二聚体进行讨论，因为周期性 NP 结构的近场特性将受到 FDTD 模拟中边界条件问题的影响。用于二聚体模拟的 NP 的几何结构参数与上面讨论的单个 NP 的几何结构参数相似，并且在这两个 NP 之间设置了 2 nm 间隙。模拟结果（此处未显示）表明，当垂直入射光的偏振方向垂直于 NP 二聚体时，所有特性与单个 NP 所示的相同。因此，下面讨论的所有近场特性都基于偏振方向平行于 NP 二聚体的入射光。

图 7a、b 分别显示了介电基板上的半球形 Au 二聚体（结构 A'）和半埋入基板中的球形 Au 二聚体（结构 C'）的示意图。图 7c、d 显示了具有不同基板折射率和光入射方向的二聚体的散射光谱。可以看出，对于结构 A' 和 C'，在所有光谱中均观察到一阶和二阶散射峰。特别是，对于结构C'，当衬底的折射率等于2和2.5时，可以观察到三阶峰。还可以看到所有散射峰都随着衬底折射率的增加而发生很大的红移。这可以通过结构 A' 和 C' 的一阶峰的相应波长处的电场幅度分布来解释，分别如图 8a、b 所示，衬底的折射率为 1.5。与图 2 类似，电场主要集中在界面附近。因此，当光从不同方向入射时，C SB /C SF n 2/n 1 是可以预期的，如图 7c、d 所示。另一方面，与图 4 所示的散射光谱相比，二聚体的散射峰强度远高于单个 NP 的散射峰强度。这归因于热点的巨大电场增强 在纳米间隙[33]。

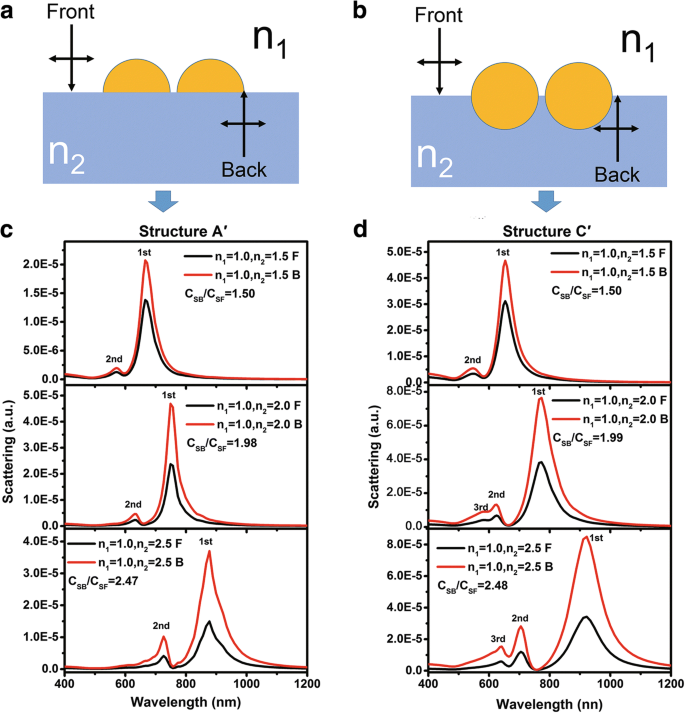
一 , b 分别用于FDTD模拟的结构A'和C'的示意图。 c , d 不同 n 的散射光谱 结构A'和结构C'的2 =1.5、2.0和2.5。光从空气（黑线）和基板（红线）正常入射

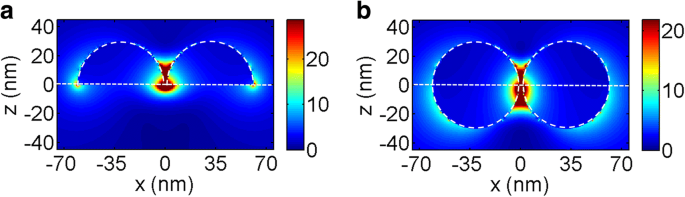
一 , b n结构A'和C'的极化电场分布 2 =1.5分别在一阶峰的对应波长处

然而，如图 9 所示，对于位于电介质基底上的球形 Au 二聚体（结构 B'），基底折射率的影响略强于结构 B。一阶峰红移从 580当基板的折射率从 1.5 增加到 2.5 时，增加到 614 nm，其中大于单个 NP 的折射率（从 532 到 538 nm）。这可能归因于结构 B' 的一阶峰值的相应峰值波长处的电场幅度分布（图 9d，衬底的折射率为 1.5）。基板中的电场强度比图 2c 中所示的强。同样，如图 9 所示，C 的比率 SB /C SF 对于结构 B' 的 NP 二聚体不等于 n 2/n 1，类似于单个NP。然而，P 参数不再是常数，如果方程。 (4) 仍然适用。 P 当基板的折射率分别为 1.5、2.0 和 2.5 时，计算参数分别为 1.67、1.82 和 2.05。 P 之间的区别 结构B和B'的参数需要进一步研究。

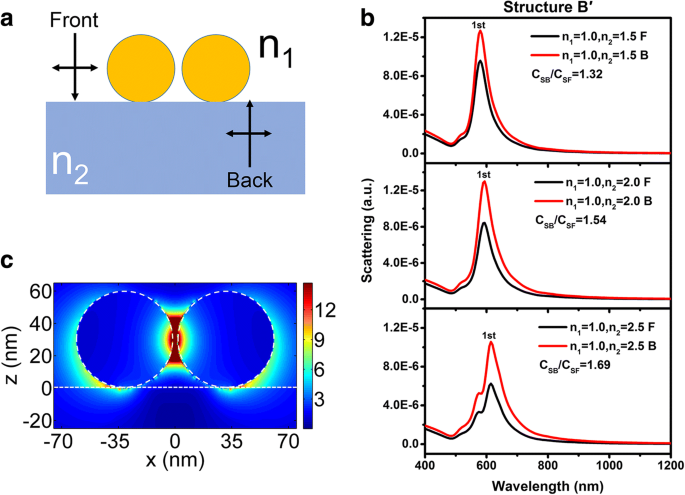
一 用于FDTD模拟的结构B'的示意图。 b 不同 n 的散射光谱 结构B'的2 =1.5、2.0和2.5。光通常从空气（用黑线表示）和基材（用红线表示）入射。 c 具有n的结构B'的极化电场分布 2 =1.5 在 532 nm

结论

综上所述，通过FDTD模拟和理论分析，研究了衬底对LSP耦合波长和强度的影响。对于半球形Au NPs位于衬底上且球形Au NPs半埋入衬底的结构，LSP耦合波长随衬底的折射率变化很大。然而，对于球形 Au NPs 位于衬底上的结构，LSP 耦合波长对衬底的依赖性是微不足道的。依赖差异可以用不同结构的 LSP 的极化场分布来解释。对于球形Au NPs半埋入衬底的结构，LSPs的极化场集中在衬底上方的介质中。然而，对于其他两种结构，极化场极大地渗透到衬底中。此外，还通过改变光的入射方向（通常来自空气或基板）来研究这三种结构的 LSP 耦合强度。模拟结果表明，对于半球形纳米颗粒位于衬底上和球形纳米颗粒半埋入衬底的结构，不同光入射方向的散射峰强度之比等于入射介质的折射率与退出介质。然而，对于球形纳米颗粒位于基板上的结构，这两个比例并不相等。通过使用修正的菲涅耳方程考虑 LSP 的局部驱动电场强度，已经对这些现象进行了定量解释。还计算了 NP 二聚体的近场特性。尽管散射光谱中显示了多级峰，但对于具有基底折射率的结构，位于基底上的半球形 Au 二聚体和半埋入基底中的球形 Au 二聚体的散射峰波长红移很大。不同光入射方向的散射峰强度之比也等于入射介质和出射介质的折射率之比。然而，对于位于衬底上的Au二聚体，衬底折射率的影响略强于位于衬底上的单个球形Au NP。

方法

The models of hemi-/spherical metal NP located on substrate (denoted as structures A and B) and spherical metal NP half-buried into substrate (denoted as structure C) are created and studied by Lumerical FDTD (version 8.15.736), a commercial finite-difference time-domain solver. The substrate is semi-infinite in the z axis and infinite in the x /y 轴。 The size of NP is set as 60 nm in diameter. The refractive index parameter of metal, gold, and silver specifically are support by CRC [46]. Total-field scattered-field source (TFSF), a special designing light source for studying particle scattering, is adopted in our research. The light normally incident from + z direction (designed as front incident) and − z direction (designed as back incident). Perfectly matched layers (PMLs) were used to absorb the scattered radiation in all directions (in order to eliminate reflection back to the model). The PML parameters such as Kappa, Sigma, layers, and polynomial order are assumed by 2, 1, 32, and 3 respectively. In addition, FDTD method consists in introducing a space and time mesh that must satisfy the stability criterion [47]. In order to converge, the simulation time and time steps (dt) are set to 2000 fs and 0.07 fs respectively. The space mesh is set to 0.3 nm in every direction (dx  = dy  = dz ).

缩写

FDTD：

有限差分时域

LSP:

Localized surface plasmon

NP：

纳米粒子

SERS:

Surface-enhanced Raman scattering

TERS:

Tip-enhanced Raman scattering

TFSF：

全场散场