带有 V 形槽腔的通道等离子体纳米线激光器

背景

凭借圆柱形几何形状和对电子、空穴和光子的强二维限制，独立的半导体纳米线是具有降低阈值和紧凑尺寸的半导体激光器的理想选择 [1,2,3,4,5,6]。迄今为止，室温激光发射已经在 ZnO、GaN、CdS 和 GaAs 纳米线中实现，涵盖了从紫外到近红外的光谱 [7,8,9,10,11,12]。为了继续缩小纳米线的尺寸超出衍射极限，已经提出并实验证明了等离子体纳米线激光器，包括混合等离子体纳米线激光器和高阶模式等离子体纳米线激光器 [13,14,15]。其中，混合等离子体纳米线激光器实现了更小的尺寸限制。最近，等离子体纳米线激光器显示出其与等离子体波导集成的能力，在 V 型槽等离子体波导中使用通道等离子体极化 (CPP) 模式 [16]。实验中采用的直径在 300 nm 以上。 CPP 是由雕刻在金属上的 V 形凹槽引导的等离子体激元，这是由 Maradudin 及其同事首先在理论上提出的 [17]。 CPPs在近红外波长下表现出强约束、低阻尼和抗通道弯曲的鲁棒性[18,19,20]。

在这里，通过将混合等离子体模式的低耗散与 CPP 模式的等离子体波导的强限制和集成相结合，我们提出了一种混合通道等离子体纳米线 (CPN) 激光器，并数值研究了模式和激光特性。 CPN 激光器由核壳型 GaAs/AlGaAs 纳米线和银 V 型槽组成，由超薄的 MgF2 介电层隔开，其中纳米线的直径在 40 到 220 nm 范围内，以探索超出衍射极限的激光特性。由于GaAs/AlGaAs纳米线的六边形形状，下一节将展示CPN激光器的两种集成结构。

PPN 激光结构

CPN 激光结构示意图如图 1 所示，其中背景材料为空气，灰色材料为银，其介电常数由 Drude 模型描述 \( {\varepsilon}_r={\varepsilon}_{ \infty }-{\omega}_p^2/\left({\omega}^2+ j\gamma \omega \right) \)，与 ε ∞=3.7，ω p =9.1 eV 和 γ =0.018 eV [21]。铺设在V型槽中的纳米线具有核壳结构，核材料为GaAs，壳材料为AlGaAs。 GaAs 核被 10 nm 的薄 AlGaAs 壳层钝化，以提高辐射效率 [12]。在纳米线和 V 形槽之间是一层超薄的 MgF2 介电层。其厚度固定为 5 nm，以支持在强光限制下的低损耗传播。 CPN激光器有两种集成方式。第一个我们称之为 CPN-N（CPN-narrow-angle），如图 1a、c 所示，其中纳米线以 60° 的窄角水平放置在 V 型槽的表面上。纳米线有两侧接触介质层和V型槽表面，底面和V型槽的顶点之间是空气。第二个我们称之为 CPN-W（CPN-广角），如图 1b、d 所示，其中纳米线垂直铺设在 V 型槽表面，广角为 120°。纳米线不仅有两侧接触，而且还与介电层和V型槽表面有顶点接触。

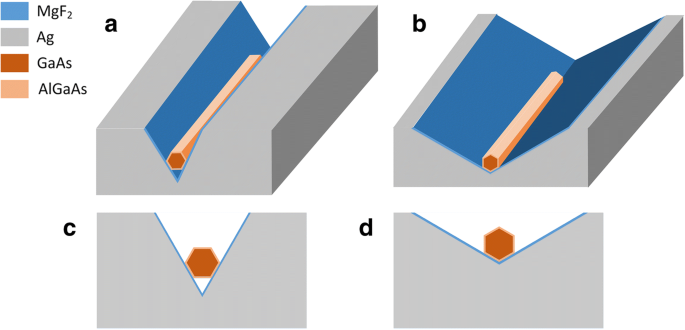
CPN激光器结构示意图。 一 CPN-N。 b CPN-W。 c CPN-N 的横截面。 d CPN-W截面

V型槽中支持的CPP模式取决于槽的角度和深度，尤其是角度。通常，凹槽支持的 CPP 模式数量随着角度的增加而减少，并且在有限深凹槽中，如果度数大于临界度，则凹槽中不能存在 CPP [22]。在角度足够小的凹槽中可以实现 CPP 的强定位 [23]，如图 2 所示。在图 2a-c 中，凹槽深度固定为 1 μm，凹槽角度为 10° 、 30° 和 60° 分别。电场强烈集中在凹槽底部 10°，形成 CPP 模式。而电场开始向凹槽边缘分布 30°，表明定位变得更弱。随着凹槽角度增加到60°，凹槽不存在CPP。然而，如图 2d、e 所示，随着纳米线的集成，CPP 仍然以 60° 和 120°（深度小于 1 μm）的广角存在，并紧密地定位在低介电 MgF2 层内，这是完全不同于普通的凹槽。在像 CPN 腔这样的混合等离子体结构中，跨越超薄电介质层的电介质和等离子体模式之间的耦合实现了“类似电容器”的能量存储，允许亚波长光在具有纳米局部电磁场的非金属区域中传播 [24]。因此，CPP 的电场强烈地集中在纳米线和凹槽之间的 MgF2 间隙中，即使在大角度的凹槽中也是如此。 CPN-N 和 CPN-W 激光器的进一步引导和激射特性将在下一节详细说明。

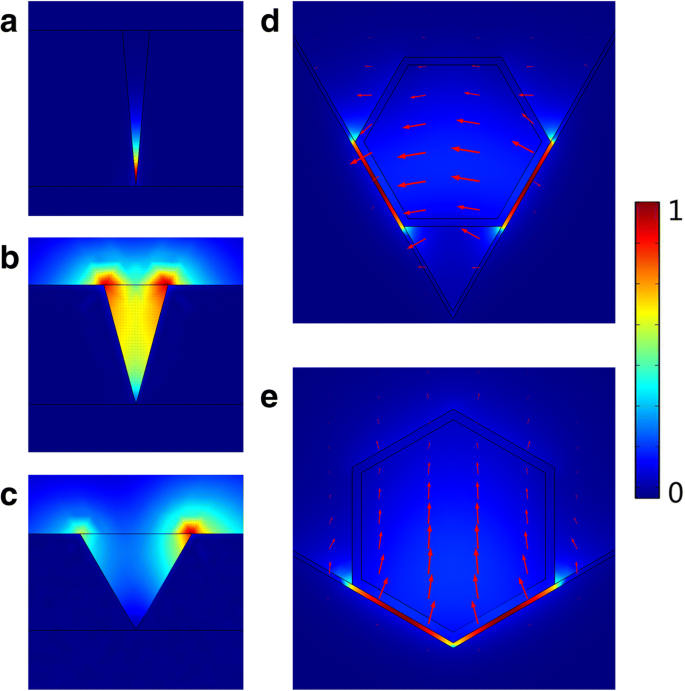
a 中的电场分布 10° 的凹槽。 b 30° 的凹槽。 c 60° 的凹槽。 d CPN-N 激光器。 e CPN-W 激光器。红色箭头表示电场方向

结果与讨论

凭借混合等离子体模式的优势，电场可以定位在超出衍射极限的尺寸，并具有低损耗传播 [25, 26]。因此，我们的研究集中在 40 到 220 nm 亚波长直径尺寸的引导和激光特性。尽管精确控制直径小于 100 nm 的纳米线的位置具有挑战性，但这里考虑或多或少的理想条件来探索 CPN 激光器的潜在性能。

与其他等离子体纳米线激光器一样，随着纳米线直径的增加，CPN 激光器支持更多的导模。如图 3 所示，包含在凹槽中的直径为 200 nm 的纳米线可以支持四种导模，HE11x、HE11y、TE01 和 TM01。凹槽表面平行于纳米线的侧面，因此凹槽角度随着纳米线直径的变化而保持不变。在具有平面衬底的等离子体纳米线激光器中，纳米线只有一侧与衬底接触，导致仅在 HE11y 的光子模式和表面等离子体激元之间耦合。而在 CPN 结构中，由于纳米线和凹槽表面之间的两侧接触，HE11x 和 HE11y 都与表面等离子体耦合形成混合通道等离子体模式。对于模式 TE01 和 TM01，纳米线内部的电磁能也与凹槽表面上的表面等离子体耦合，形成通道等离子体模式。以上四种模式是直径为200 nm的CPN激光器中的导模，随着直径的减小而截止。

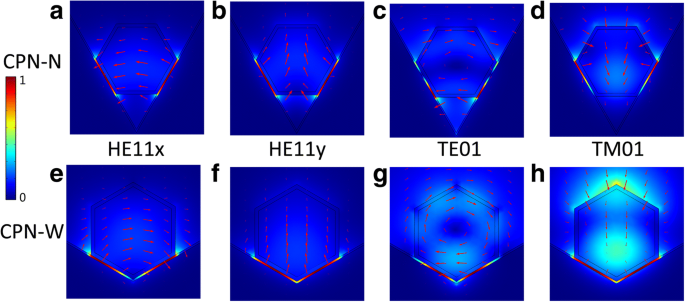
CPN-N激光器模式电场分布(a –d ) 和 CPN-W 激光 (e –h ）。纳米线直径固定为 200 纳米

研究 CPN 激光器的引导和激光特性、有效折射率实部、模态损耗、模态限制因子和阈值增益对纳米线直径的依赖性 D 计算并显示在图 4a-d 中。这里研究了 CPN-N 和 CPN-W 激光器的 HE11x、HE11y、TE01 和 TM01 模式。 CPN-N和CPN-W激光器的特性分别用实线方框符号和虚线圆圈符号表示。值得注意的是，这里的凹槽深度远大于纳米线直径，以消除凹槽边缘的影响。如图 4a 所示，有效指数 Re(n eff) 和纳米线直径 D .这与单个纳米线的有效指数表现相同。随着纳米线直径的增加，结构的等效指数变大，导致模态指数增加。随着直径的减小，CPN-W激光器的TE01模首先在200nm处截止，然后CPN-W激光器的TM01模在180nm处截止，CPN-N激光器的TE01和TM01模都在170nm处截止，而基模 HE11x 和 HE11y 具有较小的截止直径。由于CPN激光器的非对称结构，基模不再退化。在 CPN-N 激光器的所有模式中，HE11x 模式的最小截止直径为 40 纳米。在 CPN-W 激光器的所有模式中，HE11y 模式的最小截止直径为 80 nm。在 CPN-N 激光器中，Re(n HE11x 模式的 eff) 大于 HE11y 模式。而在 CPN-W 激光器中，Re(n HE11y 模式的 eff) 大于 HE11x 模式，这是由基本模式的垂直分量产生的。通常情况下，HE11x 和 TE01 的电场方向分别垂直于 HE11y 和 TM01。在 CPN-N 和 CPN-W 激光器中，凹槽角度为 60° 和 120°，导致 x -模式分量在 CPN-N 激光器和 y 中占主导地位 - 模式分量在 CPN-W 激光器中占主导地位，如图 2d，e.因此，模式 HE11x 和 TE01 具有更大的 Re(n eff) 和 CPN-N 激光器中更小的截止直径，而 HE11y 和 TM01 模式具有更大的 Re(n eff) 和更小的 CPN-W 激光器的截止直径。

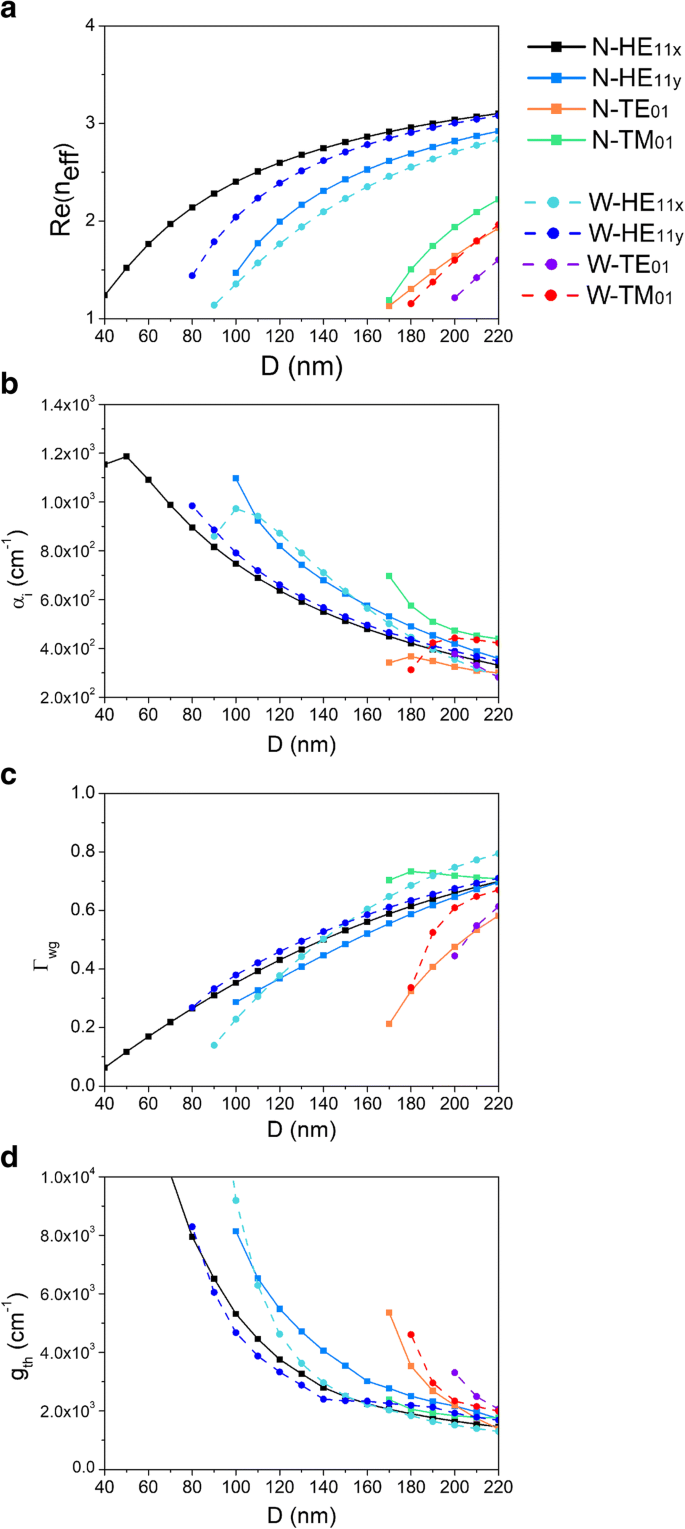
a 的依赖 有效索引的实部，b 模态损失，c 模态限制因子和 d 纳米线直径的阈值增益 D

单位长度的模态损失α 我 和模态限制因子Γ 工作组 是与激光相关的光腔的重要因素。模态限制因子是模式与增益介质重叠程度的指标，其定义为模态增益与有源区域中的材料增益之间的比值 [27, 28]。单位长度的模态损失α 我 可以从模态传播常数k的虚部得到 z 作为 α 我 =2 Im[k z ]。如图 4b 所示，CPN-N 和 CPN-W 激光器的模态损耗与纳米线直径 D 呈负相关 .而如图 4c 所示，CPN-N 和 CPN-W 激光器的限制因子与纳米线直径 D 呈正相关 .随着纳米线直径的减小，电磁能不能很好地集中在纳米线内部，越来越多的电磁能泄漏。部分电磁能量从纳米线上部向外散射，部分能量与凹槽表面相互作用导致更多金属耗散。有趣的是，CPN-N 激光器中的模式 TM01 具有相对较大的限制因子和模态损耗。这可以归因于模式 TM01 的电场分布。如图 3d 所示，电磁能分布在纳米线内部及其表面周围。虽然限制更严，但电磁能与金属凹槽的相互作用更强。重要的是，在图 4c 中，随着纳米线直径的增加，限制因子变大，表明电磁能被限制在腔内并与有源区很好地重叠并可能降低激光阈值。

激射阈值是激光输出受受激发射而非自发发射支配的最低激发水平。阈值增益 g th 描述了激光每单位长度所需的增益，定义为 \( {g}_{\mathrm{th}}=\frac{1}{\varGamma_{wg}}\left[{\alpha}_i+ \frac{1}{L}\ln \left(\frac{1}{R}\right)\right] \)，其中 R 表示纳米线端面反射率的几何平均值，L 是纳米线 F-P 腔的长度 [29]。长度L 固定在 10 μm，符合参考文献中的实验数据。 [12]。需要注意的是，这里的纳米线与Ref相同。 [11, 12]，其中采用了金颗粒催化剂的生长方法。所以，在纳米线的顶部有一个金帽。对于带金帽的端面，反射率比另一端面大，达到70%左右。我们描述了阈值增益 g 的依赖性 第 在 D 在图 4d 中。很明显，阈值增益随着纳米线直径的增加而降低。这符合模态损失和限制因子的行为，它们是阈值增益的关键因素。随着纳米线直径的增加，电磁能被更好地限制在纳米线内部，导致更大的限制因子和更小的能量泄漏损失。因此，阈值增益变低。在较小直径范围内，CPN-N激光器中HE11x模式的阈值增益低于HE11y模式，CPN-W激光器中HE11y模式的阈值增益低于HE11x模式。这也证明了由于凹槽角度对电场分量的影响，HE11x和HE11y模式在CPN激光器中旋转。

品质因数Q 腔模式的能量表示当不存在带间跃迁时该模式的存储能量在腔中保留多长时间，这与光子寿命τ有关 p 通过模式的共振频率 ω 进入速率方程。对于 F-P 腔，品质因数在方法部分 [30] 中定义。高品质因数表示相对于腔体存储的能量而言能量损失率低，并且振荡缓慢消失。因此，该设备可以在较低的阈值下发射激光，因此可以降低泵浦功率。我们描绘了Q 因子作为 D 的函数 在图 5a 中。各模态质量因子与直径D均呈正相关 ，除了 CPN-N 和 CPN-W 激光器中的 TM01 模式。这可以归因于模式 TM01 的电场分布，这在上面已经讨论过。此外，像 CPN 激光器这样的纳米激光器的自发发射率部分取决于光源的环境。根据费米的黄金角色，发射器的自发发射率与局部光态密度 (LDOS) [31] 成正比。在结构处于波长尺度的环境中，LDOS 可以在空间上进行控制 [32]。因此，发射器的 LDOS 可以与自发发射率一起局部增加或通过亚波长微腔降低，这称为珀塞尔效应 [33]。纳米局部电磁能可以通过珀塞尔效应提高自发发射率来降低激光阈值。在 CPN-N 和 CPN-W 激光器中，电磁能量在亚波长范围内被紧密地局部化，导致大的 Purcell 因子，如图 5b 所示。金属凹槽改变了纳米线周围的介电环境并构建了一个亚波长腔，实现了激子和微腔模式之间的超小体积和耦合。随着直径的减小，珀塞尔因子急剧增加，达到100以上。而且，大的LDOS不仅可以提高自发发射率，还可以提高激光作用中的受激发射过程。激光作用可以更容易实现，因为混合等离子体模式的纳米局部电磁场不仅使纳米激光器中的激子快速扩散到更快复合的区域，改善材料增益和等离子体模式之间的重叠，而且还刺激激发态粒子转移能量成具有相同频率、相位和极化的等离子体。为了量化亚波长定位尺度，使用参考文献中的方法计算的归一化模态面积。 [13] 并呈现在图 5c 中。与图5b相比，Purcell因子与归一化模态面积成反比，这证明亚波长尺度的腔增加了Purcell因子，从而提高了自发发射率。

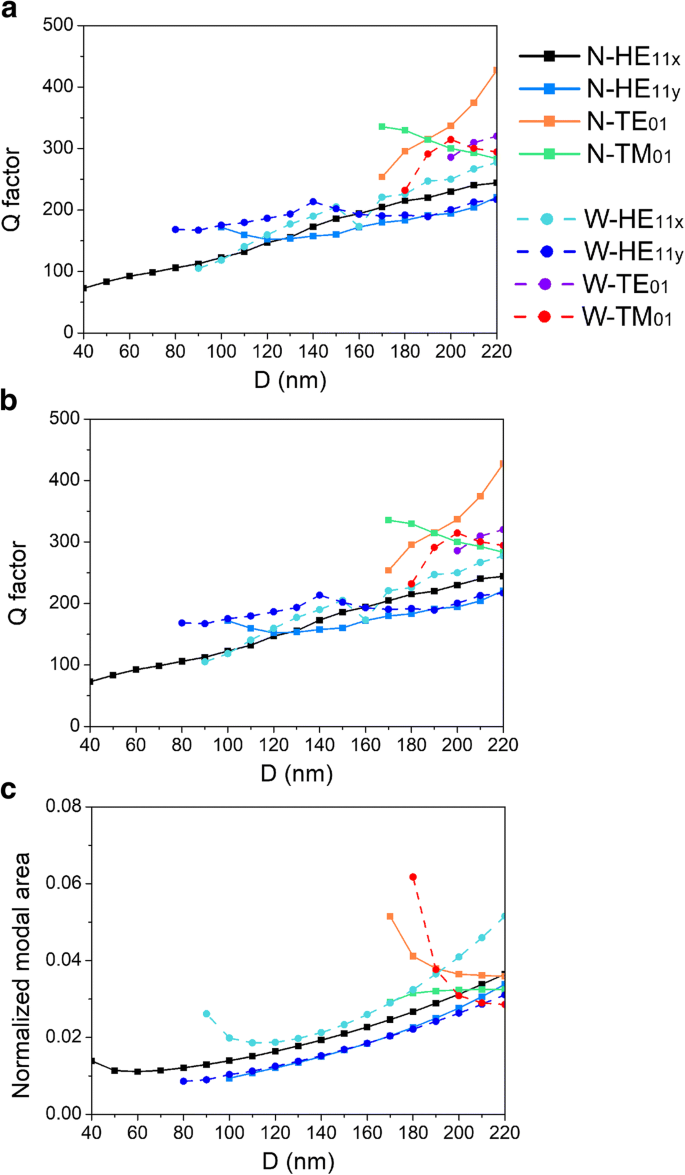
a 的依赖 品质因数，b 珀塞尔因子和c 纳米线直径上的归一化模态面积 D

结论

我们提出了一种基于半导体纳米线和金属 V 型槽以及超薄电介质层的 CPN 激光器结构。随着高指数纳米线的存在，通道等离子体可以以相对大的角度存在于凹槽中，形成混合通道等离子体模式。金属凹槽改变了纳米线周围的介电环境，并构建了一个亚波长腔，能够提高自发发射率。使用有限元方法研究了引导和激光特性。 CPN-N 激光器中的基模 HE11x 具有非常小的截止直径，从而实现了片上激光器的超小尺寸。凭借高约束和超小归一化模态面积的优势，珀塞尔因子可以达到150以上，大大提高了自发发射率。此外，该CPN激光器还具有利用V型槽等离子体波导中的CPP模式与等离子体波导集成的潜在能力，这将在片上光互连中找到重要应用。

方法/实验

使用有限元方法在频率中使用散射边界条件对引导和激光特性进行数值计算，这是模拟必要的开放边界的常用方法。 CPN激光器的本征模电场分布直接通过模式分析获得。引导特性由复传播常数计算，其中β + iα .模态有效指数的实部由n计算 eff =Re(n eff) =β /k 0 , 其中 k 0 是真空波矢。有效模式面积的计算使用[24]

其中 W 米 是总模式能量和 W(r) 是能量密度（沿传播方向流动的每单位长度）。对于色散和有损材料，W(r) 内部可以使用等式计算。 (2):

品质因数和赛尔定义为 [30, 33]

正文中提供了计算模态损失、模态限制因子和阈值增益的方程；此处不再赘述。

缩写

CPN：

通道等离子体纳米线

CPN-N：

通道等离子体纳米线-窄角

CPN-W：

通道等离子体纳米线-广角

CPP：

通道等离子体激元